Sku多維屬性狀態(tài)判斷算法
問題描述
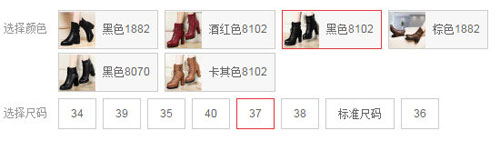
這個(gè)問題來源于選擇商品屬性的場景。比如我們買衣服、鞋子這類物件,一般都需要我們選擇合適的顏色、尺碼等屬性
先了解一下 sku 的學(xué)術(shù)概念吧
最小庫存管理單元(Stock Keeping Unit, SKU)是一個(gè)會(huì)計(jì)學(xué)名詞,定義為庫存管理中的最小可用單元,例如紡織品中一個(gè)SKU通常表示規(guī)格、顏色、款式,而在連鎖零售門店中有時(shí)稱單品為一個(gè)SKU。最小庫存管理單元可以區(qū)分不同商品銷售的最小單元,是科學(xué)管理商品的采購、銷售、物流和財(cái)務(wù)管理以及POS和MIS系統(tǒng)的數(shù)據(jù)統(tǒng)計(jì)的需求,通常對(duì)應(yīng)一個(gè)管理信息系統(tǒng)的編碼。 —— form wikipedia 最小存貨單位
簡單的結(jié)合上面的實(shí)例來說: sku 就是你上購物網(wǎng)站買到的最終商品,對(duì)應(yīng)的上圖中已選擇的屬性是:顏色 黑色 - 尺碼 37
我先看看后端數(shù)據(jù)結(jié)構(gòu)一般是這樣的,一個(gè)線性數(shù)組,每個(gè)元素是一個(gè)描述當(dāng)前 sku 的 map,比如:
- [
- { "顏色": "紅", "尺碼": "大", "型號(hào)": "A", "skuId": "3158054" },
- { "顏色": "白", "尺碼": "中", "型號(hào)": "B", "skuId": "3133859" },
- { "顏色": "藍(lán)", "尺碼": "小", "型號(hào)": "C", "skuId": "3516833" }
- ]
前端展示的時(shí)候顯然需要 group 一下,按不同的屬性分組,目的就是讓用戶按屬性的維度去選擇,group 后的數(shù)據(jù)大概是這樣的:
- {
- "顏色": ["紅", "白", "藍(lán)"],
- "尺碼": ["大", "中", "小"],
- "型號(hào)": ["A", "B", "C"]
- }
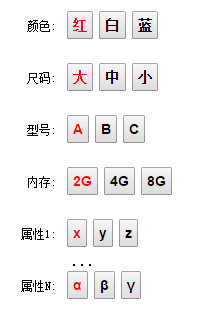
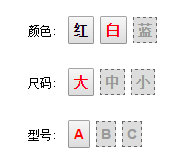
對(duì)應(yīng)的在網(wǎng)頁上大概是這樣的 UI
這個(gè)時(shí)候,就會(huì)有一個(gè)問題,這些元子屬性能組成的集合(用戶的選擇路徑) 遠(yuǎn)遠(yuǎn)大于 真正可以組成的集合,比如上面的屬性集合可以組合成一個(gè) 笛卡爾積,即。可以組合成以下序列:
- [
- ["紅", "大", "A"], // ✔
- ["紅", "大", "B"],
- ["紅", "大", "C"],
- ["紅", "中", "A"],
- ["紅", "中", "B"],
- ["紅", "中", "C"],
- ["紅", "小", "A"],
- ["紅", "小", "B"],
- ["紅", "小", "C"],
- ["白", "大", "A"],
- ["白", "大", "B"],
- ["白", "大", "C"],
- ["白", "中", "A"],
- ["白", "中", "B"], // ✔
- ["白", "中", "C"],
- ["白", "小", "A"],
- ["白", "小", "B"],
- ["白", "小", "C"],
- ["藍(lán)", "大", "A"],
- ["藍(lán)", "大", "B"],
- ["藍(lán)", "大", "C"],
- ["藍(lán)", "中", "A"],
- ["藍(lán)", "中", "B"],
- ["藍(lán)", "中", "C"],
- ["藍(lán)", "小", "A"],
- ["藍(lán)", "小", "B"],
- ["藍(lán)", "小", "C"] // ✔
- ]
根據(jù)公式可以知道,一個(gè)由 3 個(gè)元素,每個(gè)元素是有 3 個(gè)元素的子集構(gòu)成的集合,能組成的笛卡爾積一共有 3 的 3 次冪,也就是 27 種,然而源數(shù)據(jù)只可以形成 3 種組合
這種情況下***能提前判斷出來不可選的路徑并置灰,告訴用戶,否則會(huì)造成誤解
確定規(guī)則
看下圖,如果我們定義紅色為當(dāng)前選中的商品的屬性,即當(dāng)前選中商品為 紅-大-A,這個(gè)時(shí)候如何確認(rèn)其它非已選屬性是否可以組成可選路徑?
規(guī)則是這樣的: 假設(shè)當(dāng)前用戶想選 白-大-A,剛好這個(gè)選擇路徑是不存在的,那么我們就把 白 置灰
以此類推,如果要確認(rèn) 藍(lán) 屬性是否可用,需要查找 藍(lán)-大-A 路徑是否存在
…
解決方法
根據(jù)上面的邏輯代碼實(shí)現(xiàn)思路就有了:
遍歷所有非已選元素:"白", "藍(lán)", "中", "小", "B", "C"遍歷所有屬性行: "顏色", "尺碼", "型號(hào)"取: a) 當(dāng)前元素 b) 非當(dāng)前元素所在的其它屬性已選元素,形成一個(gè)路徑
- 判斷此路徑是否存在,如果不存在將當(dāng)前元素置灰
a.看來問題似乎已經(jīng)解決了,然而 …
我們忽略了一個(gè)非常重要的問題:上例中雖然 白 元素置灰,但是實(shí)際上 白 是可以被點(diǎn)擊的!因?yàn)橛脩艨梢赃x擇 白-中-B 路徑
如果用戶點(diǎn)擊了 白 情況就變得復(fù)雜了很多,我們假設(shè)用戶 只選擇了一個(gè)元素 白,此時(shí)如何判斷其它未選元素是否可選?
即:如何確定 "大", "中", "小", "A", "B", "C" 需要置灰? 注意我們并不需要確認(rèn) "紅","藍(lán)"是否可選,因?yàn)閷傩岳锩娴脑囟际? 單選,當(dāng)前的屬性里任何元素都可選的
縮小問題規(guī)模
我們先 縮小問題范圍:當(dāng)前情況下(只有一個(gè) 白 已選)如何確定尺碼 "大" 需要置灰? 你可能會(huì)想到根據(jù)我們之間的邏輯,需要分別查找:
- 白 - 大 - A
- 白 - 大 - B
- 白 - 大 - C
他們都不存在的時(shí)候把尺碼 大 置灰,問題似乎也可以解決。其實(shí)這樣是不對(duì)的,因?yàn)?型號(hào)沒有被選擇過,所以只需要知道 白-大是否可選即可
同時(shí)還有一個(gè)問題,如果已選的個(gè)數(shù)不確定而且維度可以增加到不確定呢?
這種情況下如果還按之前的算法,即使實(shí)現(xiàn)也非常復(fù)雜。這時(shí)候就要考慮換一種思維方式
調(diào)整思路
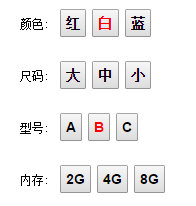
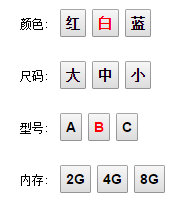
之前我們都是反向思考,找出不可選應(yīng)該置灰的元素。我們現(xiàn)在正向的考慮,如何確定屬性是否可選。而且多維的情況下用戶可以跳著選。比如:用戶選了兩個(gè)元素 白,B
圖1
我們再回過頭來看下 原始存在的數(shù)據(jù)
- [
- { "顏色": "紅", "尺碼": "大", "型號(hào)": "A", "skuId": "3158054" },
- { "顏色": "白", "尺碼": "中", "型號(hào)": "B", "skuId": "3133859" },
- { "顏色": "藍(lán)", "尺碼": "小", "型號(hào)": "C", "skuId": "3516833" }
- ]
- // 即
- [
- [ "紅", "大", "A" ], // 存在
- [ "白", "中", "B" ], // 存在
- [ "藍(lán)", "小", "C" ] // 存在
- ]
顯然:如果***條數(shù)據(jù) "紅", "大", "A" 存在,那么下面這些子組合 肯定都存在:
- 紅
- 大
- A
- 紅 - 大
- 紅 - A
- 大 - A
- 紅 - 大 - A
同理:如果第二條數(shù)據(jù) "白", "中", "B" 存在,那么下面這些子組合 肯定都存在:
- 白
- 中
- B
- 白 - 中
- 白 - B
- 中 - B
- 白 - 中 - B
…
我們提前把 所有存在的路徑中的子組合 算出來,算法上叫取集合所有子集,數(shù)學(xué)上叫 冪集, 形成一個(gè)所有存在的路徑表,算法如下:
- /**
- * 取得集合的所有子集「冪集」
- arr = [1,2,3]
- i = 0, ps = [[]]:
- j = 0; j < ps.length => j < 1:
- i=0, j=0 ps.push(ps[0].concat(arr[0])) => ps.push([].concat(1)) => [1]
- ps = [[], [1]]
- i = 1, ps = [[], [1]] :
- j = 0; j < ps.length => j < 2
- i=1, j=0 ps.push(ps[0].concat(arr[1])) => ps.push([].concat(2)) => [2]
- i=1, j=1 ps.push(ps[1].concat(arr[1])) => ps.push([1].concat(2)) => [1,2]
- ps = [[], [1], [2], [1,2]]
- i = 2, ps = [[], [1], [2], [1,2]]
- j = 0; j < ps.length => j < 4
- i=2, j=0 ps.push(ps[0].concat(arr[2])) => ps.push([3]) => [3]
- i=2, j=1 ps.push(ps[1].concat(arr[2])) => ps.push([1, 3]) => [1, 3]
- i=2, j=2 ps.push(ps[2].concat(arr[2])) => ps.push([2, 3]) => [2, 3]
- i=2, j=3 ps.push(ps[3].concat(arr[2])) => ps.push([2, 3]) => [1, 2, 3]
- ps = [[], [1], [2], [1,2], [3], [1, 3], [2, 3], [1, 2, 3]]
- */
- function powerset(arr) {
- var ps = [[]];
- for (var i=0; i < arr.length; i++) {
- for (var j = 0, len = ps.length; j < len; j++) {
- ps.push(ps[j].concat(arr[i]));
- }
- }
- return ps;
- }
有了這個(gè)存在的子集集合,再回頭看 圖1 舉例:
圖1
- 如何確定 紅 可選? 只需要確定 紅-B 可選
- 如何確定 中 可選? 需要確定 白-中-B 可選
- 如何確定 2G 可選? 需要確定 白-B-2G 可選
算法描述如下:
- 遍歷所有非已選元素
a.遍歷所有屬性行
取: a) 當(dāng)前元素 b) 非當(dāng)前元素所在的其它屬性已選元素(如果當(dāng)前屬性中沒已選元素,則跳過),形成一個(gè)路徑
判斷此路徑是否存在(在所有存在的路徑表中查詢),如果不存在將當(dāng)前元素置灰
以最開始的后端數(shù)據(jù)為例,生成的所有可選路徑表如下: 注意路徑用分割符號(hào)「-」分開是為了查找路徑時(shí)方便,不用遍歷
- {
- "": {
- "skus": ["3158054", "3133859", "3516833"]
- },
- "紅": {
- "skus": ["3158054"]
- },
- "大": {
- "skus": ["3158054"]
- },
- "紅-大": {
- "skus": ["3158054"]
- },
- "A": {
- "skus": ["3158054"]
- },
- "紅-A": {
- "skus": ["3158054"]
- },
- "大-A": {
- "skus": ["3158054"]
- },
- "紅-大-A": {
- "skus": ["3158054"]
- },
- "白": {
- "skus": ["3133859"]
- },
- "中": {
- "skus": ["3133859"]
- },
- "白-中": {
- "skus": ["3133859"]
- },
- "B": {
- "skus": ["3133859"]
- },
- "白-B": {
- "skus": ["3133859"]
- },
- "中-B": {
- "skus": ["3133859"]
- },
- "白-中-B": {
- "skus": ["3133859"]
- },
- "藍(lán)": {
- "skus": ["3516833"]
- },
- "小": {
- "skus": ["3516833"]
- },
- "藍(lán)-小": {
- "skus": ["3516833"]
- },
- "C": {
- "skus": ["3516833"]
- },
- "藍(lán)-C": {
- "skus": ["3516833"]
- },
- "小-C": {
- "skus": ["3516833"]
- },
- "藍(lán)-小-C": {
- "skus": ["3516833"]
- }
- }
為了更清楚的說明這個(gè)算法,再上一張圖來解釋下吧:
所以根據(jù)上面的邏輯得出,計(jì)算狀態(tài)后的界面應(yīng)該是這樣的:
現(xiàn)在這種情況下如果用戶點(diǎn)擊 尺碼 中 應(yīng)該怎么交互呢?
優(yōu)化體驗(yàn)
因?yàn)楫?dāng)前情況下路徑 紅-中-A 并不存在,如果點(diǎn)擊 中,那么除了尺碼 中 之外其它的屬性中 至少有一個(gè) 屬性和 中 的路徑搭配是不存在的
交互方面需求是:如果不存在就高亮當(dāng)前屬性行,使用戶必須選擇到可以和 中 組合存在的屬性。而且用戶之間選擇過的屬性要做一次緩存
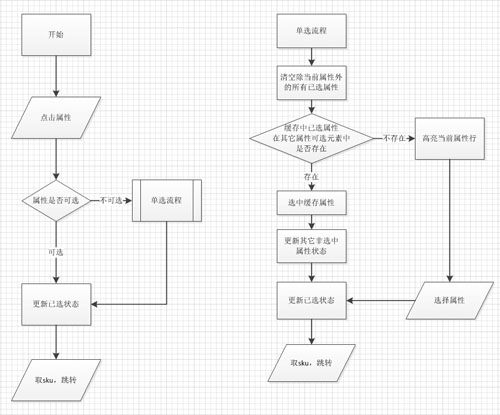
所以當(dāng)點(diǎn)擊不存在的屬性時(shí)交互流程是這樣的:
- 無論當(dāng)前屬性存不存在,先高亮(選中)當(dāng)前屬性
- 清除其它所有已選屬性
- 更新當(dāng)前狀態(tài)(只選當(dāng)前屬性)下的其它屬性可選狀態(tài)
- 遍歷非當(dāng)前屬性行的其它屬性查找對(duì)應(yīng)的在緩存中的已選屬性
- 如果緩存中對(duì)應(yīng)的屬性存在(可選),則默認(rèn)選中緩存屬性并 再次更新 其它可選狀態(tài)。不存在,則高亮當(dāng)前屬性行(深色背景)
這個(gè)過程的流程圖大概是這樣的,點(diǎn)進(jìn)不存在的屬性就會(huì)進(jìn)入「單選流程」
假設(shè)后端數(shù)據(jù)是這樣的:
- [
- { "顏色": "紅", "尺碼": "大", "型號(hào)": "A", "skuId": "3158054" },
- { "顏色": "白", "尺碼": "大", "型號(hào)": "A", "skuId": "3158054" }, // 多加了一條
- { "顏色": "白", "尺碼": "中", "型號(hào)": "B", "skuId": "3133859" },
- { "顏色": "藍(lán)", "尺碼": "小", "型號(hào)": "C", "skuId": "3516833" }
- ]
當(dāng)前選中狀態(tài)是:白-大-A
如果用戶點(diǎn)擊 中。這個(gè)時(shí)候 白-中 是存在的,但是 中-A 并不存在,所以保留顏色 白,高亮型號(hào)屬性行:
由此可見和 白-中 能搭配存在型號(hào)只有 B,而緩存的作用就是為了少讓用戶選一次顏色 白到這里,基本上主要的功能就實(shí)現(xiàn)了。比如庫存邏輯處理方式也和不存屬性一樣,就不再贅述。唯一需要注意的地方是求冪集的復(fù)雜度問題
算法復(fù)雜度
冪集算法的時(shí)間復(fù)雜度是 O(2^n),也就是說每條數(shù)據(jù)上面的屬性(維度)越多,復(fù)雜度越高。sku 數(shù)據(jù)的多少并不重要,因?yàn)槭浅?shù)級(jí)的線性增長,而維度是指數(shù)級(jí)的增長
- {1} 2^1 = 2
- => {},{1}
- {1,2} 2^2 = 4
- => {},{1},{2},{1,2}
- {1,2,3} 2^3 = 8
- => {},{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}
- ...
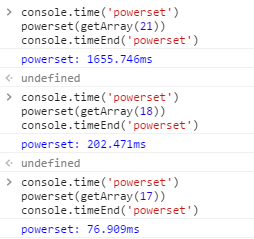
在 chrome 里面簡單跑了幾個(gè)用例,可見這個(gè)算法非常低效,如果要使用這個(gè)算法,必須控制維度在合理范圍內(nèi),而且不僅僅算法時(shí)間復(fù)雜度很高,生成***的路徑表也會(huì)非常大,相應(yīng)的占用內(nèi)存也很高。
舉個(gè)例子:如果有一個(gè) 10 維的 sku,那么最終生成的路徑表會(huì)有 2^10 個(gè)(1024) key/value
最終 demo 可以查看這個(gè): sku 多維屬性狀態(tài)判斷
相關(guān)資料: sku組合查詢算法探索
【本文是51CTO專欄作者周琪力的原創(chuàng)稿件,轉(zhuǎn)載請注明出處】