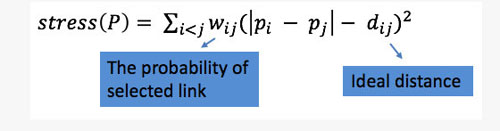[[183284]]

不確定網絡，在本文表示頂點是確定的(certain)，邊的存在與否滿足某種概率分布的網絡。在圖1中，左圖是確定網絡(certain graph)，右圖是不確定網絡(uncertain graph)。

在不確定網絡可視分析中，現有的方法往往直接在確定圖(exact graph)中用視覺變量(visual variables)表示不確定信息。這些方法可以很好的將圖的拓撲結構展示出來，但忽略了不確定信息的概率分布情況。

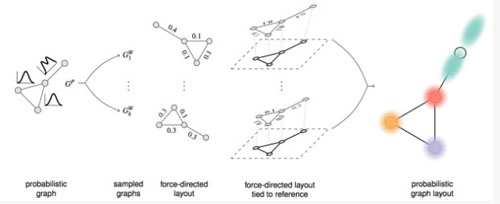
在這篇文章[1]，作者們提出一個概率圖(probabilistic graph)布局方法。這個方法可以同時展示圖的拓撲結構和不確定信息的概率分布。它的基本思想是，依據蒙特卡洛方法(Monte Carlo process)對不確定圖進行采樣;將采樣獲得圖根據力導向算法進行布局;之后，將所有采樣圖的力導向布局組合起來，獲得***概率圖的布局(如圖2所示)。

圖1 左圖是確定圖;右圖是不確定圖

圖2 文章提出的概率圖布局方法流程圖

文章分析的數據可以用G = (V, E, F)表示，其中V表示頂點集合。頂點是確定的元素;E表示邊集合。邊的存在與否滿足F表示的概率密度函數。

在采樣階段，采用隨機采樣方法。

在力導向布局階段，他們采用圖3公式優化圖布局。其中dij表示頂點i和頂點j之間的理想距離;wij表示邊被選取的概率。

圖3 力導向算法優化函數

在組合階段，目標是將所有采樣圖的力導向布局整合成一個布局。文章提出的方法是構建一個參考布局(reference layout)，然后將所有的采樣圖根據圖4公式，重新布局。

圖4 根據參考布局，重新布局的優化函數

在文中，參考布局一般是期望圖(expected graph)。在期望圖中，邊的權重是該邊概率分布的期望值。

在可視化階段，為了更好的將每個頂點的位置分布情況和整體的圖結構展示出來，他們對***計算得到的整合布局進行了一系列的處理。

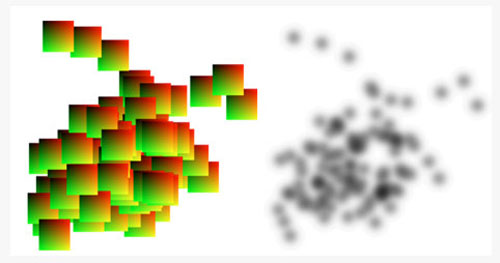
首先，他們對圖中的頂點進行了滾雪球(splatting)處理。這樣處理的目的是為了更好的將相同頂點的可能位置展示出來。在實際處理中，他們采用核密度估計函數計算每個頂點位置的概率密度分布函數，然后用ray-casting的方法，將頂點的位置分布展現出來(圖5)。在核密度估計函數中，帶寬h的值對結果的影響很大。圖6展示了在不同h的情況，獲取的結果。從左至右，布局從欠平滑狀態過渡到過平滑狀態。文章作者認為欠平滑的布局更利于用戶進一步的分析，因為欠平滑的布局可以清晰展現頂點和邊的關系。

圖5

左圖每個方塊表示每個頂點位置的概率密度分布;右圖是在左圖基礎上進行ray-casting后得到的布局

圖6 從左至右，布局從欠平滑狀態過渡到過平滑狀態

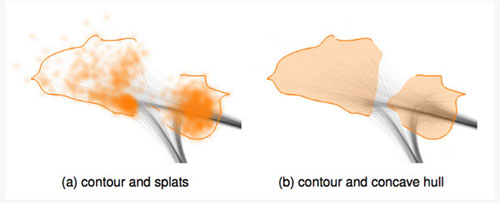
接著，他們對***計算得到的整合圖中的邊進行了處理。為了更好的描述邊的分布和圖的拓撲結構，他們對圖中的邊進行了層次聚類;接著采用貝賽爾曲線表示這些邊，并采用滾雪球的方法對邊進行可視化(圖7)。

圖7 左圖，直接用直線展示邊的布局;右圖，對邊進行一系列處理后的布局

***，他們采用Welsh-Powell方法對圖中的頂點進行著色。因為同個頂點的位置分布可能因為一些異常值，導致在空間上不能聚集在一起。為了幫助用戶快速的識別同個頂點的位置分布，他們對圖中的頂點進行了聚類處理。針對每個聚類，他們計算了群簇的邊緣，并將表示同個頂點的群簇通過圖8的方法，連接起來。

圖8 對頂點進行聚類，添加邊緣的結果

根據輪廓之間的空缺方向，用戶可以將屬于同個頂點的群簇鏈接起來。

接下來，我將介紹兩個實例，驗證這個方法的可用性。

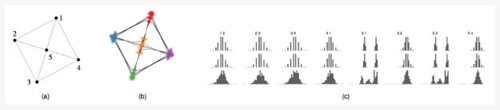
***個例子使用的是人造數據。在這個數據中，有五個頂點，8條邊。每條邊的概率分布如圖9(c)***行所示。圖9(a)表示的是這個人造數據的期望圖。我們可以發現，這個布局可以清晰的展示圖的拓撲結構，但不能將邊的不確定信息展示出來;圖9(b)表示的是通過文章的方法計算得到的布局。

它清晰的展現了圖的拓撲結構和頂點的位置分布;圖9(c)表示的是邊的統計信息。每一列表示一條邊，***行表示邊存在與否的概率分布，第二行表示采樣獲得的邊的概率分布，第三行表示邊的歐拉距離分布。我們可以發現，同一列的三個分布都非常的相似。這說明，足夠的采樣是可以逼近真實概率分布的;也說明他們的方法可以很好的將圖拓撲結構展現出來。

圖9 (a)期望圖;(b)根據文章的方法得到的布局;(c)邊的統計信息分布圖

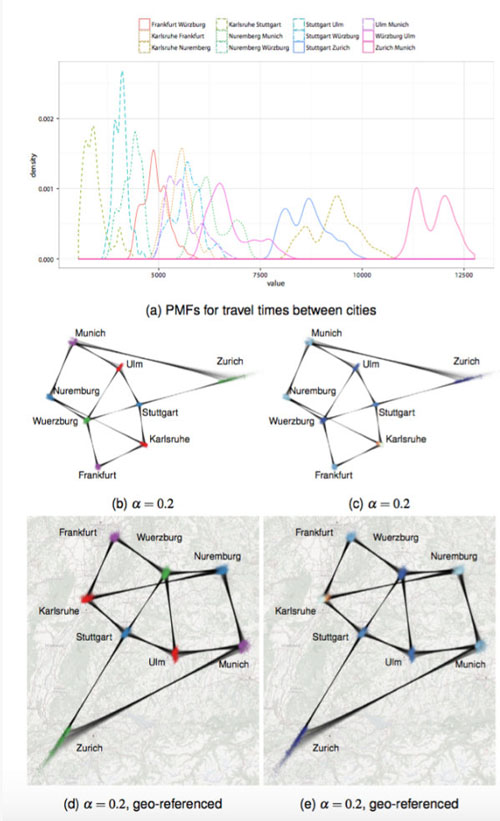
在第二個例子中，他們嘗試用這個方法分析城市之間的行程時間。該例子分析了8個城市之間的行程時間。在構圖上，他們將每個城市看作頂點，在可到達的城市之間建立邊。邊的權重表示行程時間。為獲取城市之間的行程時間，他們通過Google Direction API隨機獲取不同時間段，任意兩個連接的城市之間的行程時間，并通過直方圖處理，獲取城市之間行程時間的概率分布圖(如圖10(a)所示)。

接著，他們根據不同的參考布局，得到了不同的概率圖布局。圖10(b)和(c)展示的布局，在其參考布局中，頂點的位置是不確定的，但頂點之間的理想距離是相應城市之間的真實距離。圖10(d)和(e)展示的布局，在其參考布局中，頂點的位置就是相應城市的地理位置。我們可以發現，這兩類參考布局得到的***布局非常的相似，它們似乎只是旋轉了不同的角度。

圖10 (a)城市之間行程時間的概率分布圖;(b)(c)和(d)(e)是兩種參考布局得到的概率圖布局

總的來說，這篇文章提出了一個新穎的不確定網絡的可視化方法。他們的方法可以清晰的展現圖的拓撲結構和圖中不確定信息的概率分布。