本文旨在提供直觀簡明的深度學習引導，涵蓋深度學習的基本概念，而不涉及很多數學和理論細節。當然如果要做更深入的研究，數學肯定是必不可少的，但是本系列主要還是用圖片和類比等方式，幫助初學者快速建立大局觀。

核心概念

機器學習(Machine Learning)

在機器學習中，我們(1)讀取數據，(2)訓練模型，(3)使用模型對新數據做預測。訓練可以看作是當模型拿到新數據的時候、逐步學習一個的過程。在每一步，模型做出預測并且得到準確度的反饋。反饋的形式即是某種衡量標準(比如與正確解的距離)下的誤差，再被用于修正預測誤差。

學習是一個在參數空間里循環往復的過程：當你調整參數改正一次預測，但是模型卻可能把原先對的又搞錯了。需要很多次的迭代，模型才能具有良好的預測能力，這一“預測-修正”的過程一直持續到模型再無改良空間。

特征工程(Feature Engineering)

特征工程從數據中提取有用的模式，使之更容易被機器學習模型進行分類。比如，把一堆綠色或藍色的像素區域作為標準，來判斷照片上是陸生動物還是水生動物。這一特征對于機器學習模型十分有效，因為其限制了需要考慮的類別數量。

在多數預測任務中，特征工程是取得好結果的必備技能。然而，因為不同的數據集有著不同的特征工程方法，所以很難得出普遍規律，只有一些大概的經驗，這使得特征工程更是一門藝術而非科學。一個數據集里極其關鍵的特征，到了另一個數據集里可能沒有卵用(比如下一個數據集里全是植物)。正因為特征工程這么難，才會有科學家去研發自動提取特征的算法。

很多任務已經可以自動化(比如物體識別、語音識別)，特征工程還是復雜任務中最有效的技術(比如Kaggle機器學習競賽中的大多數任務)。

特征學習(Feature Learning)

特征學習算法尋找同類之間的共有模式，并自動提取用以分類或回歸。特征學習就是由算法自動完成的特征工程。在深度學習中，卷積層就極其擅長尋找圖片中的特征，并映射到下一層，形成非線性特征的層級結構，復雜度逐漸提升(例如：圓圈，邊緣 -> 鼻子，眼睛，臉頰)。最后一層使用所有生成的特征來進行分類或回歸(卷積網絡的最后一層，本質上就是多項式邏輯回歸)。

圖1：深度學習算法學得的層級特征。  

每個特征都相當于一個濾波器，

用特征(比如鼻子)去過濾輸入圖片。

如果這個特征找到了，相應的單元就會產生高激勵，

在之后的分類階段中，就是此類別存在的高指標。

圖1顯示了深度學習算法生成的特征，很難得的是，這些特征意義都很明確，因為大多數特征往往不知所云，特別是循環神經網絡、LSTM或特別深的深度卷積網絡。

深度學習(Deep Learning)

在層級特征學習中，我們提取出了好幾層的非線性特征，并傳遞給分類器，分類器整合所有特征做出預測。我們有意堆疊這些深層的非線性特征，因為層數少了，學不出復雜特征。數學上可以證明，單層神經網絡所能學習的最好特征，就是圓圈和邊緣，因為它們包含了單個非線性變換所能承載的最多信息。為了生成信息量更大的特征，我們不能直接操作這些輸入，而要對第一批特征(邊緣和圓圈)繼續進行變換，以得到更復雜的特征。

研究顯示，人腦有著相同的工作機理：視錐細胞接受信息的第一層神經，對邊緣和圓圈更加敏感，而更深處的大腦皮層則對更加復雜的結構敏感，比如人臉。

層級特征學習誕生在深度學習之前，其結構面臨很多嚴重問題，比如梯度消失——梯度在很深的層級處變得太小，以致于不能提供什么學習信息了。這使得層級結構反而表現不如一些傳統機器學習算法(比如支持向量機)。

為解決梯度消失問題，以便我們能夠訓練幾十層的非線性層及特征，很多新的方法和策略應運而生，“深度學習”這個詞就來自于此。在2010年代早期，研究發現在GPU的幫助下，激勵函數擁有足以訓練出深層結構的梯度流，從此深度學習開始了穩步發展。

深度學習并非總是與深度非線性層級特征綁定，有時也與序列數據中的長期非線性時間依賴相關。對于序列數據，多數其他算法只有最后10個時間步的記憶，而LSTM循環神經網絡(1997年由Sepp Hochreiter和Jürgen Schmidhuber發明)，使網絡能夠追溯上百個時間步之前的活動以做出正確預測。盡管LSTM曾被雪藏將近10年，但自從2013年與卷積網絡結合以來，其應用飛速成長。

基本概念

邏輯回歸(Logistic Regression)

回歸分析預測統計輸入變量之間的關系，以預測輸出變量。邏輯回歸用輸入變量，在有限個輸類別變量中產生輸出，比如“得癌了” / “沒得癌”，或者圖片的種類如“鳥” / “車” / “狗” / “貓” / “馬”。

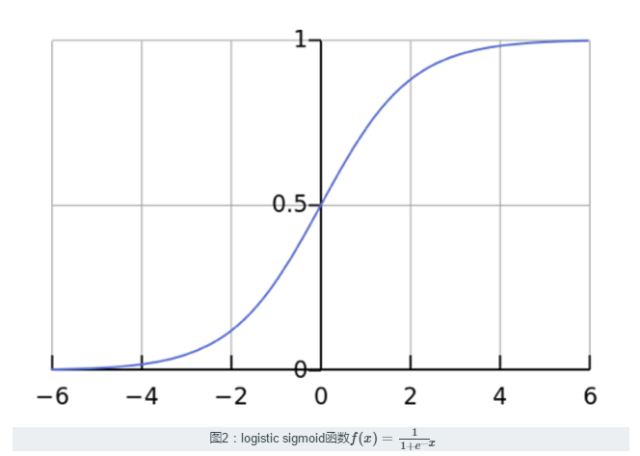
邏輯回歸使用logistic sigmoid函數(見圖2)給輸入值賦予權重，產生二分類的預測(多項式邏輯回歸中，則是多分類)。

邏輯回歸與非線性感知機或沒有隱藏層的神經網絡很像。主要區別在于，只要輸入變量滿足一些統計性質，邏輯回歸就很易于解釋而且可靠。如果這些統計性質成立，只需很少的輸入數據，就能產生很穩的模型。因而邏輯回歸在很多數據稀疏的應用中，具有極高價值。比如醫藥或社會科學，邏輯回歸被用來分析和解釋實驗結果。因為邏輯回歸簡單、快速，所以對大數據集也很友好。

在深度學習中，用于分類的神經網絡中，最后幾層一般就是邏輯回歸。本系列將深度學習算法看作若干特征學習階段，然后將特征傳遞給邏輯回歸，對分類進行輸入。

人工神經網絡(Aritificial Neural Network)

人工神經網絡(1)讀取輸入數據，(2)做計算加權和的變換，(3)對變換結果應用非線性函數，計算出一個中間狀態。這三步合起來稱為一“層”，變換函數則稱為一個“單元”。中間狀態——特征——也是另一層的輸入。

通過這些步驟的重復，人工神經網絡學的了很多層的非線性特征，最后再組合起來得出一個預測。神經網絡的學習過程是產生誤差信號——網絡預測與期望值的差——再用這些誤差調整權重(或其他參數)使預測結果更加準確。

Kaiser：以下為幾個名詞的辨析，包括最近幾年的習慣變遷，我認為不需要深究。

單元(Unit)

單元有時指一層中的激勵函數，輸入正是經由這些非線性激勵函數進行變換，比如logistic sigmoid函數。通常一個單元會連接若干輸入和多個輸出，也有更加復雜的，比如長短期記憶(LSTM)單元就包含多個激勵函數，并以特別的布局連接到非線性函數，或最大輸出單元。LSTM經過對輸入的一系列非線性變換，計算最終的輸出。池化，卷積及其他輸入變換函數一般不稱作單元。

人工神經元(Artificial Neuron)

人工神經元——或神經元——與“單元”是同義詞，只不過是為了表現出與神經生物學和人腦的緊密聯系。實際上深度學習和大腦沒有太大關系，比如現在認為，一個生物神經元更像是一整個多層感知機，而不是單個人工神經元。神經元是在上一次AI寒冬時期被提出來的，目的是將最成功的神經網絡與失敗棄置的感知機區別開來。不過自從2012年以后深度學習的巨大成功以來，媒體經常拿“神經元”這個詞來說事兒，并把深度學習比作人腦的擬態。這其實是具有誤導性，對深度學習領域來講也是危險的。如今業界不推薦使用“神經元”這個詞，而改用更準確的“單元”。

激勵函數(Acitivation Function)

激勵函數讀取加權數據(輸入數據和權重進行矩陣乘法)，輸出數據的非線性變換。比如output = max(0, weight_{data})就是修正線性激勵函數(本質上就是把負值變成0)。“單元”和“激勵函數”之間的區別是，單元可以更加復雜，比如一個單元可以包含若干個激勵函數(就像LSTM單元)或者更復雜的結構(比如Maxout單元)。

Kaiser：原文這個例子顯然把簡單的問題說復雜了，建議跳過。

線性激勵函數，與非線性激勵函數的區別，可以通過一組加權值之間的關系體現：想象4個點A1, A2, B1, B2。點(A1 / A2)，和(B1 / B2)很接近，但是A1和B1, B2都很遠，A2亦然。

經過線性變換，點之間的關系會變化，比如A1和A2遠離了，但同時B1和B2也遠離了。但是(A1 / A2)和(B1 / B2)的關系不變。

而非線性變換則不同，我們可以增加A1和A2的距離，同時減小B1和B2的距離，如此就建立了復雜度更高的新關系。在深度學習中，每一次層的非線性激勵函數都創造了更復雜的特征。

而純線性變換，哪怕有1000層，也可以用一個單層來表示(因為一連串的矩陣相乘可以用一個矩陣乘法來表示)。這就是為什么非線性激勵函數在深度學習中如此重要。

層(Layer)

層是深度學習更高級的基本構成單位。一層，就是接受加權輸入、經過非線性激勵函數變換、作為輸出傳遞給下一層的容器。一層通常只含一種激勵函數，池化、卷積等等，所以可以簡單地與網絡其他部分作對比。第一層和最后一層分別稱為“輸入層”和“輸出層”，中間的都稱作“隱藏層”。

卷積深度學習

卷積(Convolution)

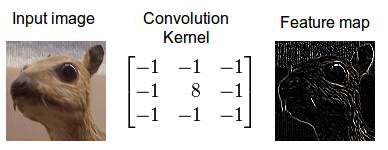
卷積是一種數學操作，表述了混合兩個函數或兩塊信息的規則：(1)特征映射或輸入數據嗎，與(2)卷積核混合，形成(3)變換特征映射。卷積也經常被當做是一種濾波器，卷積核(kernel)過濾特征映射以找到某種信息，比如一個卷積核可能是只找邊緣，而拋掉其他信息。

圖3：用邊緣檢測卷積核，對圖像進行卷積操作。

卷積在物理和數學中都很重要，因為他建立了時域和空間(位置(0,30)的，像素值147)以及頻域(幅度0.3，頻率30Hz，相位60度)的橋梁。這一橋梁的建立是通過傅里葉變換：當你對卷積核與特征映射都做傅里葉變換時，卷積操作就被極大簡化了(積分變成了相乘)。

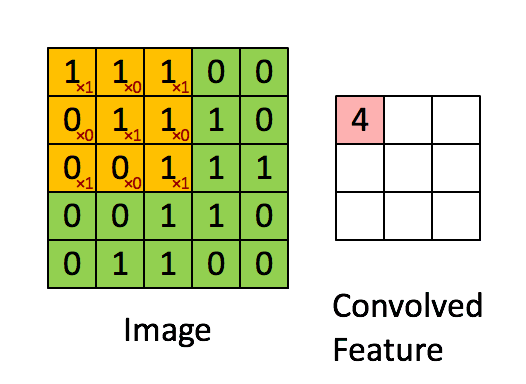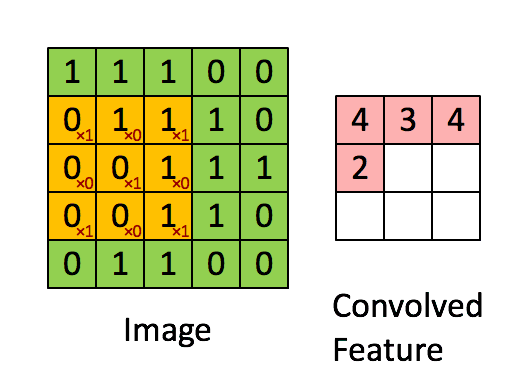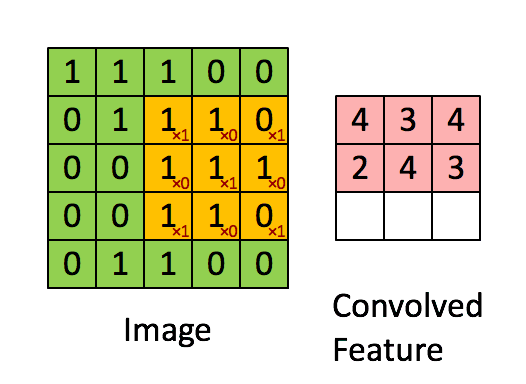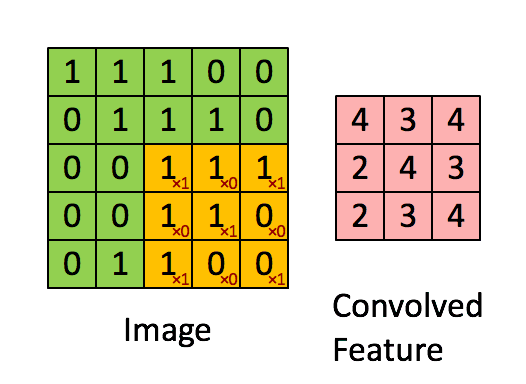
圖4：用圖像窗在整個圖像上滑動計算卷積。

原始圖像(綠色)的圖像窗(黃色)

與卷積核(紅字)相乘再相加，

得到特征映射中的一個向量

(Convolved Feature里的粉紅單元)。

卷積，可以描述信息的擴散。比如當你把牛奶倒進咖啡卻不攪拌，這是擴散就發生了，而且可以通過卷積精確描述(像素向著圖像邊緣擴散)。在量子力學當中，這描述了當你測量一個量子的位置時，其在特定位置出現的概率(像素在邊緣處于最高位置的概率)。在概率論中，者描述了互相關，也就是兩個序列的相似度(如果一個特征(如鼻子)里的像素，與一個圖像(比如臉)重疊，那么相似度就高)。在統計學中，卷積描述了正太輸入血獵的加權動平均(邊緣權重高，其他地方權重低)。另有其它很多不同角度的解釋。

Kaiser：這里的“邊緣”不同于之前的edge，原詞為contour，指決策邊界。比如對于人臉識別，人臉的輪廓就是contour，識別的重點。

不過對于深度學習，我們也不知道卷積的哪一種解釋才是正確的，互相關(cross-correlation)解釋是目前最有效的：卷積濾波器是特征檢測器，輸入(特征映射)被某個特征(kernel)所過濾，如果該特征被檢測到了，那么輸出就高。這也是圖像處理中互相關的解釋。

圖5： 圖像的互相關。

卷積核上下倒過來，就是互相關了。

核Kernel可以解釋為特征檢測器，

如果檢測到了，就會產生高輸出(白色)，

反之則為低輸出(黑色)。

池化/下采樣(Pooling/Sub-Sampling)

池化過程從特定區域讀取輸入，并壓縮為一個值(下采樣)。在卷積神經網絡中，信息的集中是種很有用的性質，這樣輸出連接通常接收的都是相似信息(信息像經過漏斗一樣，流向對應下一個卷積層的正確位置)。這提供了基本的旋轉/平移不變性。比如，如果臉不在圖片的中心位置，而是略有偏移，這應該不影響識別，因為池化操作將信息導入到了正確位置，故卷積濾波器仍能檢測到臉。

池化區域越大，信息壓縮就越多，從而產生更“苗條”的網絡，也更容易配合顯存。但是如果池化面積太大，丟失信息太多，也會降低預測能力。

Kaiser：以下部分將之前羅列的概念串了起來，是全文的精華所在。

卷積神經網絡(Convolutional Neural Network, CNN)

卷積神經網絡，或卷積網絡，使用卷積層過濾輸入以獲得有效信息。卷積層有的參數是自動學習獲得的，濾波器自動調整以提取最有用的信息(特征學習)。比如對于一個普適的物體識別任務，物體的形狀可能是最有用的;而對于鳥類識別人物，顏色可能是最有用的(因為鳥的形狀都差不多，而顏色卻五花八門)。

一般我們使用多個卷積層過濾圖像，每一層之后獲得的信息，都越來越抽象(層級特征)。

卷積網絡使用池化層，獲得有限的平移/旋轉不變性(即使目標不在通常位置，也能檢測出來)。池化也降低了內存消耗，從而能夠使用更多卷積層。

最近的卷積網絡使用inception模塊，即1x1的卷積核進一步降低內存消耗，加速計算和訓練過程。

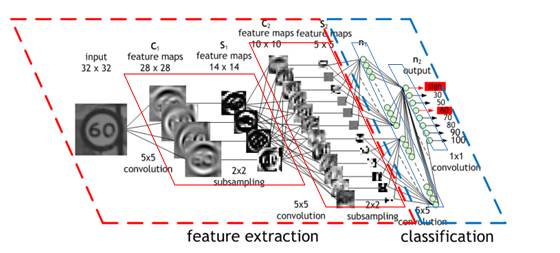
圖6：一個交通標志圖像被4個5x5卷積核濾波，

生成了4個特征映射，這些特征映射經過“最大池化”。

下一層對之前下采樣過的圖像應用10個5x5卷積核，

并在此池化。

最后一層是全連接層，

所有的特征都組合起來傳遞給分類器(本質上就是邏輯回歸)。

Inception

卷積網絡中，inception模塊的設計初衷是為了以更高的計算效率，執行更深、更大的卷積層。Inception使用1x1的卷積核，生成很小的特征映射。比如192個28x28的特征映射，可以經過64個1x1的卷積，被壓縮成64個28x28的特征映射。因為尺寸縮小了，這些1x1的卷積后面還可以跟跟大的卷積，比如3x3，5x5。除了1x1卷積，最大池化也用來降維。

Inception模塊的輸出，所有的大卷積都拼接成一個大的特征映射，再傳遞給下一層(或inception模塊)。