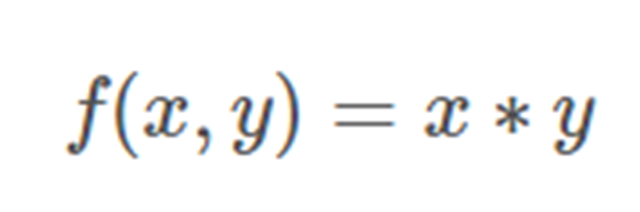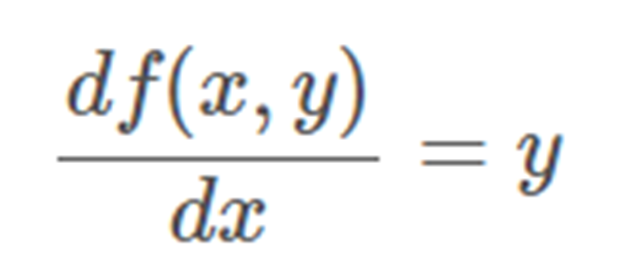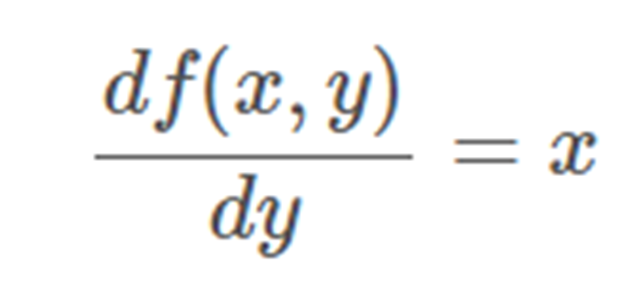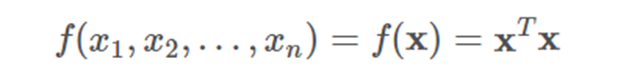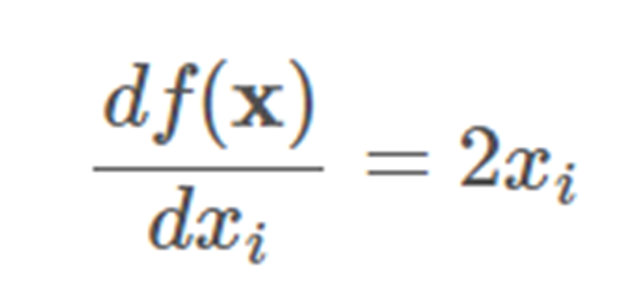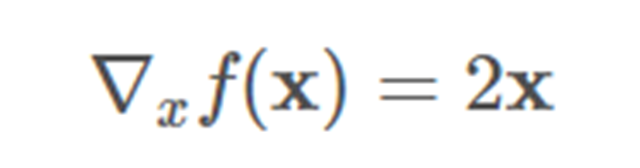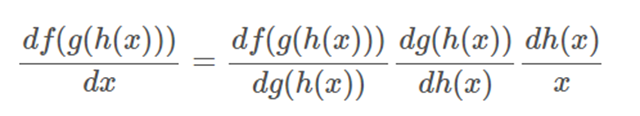如何利用C++搭建個人專屬的TensorFlow
在開始之前,首先看一下最終成型的代碼:
1. 分支與特征后端(https://github.com/OneRaynyDay/autodiff/tree/eigen)
2. 僅支持標(biāo)量的分支(https://github.com/OneRaynyDay/autodiff/tree/master)
這個項目是我與 Minh Le 一起完成的。
為什么?
如果你修習(xí)的是計算機科學(xué)(CS)的人的話,你可能聽說過這個短語「不要自己動手____」幾千次了。它包含了加密、標(biāo)準(zhǔn)庫、解析器等等。我想到現(xiàn)在為止,它也應(yīng)該包含了機器學(xué)習(xí)庫(ML library)。
不管現(xiàn)實是怎么樣的,這個震撼的課程都值得我們?nèi)W(xué)習(xí)。人們現(xiàn)在把 TensorFlow 和類似的庫當(dāng)作理所當(dāng)然了。他們把它看作黑盒子并讓它運行起來,但是并沒有多少人知道在這背后的運行原理。這只是一個非凸(Non-convex)的優(yōu)化問題!請停止對代碼無意義的胡搞——僅僅只是為了讓代碼看上去像是正確的。
TensorFlow
在 TensorFlow 的代碼里,有一個重要的組件,允許你將計算串在一起,形成一個稱為「計算圖」的東西。這個計算圖是一個有向圖 G=(V,E),其中在某些節(jié)點處 u1,u2,…,un,v∈V,和 e1,e2,…,en∈E,ei=(ui,v)。我們知道,存在某種計算圖將 u1,…,un 映射到 vv。
舉個例子,如果我們有 x + y = z,那么 (x,z),(y,z)∈E。
這對于評估算術(shù)表達式非常有用,我們能夠在計算圖的匯點下找到結(jié)果。匯點是類似 v∈V,∄e=(v,u) 這樣的頂點。從另一方面來說,這些頂點從自身到其他頂點并沒有定向邊界。同樣的,輸入源是 v∈V,∄e=(u,v)。
對于我們來說,我們總是把值放在輸入源上,而值也將傳播到匯點上。
反向模式求微分
如果你覺得我的解釋不正確,可以參考下這些幻燈片的說明。
微分是 Tensorflow 中許多模型的核心需求,因為我們需要它來運行梯度下降。每一個從高中畢業(yè)的人都應(yīng)該知道微分的意思。如果是基于基礎(chǔ)函數(shù)組成的復(fù)雜函數(shù),則只需要求出函數(shù)的導(dǎo)數(shù),然后應(yīng)用鏈?zhǔn)椒▌t。
超級簡潔的概述
如果我們有一個像這樣的函數(shù):
對 x 求導(dǎo):
對 y 求導(dǎo):
其它的例子:
其導(dǎo)數(shù)是:
所以其梯度是:
鏈?zhǔn)椒▌t,例如應(yīng)用于 f(g(h(x))):
在 5 分鐘內(nèi)倒轉(zhuǎn)模式
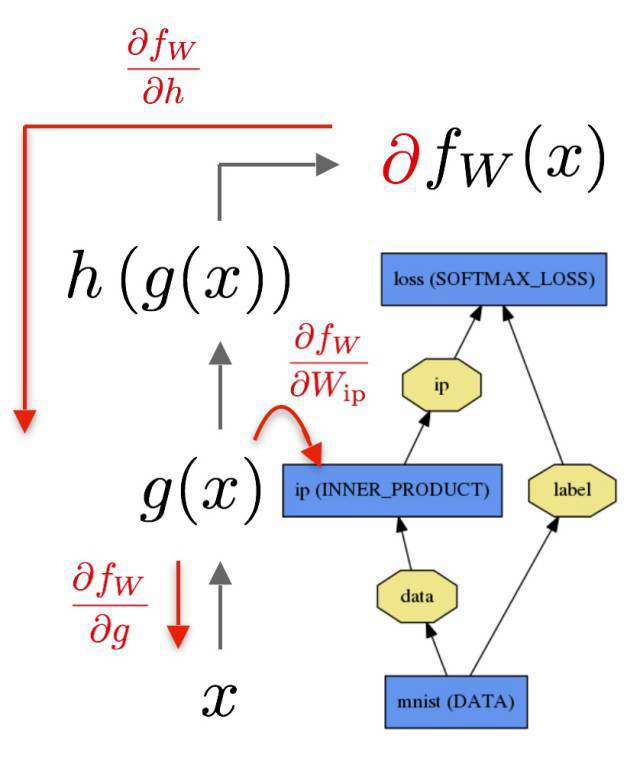
所以現(xiàn)在請記住我們運行計算圖時用的是有向無環(huán)結(jié)構(gòu)(DAG/Directed Acyclic Graph),還有上一個例子用到的鏈?zhǔn)椒▌t。正如下方所示的形式:
- x -> h -> g -> f
作為一個圖,我們能夠在 f 獲得答案,然而,也可以反過來:
- dx <- dh <- dg <- df
這樣它看起來就像鏈?zhǔn)椒▌t了!我們需要沿著路徑把導(dǎo)數(shù)相乘以得到最終的結(jié)果。這是一個計算圖的例子:
這就將其簡化為一個圖的遍歷問題。有誰察覺到了這就是拓撲排序和深度優(yōu)先搜索/寬度優(yōu)先搜索?
沒錯,為了在兩種路徑都支持拓撲排序,我們需要包含一套父組一套子組,而匯點是另一個方向的來源。反之亦然。
執(zhí)行
在開學(xué)前,Minh Le 和我開始設(shè)計這個項目。我們決定使用特征庫后端(Eigen library backend)進行線性代數(shù)運算,這個庫有一個叫做 MatrixXd 的矩陣類,用在我們的項目中:
- class var {// Forward declarationstruct impl;public:
- // For initialization of new vars by ptr var(std::shared_ptr<impl>);
- var(double);
- var(const MatrixXd&);
- var(op_type, const std::vector<var>&);
- ...
- // Access/Modify the current node value MatrixXd getValue() const;
- void setValue(const MatrixXd&);
- op_type getOp() const;
- void setOp(op_type);
- // Access internals (no modify) std::vector<var>& getChildren() const;
- std::vector<var> getParents() const;
- ...private:
- // PImpl idiom requires forward declaration of the class: std::shared_ptr<impl> pimpl;};struct var::impl{public:
- impl(const MatrixXd&);
- impl(op_type, const std::vector<var>&);
- MatrixXd val;
- op_type op;
- std::vector<var> children;
- std::vector<std::weak_ptr<impl>> parents;};
在這里,我們使用了一個叫「pImpl」的語法,意思是「執(zhí)行的指針」。它有很多用途,比如接口的解耦實現(xiàn),以及當(dāng)在堆棧上有一個本地接口時實例化內(nèi)存堆上的東西。「pImpl」的一些副作用是微弱的減慢運行時間,但是編譯時間縮短了很多。這允許我們通過多個函數(shù)調(diào)用/返回來保持數(shù)據(jù)結(jié)構(gòu)的持久性。像這樣的樹形數(shù)據(jù)結(jié)構(gòu)應(yīng)該是持久的。
我們有一些枚舉來告訴我們目前正在進行哪些操作:
- enum class op_type {
- plus,
- minus,
- multiply,
- divide,
- exponent,
- log,
- polynomial,
- dot,
- ...
- none // no operators. leaf.};
執(zhí)行此樹的評估的實際類稱為 expression:
- class expression {public:
- expression(var);
- ...
- // Recursively evaluates the tree. double propagate();
- ...
- // Computes the derivative for the entire graph. // Performs a top-down evaluation of the tree. void backpropagate(std::unordered_map<var, double>& leaves);
- ... private:
- var root;};
在反向傳播里,我們的代碼能做類似以下所示的事情:
- backpropagate(node, dprev):
- derivative = differentiate(node)*dprev
- for child in node.children:
- backpropagate(child, derivative)
這幾乎就是在做一個深度優(yōu)先搜索(DFS),你發(fā)現(xiàn)了嗎?
為什么是 C++?
在實際過程中,C++可能并不適合做這類事情。我們可以在像「Oaml」這樣的函數(shù)式語言中花費更少的時間開發(fā)。現(xiàn)在我明白為什么「Scala」被用于機器學(xué)習(xí)中,主要就是因為「Spark」。然而,使用 C++有很多好處。
Eigen(庫名)
舉例來說,我們可以直接使用一個叫「Eigen」的 TensorFlow 的線性代數(shù)庫。這是一個不假思索就被人用爛了的線性代數(shù)庫。有一種類似于我們的表達式樹的味道,我們構(gòu)建表達式,它只會在我們真正需要的時候進行評估。然而,使用「Eigen」在編譯的時間內(nèi)就能決定什么時候使用模版,這意味著運行的時間減少了。我對寫出「Eigen」的人抱有很大的敬意,因為查看模版的錯誤幾乎讓我眼瞎!
他們的代碼看起來類似這樣的:
- Matrix A(...), B(...);
- auto lazy_multiply = A.dot(B);
- typeid(lazy_multiply).name(); // the class name is something like Dot_Matrix_Matrix.
- Matrix(lazy_multiply); // functional-style casting forces evaluation of this matrix.
這個特征庫非常的強大,這就是它作為 TensortFlow 主要后端之一的原因,即除了這個慵懶的評估技術(shù)之外還有其它的優(yōu)化。
運算符重載
在 Java 中開發(fā)這個庫很不錯——因為沒有 shared_ptrs、unique_ptrs、weak_ptrs;我們得到了一個真實的,有用的圖形計算器(GC=Graphing Calculator)。這大大節(jié)省了開發(fā)時間,更不必說更快的執(zhí)行速度。然而,Java 不允許操作符重載,因此它們不能這樣:
- // These 3 lines code up an entire neural network!
- var sigm1 = 1 / (1 + exp(-1 * dot(X, w1)));
- var sigm2 = 1 / (1 + exp(-1 * dot(sigm1, w2)));
- var loss = sum(-1 * (y * log(sigm2) + (1-y) * log(1-sigm2)));
順便說一下,上面是實際使用的代碼。是不是非常的漂亮?我想說的是這甚至比 TensorFlow 里的 Python 封裝還更優(yōu)美!我只是想表明,它們也是矩陣。
在 Java 中,有一連串的 add(), divide() 等等是非常難看的。更重要的是,這將讓用戶更多的關(guān)注在「PEMDAS」上,而 C++的操作符則有非常好的表現(xiàn)。
特征,而不是一連串的故障
在這個庫中,可以確定的是,TensorFlow 沒有定義清晰的 API,或者有但我不知道。例如,如果我們只想訓(xùn)練一個特定子集的權(quán)重,我們可以只對我們感興趣的特定來源做反向傳播。這對于卷積神經(jīng)網(wǎng)絡(luò)的遷移學(xué)習(xí)非常有用,因為很多時候,像 VGG19 這樣的大型網(wǎng)絡(luò)可以被截斷,然后附加一些額外的層,這些層的權(quán)重使用新領(lǐng)域的樣本來訓(xùn)練。
基準(zhǔn)
在 Python 的 TensorFlow 庫中,對虹膜數(shù)據(jù)集進行 10000 個「Epochs」的訓(xùn)練以進行分類,并使用相同的超參數(shù),我們有:
- TensorFlow 的神經(jīng)網(wǎng)絡(luò): 23812.5 ms
- 「Scikit」的神經(jīng)網(wǎng)絡(luò):22412.2 ms
- 「Autodiff」的神經(jīng)網(wǎng)絡(luò),迭代,優(yōu)化:25397.2 ms
- 「Autodiff」的神經(jīng)網(wǎng)絡(luò),迭代,無優(yōu)化:29052.4 ms
- 「Autodiff」的神經(jīng)網(wǎng)絡(luò),帶有遞歸,無優(yōu)化:28121.5 ms
令人驚訝的是,Scikit 是所有這些中最快的。這可能是因為我們沒有做龐大的矩陣乘法。也可能是 TensorFlow 需要額外的編譯步驟,如變量初始化等等。或者,也許我們不得不在 python 中運行循環(huán),而不是在 C 中(Python 循環(huán)真的非常糟糕!)我自己也不是很確定。我完全明白這絕不是一種全面的基準(zhǔn)測試,因為它只在特定的情況下應(yīng)用了單個數(shù)據(jù)點。然而,這個庫的表現(xiàn)并不能代表當(dāng)前***,所以希望各位讀者和我們共同完善。