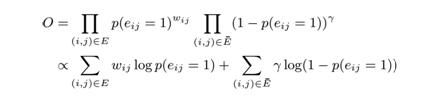如何實現大規模高維數據的可視化?
原創【51CTO.com原創稿件】數據可視化是脫胎于計算機圖形學的計算機學科領域,廣泛應用于科學實驗和互聯網商業應用。它分為科學可視化和信息可視化兩個子領域。
科學可視化主要是針對化學、物理和醫學上的試驗數據,將實驗結果用美觀可讀的方式展現給科學工作者,方便其進行后續的工作,美國的國家實驗室比如 LLNL 都有專門的團隊開展可視化方面的工作。
信息可視化更多的是針對互聯網和商業數據,主要是把數據用更清晰和直觀的方式傳遞給用戶,美國的紐約時報是這方面做得非常好的公司。
整個可視化領域的頂級會議是 IEEE Visualization。信息可視化領域的頂級會議是 IEEE InfoVis。可視化領域的頂級期刊是 IEEE TVCG (IEEE Transactions on Visualization and Computer Graphics)。美國猶他大學(University of Utah)的 SCI Institute 是全世界在可視化研究領域做得最好的研究機構之一,在國際上享有盛名。
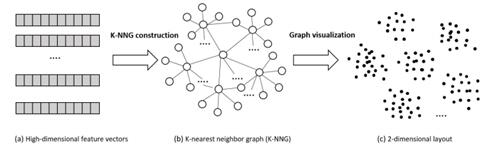
高維數據的可視化是可視化領域中非常具有挑戰性的一類問題。常見的解決方案包括 Parallel Coordinate,Star Plot,降維至低維空間進行可視化等。Jian Tang 等在 WWW 2016 上發表了題為 Visualizing Large-Scale and High-Dimensional Data 的文章,講述了他們是如何解決大規模高維數據的可視化問題的。下面我們來看一下他們提出的方法,分為兩步:
第一步將高維空間的數據利用K-近鄰算法重新構建社交網絡模型,第二步將新構建的社交網絡模型映射到低維空間進行可視化,參見下圖:
作者在執行第一步時,采取了類似 t-SNE 算法中的方式,而在執行第二步時采取了優化最大似然函數的方式。
首先,定義高維空間中映射到低維空間的兩個點的坐標是![]() 定義在低維空間中兩個點之間存在一條邊的概率是:
定義在低維空間中兩個點之間存在一條邊的概率是:![]() f 函數可以按照如下方式進行定義:
f 函數可以按照如下方式進行定義:![]() 帶權邊的生成概率為
帶權邊的生成概率為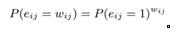 整個低維空間的社交網絡生成概率為:
整個低維空間的社交網絡生成概率為:
通過對 O 的求解,我們可以得到高維空間數據在低維空間的映射。注意在生成概率公式中存在對于負邊概率的大量計算。因為負邊的數量與節點的數量是成二次方關系的,因此作者對于負邊采取了負采樣的策略。也就是給定點i,隨機選取節點 j 與之構成負邊。選擇 j 的概率為![]()
為了避免在梯度下降過程中難以選擇學習率的問題,作者采用了在其本人的其他文獻中提出的 Edge Sampling 優化方法對似然函數進行優化。Edge Sampling 優化方法將圖的每一條邊看作沒有權重的邊,在進行梯度下降優化的時候根據邊的權重對每一條邊進行采樣。
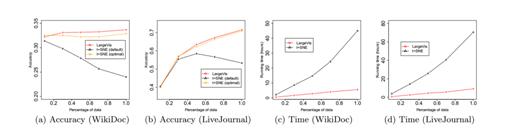
后續,作者選取了文本數據,并且利用了 KNN 分類器對降維處理之后的數據進行分類,從準確性和時間兩方面對 t-SNE 和作者提出的算法進行了對比,發現作者提出的方法要優于經典的 t-SNE 算法。
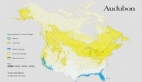
下圖為英文 Wikipedia 文章的可視化。每篇文章被認為是高維空間中的一個點。作者在 Wikipedia 數據集上進行了聚類,并對不同的類染上了不同的顏色。

圖2. 英文 Wikipeida 文章可視化。不同的顏色代表不同的文章分類。
Jian Tang , Jingzhou Liu , Ming Zhang , Qiaozhu Mei , Visualizing Large-scale and High Dimensional Data
汪昊,恒昌利通大數據部負責人,美國猶他大學碩士,在百度,新浪,網易,豆瓣等公司有多年的研發和技術管理經驗,擅長機器學習,大數據,推薦系統,社交網絡分析,計算機圖形學,可視化等技術。在 TVCG 和 ASONAM 等國際會議和期刊發表論文 5 篇。本科畢業論文獲國際會議 IEEE SMI 2008 最佳論文獎。
【51CTO原創稿件,合作站點轉載請注明原文作者和出處為51CTO.com】