從原理到應用:簡述Logistic回歸算法
Logistic 回歸是二分類任務中最常用的機器學習算法之一。它的設計思路簡單,易于實現,可以用作性能基準,且在很多任務中都表現很好。
因此,每個接觸機器學習的人都應該熟悉其原理。Logistic 回歸的基礎原理在神經網絡中也可以用到。在這篇文章中,你將明白什么是 Logistic 回歸、它是如何工作的、有哪些優缺點等等。
什么是 Logistic 回歸?
和很多其他機器學習算法一樣,邏輯回歸也是從統計學中借鑒來的,盡管名字里有回歸倆字兒,但它不是一個需要預測連續結果的回歸算法。
與之相反,Logistic 回歸是二分類任務的首選方法。它輸出一個 0 到 1 之間的離散二值結果。簡單來說,它的結果不是 1 就是 0。
癌癥檢測算法可看做是 Logistic 回歸問題的一個簡單例子,這種算法輸入病理圖片并且應該辨別患者是患有癌癥(1)或沒有癌癥(0)。
它是如何工作的?
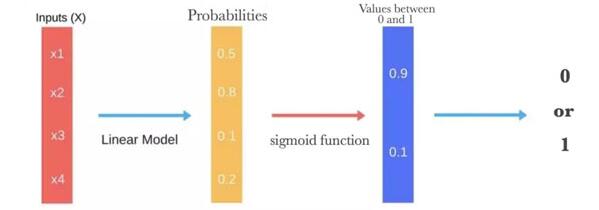
Logistic 回歸通過使用其固有的 logistic 函數估計概率,來衡量因變量(我們想要預測的標簽)與一個或多個自變量(特征)之間的關系。
然后這些概率必須二值化才能真地進行預測。這就是 logistic 函數的任務,也稱為 sigmoid 函數。Sigmoid 函數是一個 S 形曲線,它可以將任意實數值映射到介于 0 和 1 之間的值,但并不會取到 0/1。然后使用閾值分類器將 0 和 1 之間的值轉換為 0 或 1。
下面的圖片說明了 logistic 回歸得出預測所需的所有步驟。
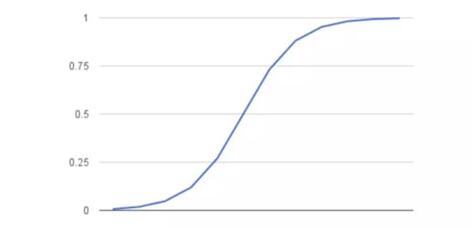
下面是 logistic 函數(sigmoid 函數)的圖形表示:
我們希望隨機數據點被正確分類的概率最大化,這就是最大似然估計。最大似然估計是統計模型中估計參數的通用方法。
你可以使用不同的方法(如優化算法)來最大化概率。牛頓法也是其中一種,可用于查找許多不同函數的最大值(或最小值),包括似然函數。也可以用梯度下降法代替牛頓法。
Logistic 回歸 vs 線性回歸
你可能會好奇:logistic 回歸和線性回歸之間的區別是什么。邏輯回歸得到一個離散的結果,但線性回歸得到一個連續的結果。預測房價的模型算是返回連續結果的一個好例子。該值根據房子大小或位置等參數的變化而變化。離散的結果總是一件事(你有癌癥)或另一個(你沒有癌癥)。
優缺點
Logistic 回歸是一種被人們廣泛使用的算法,因為它非常高效,不需要太大的計算量,又通俗易懂,不需要縮放輸入特征,不需要任何調整,且很容易調整,并且輸出校準好的預測概率。
與線性回歸一樣,當你去掉與輸出變量無關的屬性以及相似度高的屬性時,logistic 回歸效果確實會更好。因此特征處理在 Logistic 和線性回歸的性能方面起著重要的作用。
Logistic 回歸的另一個優點是它非常容易實現,且訓練起來很高效。在研究中,我通常以 Logistic 回歸模型作為基準,再嘗試使用更復雜的算法。
由于其簡單且可快速實現的原因,Logistic 回歸也是一個很好的基準,你可以用它來衡量其他更復雜的算法的性能。
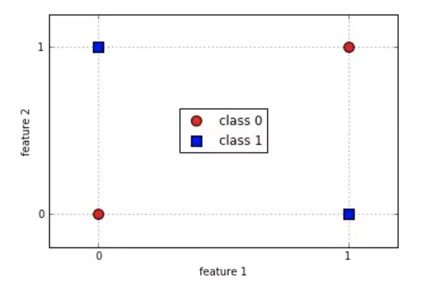
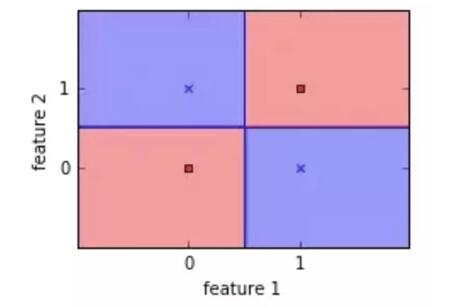
它的一個缺點就是我們不能用 logistic 回歸來解決非線性問題,因為它的決策面是線性的。我們來看看下面的例子,兩個類各有倆實例。
顯然,我們不可能在不出錯的情況下劃出一條直線來區分這兩個類。使用簡單的決策樹是個更好的選擇。
Logistic 回歸并非最強大的算法之一,它可以很容易地被更為復雜的算法所超越。另一個缺點是它高度依賴正確的數據表示。
這意味著邏輯回歸在你已經確定了所有重要的自變量之前還不會成為一個有用的工具。由于其結果是離散的,Logistic 回歸只能預測分類結果。它同時也以其容易過擬合而聞名。
何時適用
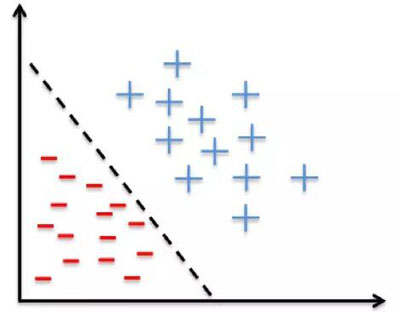
就像我已經提到的那樣,Logistic 回歸通過線性邊界將你的輸入分成兩個「區域」,每個類別劃分一個區域。因此,你的數據應當是線性可分的,如下圖所示的數據點:
換句話說:當 Y 變量只有兩個值時(例如,當你面臨分類問題時),您應該考慮使用邏輯回歸。注意,你也可以將 Logistic 回歸用于多類別分類,下一節中將會討論。
多分類任務
現在有很多多分類算法,如隨機森林分類器或樸素貝葉斯分類器。有些算法雖然看起來不能用于多分類,如 Logistic 回歸,但通過一些技巧,也可以用于多分類任務。
我們從包含手寫體 0 到 9 的數字圖像的 MNIST 數據集入手,討論這些最常見的「技巧」。這是一個多分類任務,我們的算法應該告訴我們圖像對應哪個數字。
1. 一對多(OVA)
按照這個策略,你可以訓練 10 個二分類器,每個數字一個。這意味著訓練一個分類器來檢測 0,一個檢測 1,一個檢測 2,以此類推。當你想要對圖像進行分類時,只需看看哪個分類器的預測分數最高
2. 一對一(OVO)
按照這個策略,要為每一對數字訓練一個二分類器。這意味著要訓練一個可以區分 0s 和 1s 的分類器,一個可以區分 0s 和 2s 的分類器,一個可以區分 1s 和 2s 的分類器,等等。如果有 N 個類別,則需要訓練 N×N(N-1)/ 2 個分類器,對于 MNIST 數據集,需要 45 個分類器。
當你要分類圖像時,就分別運行這 45 個分類器,并選擇性能最好的分類器。這個策略與其他策略相比有一個很大的優勢,就是你只需要在它要分類的兩個類別的訓練集上進行訓練。
像支持向量機分類器這樣的算法在大型數據集上擴展性不好,所以在這種情況下使用 Logistic 回歸這樣的二分類算法的 OvO 策略會更好,因為在小數據集上訓練大量分類器比在大數據集上訓練一個分類器要快。
在大多數算法中,sklearn 可以識別何時使用二分類器進行多分類任務,并自動使用 OvA 策略。特殊情況:當你嘗試使用支持向量機分類器時,它會自動運行 OvO 策略。
其它分類算法
其他常見的分類算法有樸素貝葉斯、決策樹、隨機森林、支持向量機、k-近鄰等等。我們將在其他文章中討論它們,但別被這些機器學習算法的數量嚇到。請注意,最好能夠真正了解 4 或 5 種算法,并將精力集中在特征處理上,這也是未來工作的主題。
總結
在這篇文章中,你已了解什么是 Logistic 回歸,以及它是如何工作的。你現在對其優缺點也了有深刻的了解,并且知道何時用它。
此外,你還探索了使用 Logistic 回歸與 sklearn 進行多分類的方法,以及為什么前者是比其他機器學習算法更好的基準算法。
原文鏈接:https://towardsdatascience.com/the-logistic-regression-algorithm-75fe48e21cfa
【本文是51CTO專欄機構“機器之心”的原創譯文,微信公眾號“機器之心( id: almosthuman2014)”】