區塊鏈科普:非對稱加密、橢圓曲線加密算法
區塊鏈加密介紹
區塊鏈加密技術
區塊鏈技術的應用和開發,數字加密技術是關鍵。一旦加密方法遭到破解,區塊鏈的數據安全將受到挑戰,區塊鏈的不可篡改性將不復存在。
加密算法一般分為對稱加密和非對稱加密,區塊鏈中主要應用非對稱加密算法。非對稱加密指為滿足安全性需求和所有權驗證需求而集成到區塊鏈中的加密技術。非對稱加密通常在加密和解密過程中使用兩個非對稱的密碼,分別稱為公鑰和私鑰。非對稱密鑰對具有兩個特點:一是用其中一個密鑰(公鑰或私鑰)加密信息后,只有另一個對應的密鑰才能解開。二是公鑰可向其他人公開,私鑰則保密,其他人無法通過該公鑰推算出相應的私鑰。
非對稱加密應用場景
非對稱加密技術在區塊鏈的應用場景主要包括信息加密、數字簽名和登錄認證等,其中信息加密場景主要是由信息發送者(記為A)使用接受者(記為B)的公鑰對信息加密后再發送給B,B利用自己的私鑰對信息解密。比特幣交易的加密即屬于此場景。數字簽名場景則是由發送者A 采用自己的私鑰加密信息后發送給B,B使用A 的公鑰對信息解密、從而可確保信息是由A發送的。登錄認證場景則是由客戶端使用私鑰加密登錄信息后發送給服務器,后者接收后采用該客戶端的公鑰解密并認證登錄信息。
非對稱加密科普
密鑰配送問題
我們在平時生活中對我們的賬號、文件進行加密的時候,通常都用的都是對稱密碼。所謂對稱密碼就是加密和解密用的是同一個密碼。比如我們在注冊自己的微信賬號時,會輸入一個密碼防止別人來登錄。以后如果因為你手動退出,或者換了臺手機需要再次登錄微信的時候,只要再把這個密碼輸一遍就可以了。
對稱密碼在大多數情況下使用起來都沒有問題。但是在一些特定場合,就不那么好用了。舉個例子,如果小明想通過電子郵件給小紅寫一份情書,作為一個害羞而謹慎的人,他不想讓任何其他人偷看到,于是他在這封郵件中設置了一個密碼,收件人只有輸入了這個密碼才能看到郵件的內容。假設小紅的爸爸有經常檢查(tou kan)小紅郵件的習慣,但如果他不知道密碼,也就只能作罷。或者小明有一個情敵小強,他是個計算機高手,能夠利用黑客手段截獲小明和小紅之間發送的郵件,但是如果郵件加了密(并且密碼強度足夠的話),他也只能望洋興嘆了。
但問題來了,小明怎么才能把這個密碼告訴小紅呢。如果小明在和小紅見面的時候,直接當面告訴小紅密碼,并且約定以后兩個人的郵件往來都會用這個密碼加密,那自然是沒有問題。但是如果小明和小紅是異地戀呢。要是小明把密碼也通過一份郵件發給小紅,這個密碼就同樣有泄漏的可能,那加密郵件也就沒有任何意義了。當然通過電話、寄信、放鴿子等等方式傳遞密碼,在理論上都有可能被手段高明的小強截獲。所以這就是所謂的密鑰配送難題。
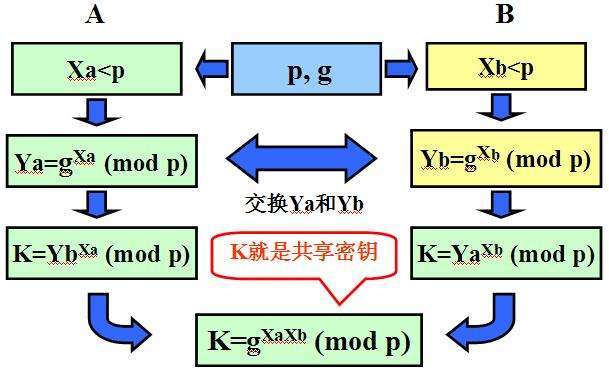
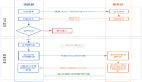
非對稱加密機制
針對密鑰配送這一難題,密碼學歷史上最偉大的發明——非對稱加密(公鑰加密)出現了。它解決了密鑰的發布和管理問題,是目前商業密碼的核心。在公鑰加密體制中,沒有公開的是私鑰,公開的是公鑰。
和對稱密碼不同,公鑰密碼體系由加密和解密兩組密鑰構成,他們之間是不同的。信息的發送者可以通過加密密鑰將信息進行加密,而接收者則會用解密密鑰來進行解密。
回到之前的那個例子,小紅同時擁有一對加密密鑰和解密密鑰。小紅把加密密鑰發送給小明,讓小明用這個密鑰把他想發的郵件進行加密后發給小紅自己。這個加密密鑰可以通過任何方式發送,郵件、電話、微信、信鴿都沒問題,甚至可以把它貼在家門口(當然,也沒必要這么張揚)。之所以膽子這么大,是因為這封被加密的郵件只有小紅通過自己手里掌握著的解密密鑰才能進行解密讀取。也就是說,即使小強通過黑客手段拿到了加密郵件,并且也知道了加密密鑰,只要他不知道解密密鑰,他還是沒有辦法讀到郵件。而這個關鍵的解密密鑰是被小紅自己保管的,它不會也不需要被發送給任何其他人,甚至包括小明。
由于加密密鑰通常是可以被公開的,所以它又被稱為公鑰;而解密密鑰是不能公開的,只能由自己來使用,所以又被稱為私鑰。公鑰和私鑰是永遠是成雙成對的,它們是不能分開生成的。
RSA算法
知道公鑰密碼的大致概念后,再來對它的實現方法作一下說明,好讓我們有一個更加直觀的認識。公鑰密碼有很多不同的實現方法,其中RSA算法是最為知名的一種,也可以說是現在公鑰密碼的事實標準,
RSA中的明文和密鑰都是數字。首先,RSA的加密公式為:
- 密文=明文^a % b
密文是將明文的a次方對b求余數的結果。任何人只要知道了a和b兩個數字,就可以通過這個公式把明文進行加密。換句話說,a和b共同構成了RSA加密算法的公鑰。
而RSA的解密公式
- 明文=密文^c % b
這個公式與之前唯一不同的就是把a換成了另一個數字c,而c和b則共同構成了RSA的私鑰。
把數字代進去舉個更加具體的例子,
比如,小明有一個明文數字123,想要把它加密后傳送給小紅。同時小紅手頭有一組密鑰對,其中公鑰是(a=5,b=323),私鑰是(c=29,b=323)。于是小紅把公鑰發給了小明。小明通過公鑰來對明文123進行加密計算后,得到了密文數字225,并把它發給了小紅:
- 密文=123^5 % 323=225
小紅拿到密文之后,用自己手中的私鑰進行了解密:
- 明文=225^29 % 323=123
這樣小紅就得到了原來的明文數字123,這里有很多細節被省去了,比如其中公鑰和私鑰中的數字5,29,323不是隨便取的,而是由特定算法生成的。
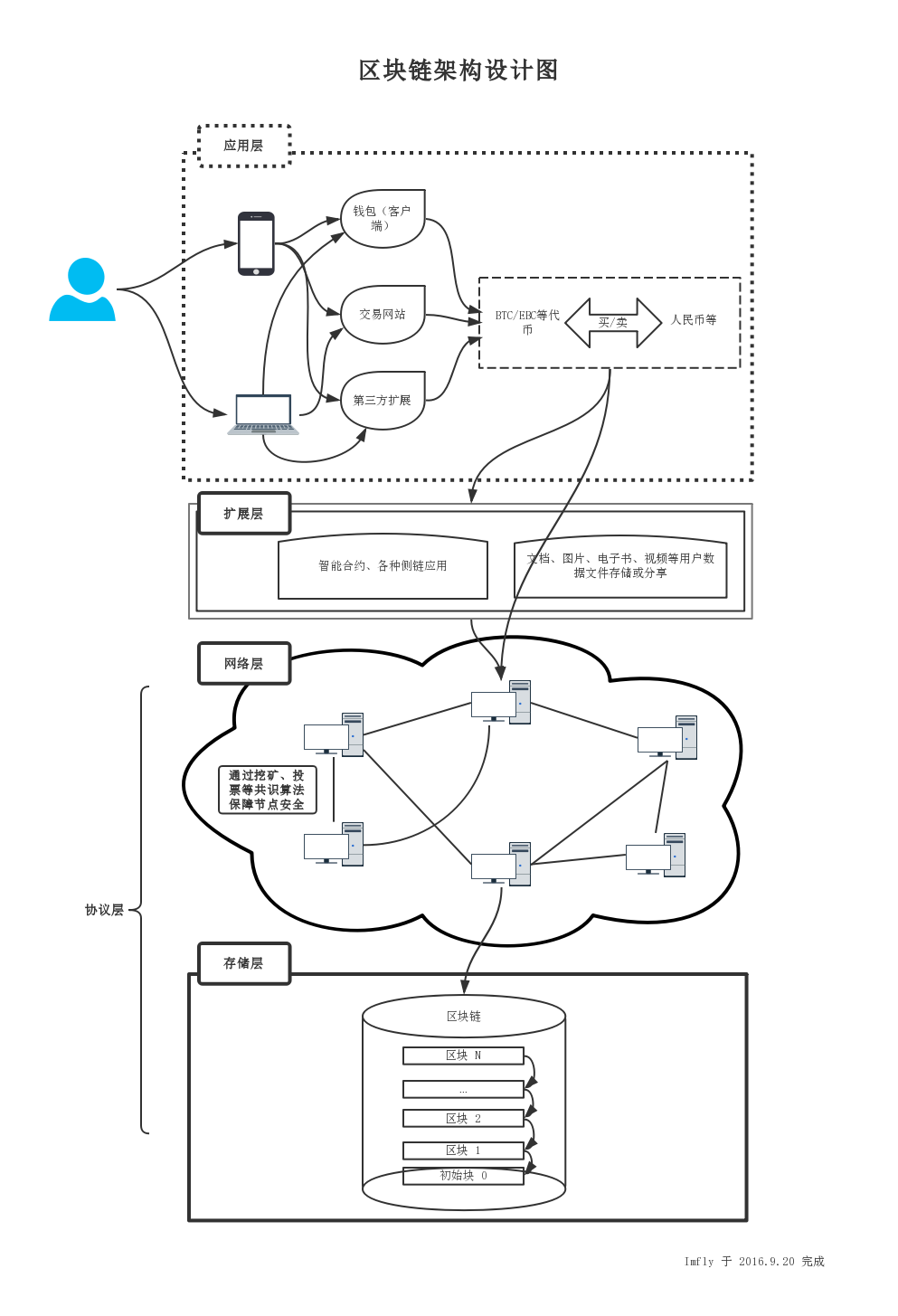
區塊鏈加密算法
加密簡單而言就是通過一種算法手段將對原始信息進行轉換,信息的接收者能夠通過秘鑰對密文進行解密從而得到原文的過程。按照加密方和解密方秘鑰相同與否可以將加密算法大致分為三種子類型:
- 對稱加密,加密解密方使用相同的秘鑰,這種方式的好處在于加解密的速度快但是秘鑰的安全分發比較困難,常見對稱加密算法有DES,AES。
- 非對稱加密,加解密時加密方擁有公鑰和私鑰,加密方可以將公鑰發送給其他相關方,私鑰嚴格自己保留。例如銀行的頒發給個人用戶的私鑰就存儲在個人的U盾里;非對稱加密中可以通過私鑰加密,他人能夠使用公鑰進行解密,反之亦然;非對稱加密算法一般比較復雜執行時間相對對稱加密較長;好處在于無秘鑰分發問題。常見的其他非對稱加密算法有RSA,ECC。
- 對稱加密與非對稱加密的結合,這種方式將加密過程分為兩個階段,階段一使用非對稱加密進行秘鑰的分發使得對方安全地得到對稱加密的秘鑰,階段二使用對稱加密對原文進行加解密。

區塊鏈中主要使用非對稱加密的ECC橢圓曲線算法。
橢圓曲線加密算法
橢圓曲線長什么樣
橢圓曲線如果用公式表示的話,可以寫成下面這樣:
- y^2 = x^3 + ax + b
其中,a和b取不同的值時,曲線的樣子也有所不同,比如說:
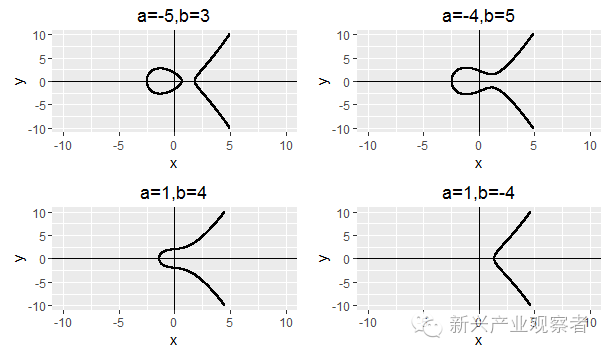
是不是感覺樣子有些怪,不管a和b取什么值,看上去都不像是橢圓形。據說橢圓曲線的名字來源于它的表達式有點像計算橢圓周長的積分公式,而不是說這個曲線畫出來是橢圓形~
橢圓曲線的加法和乘法
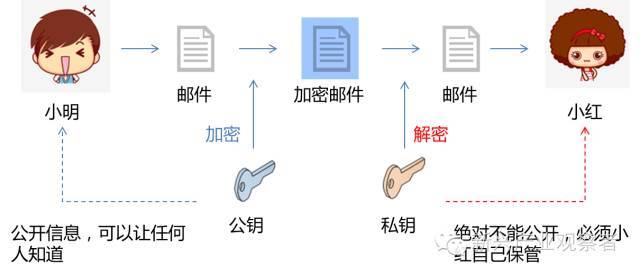
橢圓曲線的世界里,定義了一種奇怪的加法法則:任意取橢圓曲線上的兩點P、Q 畫一條直線,這條直線與曲線上的另個一交點為R',而R'關于x軸的鏡像點為R,那么P、Q、R這三個點相互之間就會形成這樣的關系:P+Q=R(其中R'=-R)。是不是有點特別,這個加法法則和我們平常理解的1+2=3是不同的,它建立了一種橢圓曲線上點和點之間的關系。
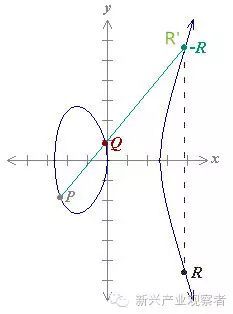
如果P和Q是同一個點,姑且都叫P吧,那么我們過P點畫一條橢圓曲線的切線,也可以得到一個它和曲線的另一個交點R',而R'同樣有一個相對于x軸的鏡像點R,這時候的加法就變成了P+P=2P=R,也就是變成了一個乘法運算。
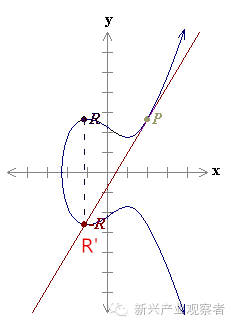
再延伸一步,如果以R為起點,還可以畫出一個新的點用來表示2R,也就是4P,然后再以這個新的點為起點還可以繼續畫下去……下面這個圖就是以G為起點,畫出了2G,4G,8G的樣子。
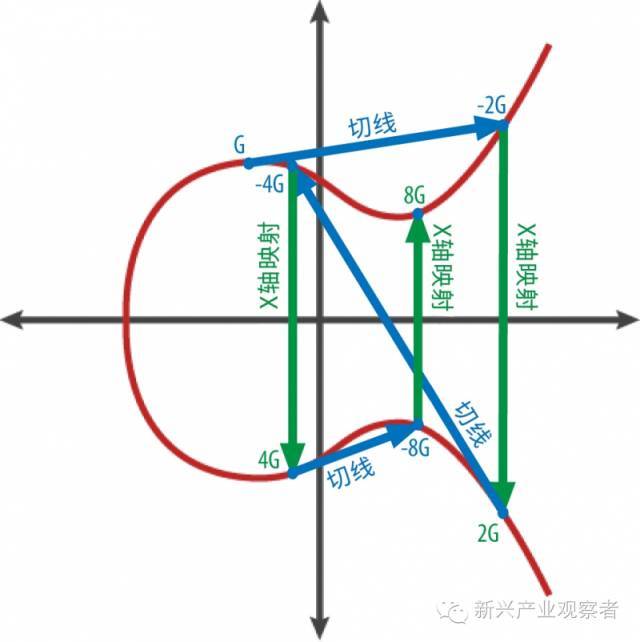
離散橢圓曲線
上面的講解中,我們看到橢圓曲線是條連續的曲線,之所以連續,是因為我們是在實數范圍內取值的,也就是說曲線上各個點的橫坐標和縱坐標都是實數。
可是,如果要把橢圓曲線應用于加密,是不能用實數的。因為實數包括了整數和小數,而小數不僅會讓計算速度大幅降低,計算結果還會涉及到四舍五入的問題,從而使計算精度受到影響。由于密碼學對于速度和精度都有嚴格的要求,所以我們是沒法用實數來對信息進行加密的。
為了讓橢圓曲線應用于加密,必須對其離散化,說白了也就是曲線上各個點的橫坐標和縱坐標都必須是整數,而且這些點的數量還得是有限的。讓我們舉個例子看看吧。
假設我們把橢圓曲線y^2= x^3 + x(a=1,b=0)離散化,并且規定只能取23個點,那么這23個點的橫坐標和縱坐標必須是0-22之間的整數,且橫縱坐標之間必須滿足下面這種關系(其中%表示取余數):
- y^2 % 23 = x^3 + x % 23
如果將這23個點畫出來,將會變成下圖的樣子。是不是感覺和連續的橢圓曲線有些不大一樣呢。
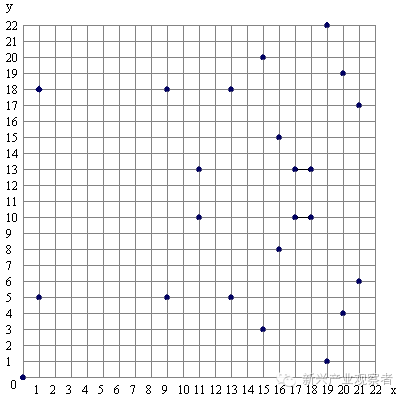
我們可以隨便取一個點(9,5)來看看是不是滿足上面的公式:
- 5^2 % 23 = 9^3 + 9 % 23
- 25 % 23 = 738 % 23
- 2=2
離散橢圓曲線上的加法和乘法也遵循類似于連續橢圓曲線的規則,不過因為都是一個個離散點,其運算過程也就沒有辦法像連續橢圓曲線中那樣形象地表示出來了。舉兩個例子感受一下吧,比如
- 加法:P(11,10)+Q(1,5)=R(17,10)
- 乘法:2P(11,10)=R(13,18)
(由于不是在上數學課,所以這里相應的計算公式也就不再列出了,我們不去深挖細節,只要知道大致原理就好)
也就是說,所有的23個點之間都有一種奇妙的聯系,任意兩個點相加,或者任意一個點的倍數得到的結果都會是這23個點中的另一個點。就好像這23個點之間形成了一套自己的封閉的數學體系。
應用于比特幣中的橢圓曲線
那么應用到區塊鏈中的橢圓曲線到底是個什么樣子呢?
事實上,不是所有的橢圓曲線都能夠保證足夠的安全性從而用于加密,而區塊鏈技術的最典型應用比特幣中所使用的橢圓曲線遵循了一種叫做secp256k1的標準,這個標準所定義的橢圓曲線方程是這個樣子的:
- y^2 % p = x^3 + 7 % p
其中p是一個非常非常大的素數:
- p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1
也就是說,這是一個由p個點構成的離散橢圓曲線。
使用橢圓曲線生成公鑰
說了一大堆橢圓曲線的基本原理,那么它到底是怎么應用到比特幣中去的呢?
其實,橢圓曲線在比特幣中扮演的角色說起來也很簡單,就是用來生成公鑰。
在上一篇文章中我們講到,公鑰加密體系的機制是一條信息可以通過公鑰來加密,并且通過私鑰來解密,而公私鑰必須是成對出現的。事實上,公鑰是由私鑰通過一定的算法計算出來的。而在比特幣中,公鑰是通過橢圓曲線算法由私鑰生成的。
具體來說,假設我們有一個私鑰k,只要將其與橢圓曲線上的一個初始點G相乘,就可以獲得曲線上的另一點,也就是相應的公鑰K。而這個乘法的計算方式用的就是我們之前所講到的運算法則。
K(公鑰) = k(私鑰) * G(橢圓曲線上的初始點)
事實上,初始點G作為secp256k1標準的一部分,是一個固定的點,相當于一個常數。所以,私鑰k和公鑰K之間的關系是固定的。不過,這個計算只能單向運算,即我們可以從私鑰k得到公鑰K,但反過來就做不到了,而這就是可以把公鑰與任何人共享而不會泄露私鑰的原因。下面舉個例子,讓我們看一下比特幣的公私鑰是什么樣子。
比特幣的私鑰是一個256位的二進制數字,通常用64位的16進制數顯示,就像下面這樣:
- k=1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
通過把k與橢圓曲線上的初始點G相乘,就會得到公鑰K(x,y),x和y分別是K的橫縱坐標,其中:
- x=F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
- y=07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB