應用處理的數據量在持續增長。數據的增長，對擴展存儲能力提出了挑戰。就此問題，每種數據庫管理系統都有其自身的權衡考慮。對于數據管理者而言，理解這些權衡因素非常關鍵，這有助于從多種方式中做出正確的選擇。

[[238427]]

從讀 / 寫工作負載平衡、一致性需求、延遲和訪問模式等方面看，應用是各異的。如果我們能對數據庫和存儲內部設施架構決策了然于胸，那么將有助于我們理解系統行為模式的原因所在，一旦在問題時能解決問題，并能根據工作負載調優數據庫。

一個系統不可能在所有方面上都是***的。確保無存儲開銷、提供***讀寫性能的數據結構只存在于理想情況下，在實踐中當然是不可能存在的。

本文詳細剖析了兩種被大多數現代數據庫使用的存儲系統設計方法，即針對讀優化的 B 樹1和針對寫優化的 LSM（日志結構合并，log-structured merge）樹 5，并分別給出了兩種方法的一些用例和權衡考慮。

一、B 樹

B 樹是一種廣為使用的讀優化索引數據結構，是二叉樹的一種泛化。它具有多種變體，并已用于多種數據庫（包括 MySQL InnoDB4 和 PostgreSQL 7）和文件系統（例如，HFS+8、ext4 中的 HTrees 9）。B 樹中的“B”表示“Bayer”，指的是數據結構的最初創立者 Rudolf Bayer，也可以說是 Bayer 彼時供職的波音公司（Boeing）。

二叉樹中，每個節點有兩個子節點（分別稱為左子節點和右子節點）。保存在左子樹和右子樹中的鍵（Key），其值分別小于和大于當前節點的鍵。為維持樹的深度最小，二叉樹必須是平衡的。在添加隨機順序的鍵到樹中時，最終很自然會導致樹的一邊比另一邊更深。

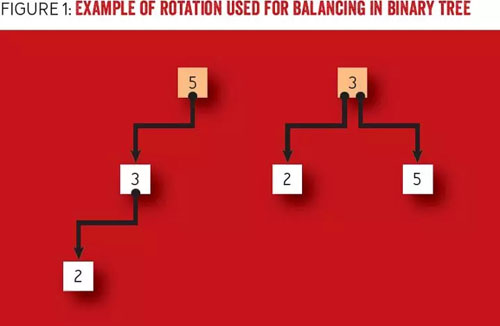
一種二叉樹重平衡（rebalance）的法是稱為“旋轉”（rotation）方法。旋轉方法實現節點的重新排列，它將更深子樹的父節點下推到其子節點之下，并上移子節點為有效地置于父節點的原位置。圖 1 給出了一個旋轉方法的例子，實現了一個二叉樹的平衡。左圖的二叉樹在添加了節點“2”之后，是不平衡的。為了平衡二叉樹，我們以節點“3”為軸心旋轉樹，然后以節點“5”為軸線。節點“5”是原先的根節點，也是節點“3”的父節點，旋轉后成為節點“3”的子節點。在完成旋轉后得到右圖的樹，其中左子樹深度降低了 1，右子樹的深度增加了 1，而樹的***深度降低了。

圖 1 例子：使用旋轉方法平衡二叉樹

二叉樹是一種十分有用的內存數據結構。由于平衡（即需要保持所有子樹的深度最小）和低扇出（每個節點最多具有兩個指針）特性，二叉樹在磁盤上的性能并不好。B 樹允許每個節點存儲兩個以上的指針，并可將節點大小調整為適合頁面的大小（例如，4KB），因此可在塊設備上良好工作。當前，有一些實現中使用了更大規模的節點，甚至橫跨多個頁面。

B 數據有如下屬性：

• 排序：排序支持順序掃描，簡化了查找。
• 自平衡：插入和刪除操作無需重平衡樹。一個 B 樹節點在占滿后，將分割（split）為兩個節點。如果兩個近鄰節點的利用率（occupancy）降至某個閾值以下時，那么節點會合并（merge）。這意味著，各個葉子節點與根節點間是等距的，在查找時可以使用同樣的步數定位。
• 查找操作有對數時間復雜度保證。這一點使 B 樹成為數據庫索引的很好選擇，因為在數據庫中，查找時間是非常關鍵的。
• 支持可變數據結構。插入、更新和刪除（以及隨后的節點分割和合并）是在磁盤上執行的，實現就地（in-depth）更新需要一定的空間開銷。B 樹可以組織為聚束索引，將實際數據存儲在葉子節點上，也可以使用非聚束索引，將數據存儲為堆文件。

本文還將介紹 B+ 樹 3。B+ 樹是 B 樹的一種變體，常用于數據庫存儲。與原始 B 樹相比，B+ 樹的不同之處在于：1. B+ 樹的葉子節點存儲值并形成一個額外的鏈接層。2.B+ 樹的內部節點并不存儲值。

B 樹剖析

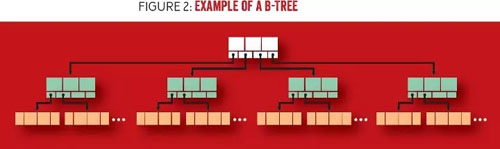
下面我們仔細查看 B 樹的構建模塊，如圖 2 所示。B 樹具有多種節點類型，包括根節點、內部節點和葉子節點。根節點（頂端）是沒有父節點的節點（即它不是任何其它節點的子節點）。內部節點（中間）具有父節點和子節點，它們連接了根節點和葉子節點。葉子節點（底端）保存數據，它沒有子節點。圖 2 顯示的 B 樹的分支因子（branching factor）為 4，即具有四個指針，內部節點有三個鍵值，葉子節點有四個鍵值對。

圖 2 例子：B 樹

標識一個 B 樹，可使用如下指標：

• 分支因子：即指向子節點的指針數（N）。考慮存在指針，根節點和內部節點***可保存 N-1 個鍵值。
• 利用率：***可用指針數中，當前有多少指向子項的指針在用。例如，如果樹的分支因子是 N，節點當前保持了 N/2 個指針，那么利用率就是 50%。
• 高度：B 樹的層數，指明了在查找中需遍歷的指針個數。

樹中每個非葉子節點最多保持 N 個鍵（索引項），將樹分割為 N+1 個子樹，這些子樹可用相應的指針定位。在條目 Ki 中的指針 i 指向的子樹中，所有索引項是 Ki-1 <= Ksearched < Ki（其中 k 是一組鍵）。***個和***一個指針是特例，最左子節點指向的子樹中，所有的條目小于或等于 K0；最右子節點指向的子樹中，所有的條目大于 KN-1。葉子節點中包含的指針，可指向同一層中前一個或后一個節點，形成近鄰節點的雙向鏈接列表。所有節點中，鍵總是排序的。

查找

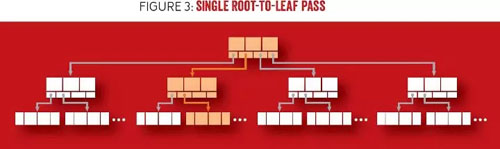
在執行查找時，搜索將從根節點開始，沿內部節點遞歸下行至葉子層級。在每一層級，通過追隨子節點指針，搜索空間可縮減到子樹范圍（該子樹包括搜索值）。圖 3 顯示的是 B 樹中的一次查找，即一次沿著兩個鍵間的指針由根到葉子的遍歷，一個指針大于或等于搜索項，另一個指針小于搜索項。執行一個點查詢（Point Query）時，搜索在定位到葉子節點后結束。在范圍搜索中，會遍歷所找到葉子節點的鍵和值，然后是近鄰的葉子節點，直到到達范圍的終點。

圖 3 單次由根到葉子的遍歷

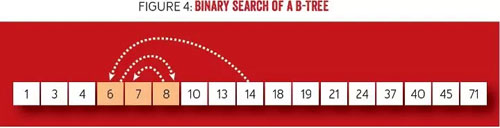
從復雜性上看，B 樹保證了 log(n) 復雜度的查找，因為如何從節點中找到鍵中使用了二分查找法，如圖 4 所示。二分查找法易于解釋，當從字典中搜索具有某個首字母的單詞時，所有單詞是按字母順序排列的。首先選擇從確切的中間位置打開字典。如果搜索字母在字母序上要“小于”（先出現）打開的字母，那么繼續在左半部份字典中搜索。否則，在詞典右半部份中搜索。然后繼續縮減剩余頁面范圍，通過減半并選擇搜索方向，直到找到所需的字母。每步將搜索空間減半，使查找呈對數時間復雜度。B 樹中的搜索具有對數時間復雜度，因為節點層級鍵是排序的，并在查找匹配總使用了二分查找。這也是為什么在整個樹中保持高利用率和一致性是非常重要的。

圖 4 B 樹的二分查找

插入、更新和刪除

執行插入時，***步是定位目標葉子節點。在此可使用上面介紹的搜索算法。定位目標節點后，鍵和值將添加到該節點中。如果葉子節點的空間不夠用，這種情況稱為“溢出”（Overflow），葉子節點必須分割為兩個。分割的實現是通過分配一個新葉子，將原葉子節點中的半數元素移動到新的葉子節點，并在父節點中分配一個指向新葉子節點的指針。如果父節點中也沒有空余的空間，那么就在父節點層級執行分割操作。操作將持續直至到達根節點。如果根節點溢出，節點內容在新分配節點間分割。然后根節點自身將被覆蓋，以避免重新分配。這也意味著，樹（及樹的高度）的高度總是在分割根節點時增長。

二、LSM 樹

日志結構合并（LSM）樹是一種寫優化的數據結構，它是不可變的、駐留于磁盤的，適用于寫操作比查找和檢索記錄更為頻繁的系統。由于 LSM 樹消除了隨機插入、更新和刪除，因此它得到了更多的關注。

LSM 樹剖析

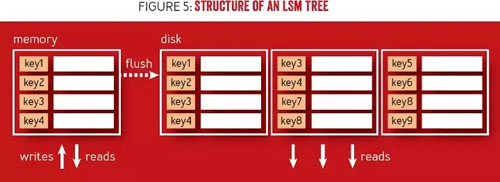
為支持順序寫，LSM 樹在一個駐留內存表（通常使用支持對數時間復雜度查找的數據結構實現，例如二分查找樹或跳表）中批量寫入和更新，直至內存表規模達到一個設定的閾值，這時再寫入到磁盤，該操作稱為“刷新”（flush）。檢索數據需要搜索樹駐留磁盤的所有部分，檢查駐留內存表，并在返回結果前合并內容。圖 5 顯示了一個 LSM 樹的結構，其中的駐留內存表用于寫入。一旦內存表達到了一定規模大，其中經排序的內容就要就寫入到磁盤。讀取時需要訪問駐留磁盤和駐留內存表，并需要一個合并過程去整合數據。

圖 5 LSM 樹的結構

排序字符串表（SSTable）

現代多種系統中，例如 RocksDB 和 Apache Cassandra，將 LSM 樹的駐留磁盤表實現為一種 SSTable（排序字符串表）。SSTable 具有簡單性（易于寫入、搜索和讀取）及合并屬性（在合并期間，源 SSTable 掃描和合并結果寫是順序操作）。

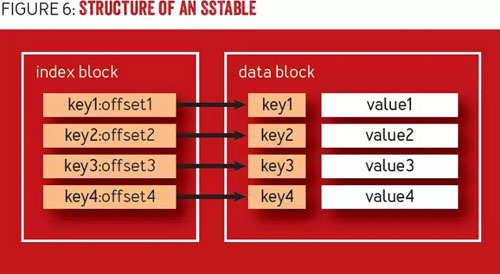
SSTable 是一種不可變的、駐留磁盤的排序數據結構。如圖 6 所示，SSTable 在結構上可分為兩個部分，即數據塊和索引塊。數據塊是由順序寫入的唯一鍵值對組成，鍵值對按鍵排序。索引塊中的鍵包含映射到數據塊指針，指針指向實際記錄的位置。索引通常實現為針對快速搜索優化的格式，例如 B 樹，或是對于點查詢使用哈希表。SSTable 中的每個值項具有一個與之相關聯的時間戳。時間戳指定了插入和更新的寫入時間（通常不做區分），以及刪除的移除時間。

圖 6 SSTable 的結構

SSTable 具有一些很好的特性：

• 點查詢（即根據鍵找到一個值）可通過查找主索引快速完成。
• 掃描（即在指定鍵范圍內迭代所有鍵值對）可以高效完成，僅通過在數據塊內順序讀取鍵值對。

SSTable 給出了一段時間內所有數據庫操作的快照。因為 SSTable 是由駐留內存表的刷新操作創建的，該表作為此時期內對數據庫狀態操作的一個緩沖區。

查找

檢索數據時，需要搜索磁盤上所有的 SSTable，檢查駐留內存表，并在返回結果前合并其中的內容。讀操作需要合并過程，因為所搜索的數據可能存在于多個 SSTable 中。

為確保實現刪除和更新，也必須要合并步驟。刪除時，會在 LSM 樹中插入一個占位符，通常稱為“墓碑”（tombstone）。墓碑用于標記被刪除的鍵。類似地，更新時也僅是增加一個具有更遲時間戳的記錄。在讀取期間，將跳過被標記為刪除的記錄，不返回給客戶。更新中也采取類似的做法，對于兩個具有同一鍵的記錄，只返回時間戳更晚的記錄。圖 7 顯示了合并是如何整合存儲在獨立表中具有同一鍵的數據。如圖所示，Alex 的記錄寫入的時間戳為 100，更新了電話后記錄的時間戳為 200。John 的記錄是被刪除的。其它兩個條目保持原狀，因為它們并未做標記。

圖 7 例子：合并步驟

為減少需搜索的 SSTable 數量，避免因為搜索某個鍵而檢查每個 SSTable，一些存儲系統使用了一種稱為布隆濾波器 10 的數據結構。布隆濾波器是一種概率數據結構，可用于檢測一個元素是否屬于一個集合的成員。它會產生誤報匹配（即指出元素是集合的成員，但是事實上并不是），但是不會產生漏報（即如果返回結果是不匹配，那么該元素一定不是集合的成員）。換句話說，布隆濾波器可用于告知一個鍵是否“可能位于 SSTable 中”，或是“絕對不在 SSTable 中”。如果一個 SSTable 被布隆濾波器返回為不匹配，那么將在查詢中跳過。

維護 LSM 樹

鑒于 SSTable 是不可變的、是順序寫的，并且并未保留就地更改的空間。這意味著，插入、更新和刪除操作需要重寫整個文件。所有修改數據庫狀態的操作，是在內存駐留表中“批量處理”的。隨時間的推進，駐留磁盤表的數量將會增長（對應同一鍵的數據可能會位于多個文件、同一記錄的多個版本，或標記為刪除的冗余記錄中），讀取將繼續變得代價更為昂貴。

為降低讀取的代價、整合被標記的記錄空間并降低駐留磁盤表的數量，LSM 樹需要一個緊縮（compaction）過程。緊縮過程從磁盤讀取整個 SSTable，并合并它們。因為 SSTable 是按鍵排序的，緊縮過程的工作方式類似于歸并排序，所以該操作也是非常高效。記錄從多個數據源順序讀取，合并的輸出可以即刻順序地附加到結果文件中。歸并排序的一個優點是工作高效，即便是對于歸并無法放入內存中的大型文件。生成的表將保持原始 SSTable 的排序。

在緊縮過程中，合并后的 SSTable 將被拋棄，并被更“緊縮”的表替代，如圖 8 所示。緊縮操作輸入為多個 SSTable，輸出為合并后的一個表。一些數據庫系統在邏輯上將同一規模的表分組為同一“層級”，并在某個層級中的表數量足夠多時，開始合并過程。緊縮減少了必須要處理的 SSTable 數量，使查詢更加高效。

圖 8 緊縮過程

原子性和持久性

為實現 I/O 操作數量減少和順序化，B 樹和 LSM 樹均在更新實際發生前做內存中的批處理。這意味著，一旦發生失敗，不能保證數據的完整性，而且也不能確保原子性（指一組更改的應用是原子化的，如同單個操作一樣，或者全部應用，或者全不應用）和持久性（確保在進程崩潰或掉電時，數據處于一致性存儲中）。

為解決這個問題，很多現代存儲系統使用了 WAL 技術（預寫式日志，Write-Ahead Logging）。WAL 的主要理念是所有數據庫狀態修改首先持久保持在位于磁盤上的只添加日志中。一旦操作過程中發生進程崩潰，就會重執行日志，以確保沒有數據丟失，實現所有更改的原子化。

B 樹中，使用 WAL 可理解為更改只有做日志后，才寫到數據文件中。通常情況下，B 樹存儲系統的日志規模相對較小。一旦更改應用到持久存儲，就會被丟棄。WAL 作為一種對未日志化（in-flight）操作的備份機制，即應用到數據頁面的任何更改都可以從日志記錄重做。

LSM 樹中，WAL 用于持久化那些操作了內存表但是并未完全刷新到磁盤的更改。一旦內存表完全刷新并切換，讀取操作可以在新創建的 SSTable 上完成，就可以丟棄保持了刷新內存表數據的 WAL 段。

總結

B 樹和 LSM 樹結構上的***差別之一，在于優化的目的，以及優化的意義。

下面對 B 樹和 LSM 樹做一個對比。總而言之，B 樹具有如下屬性：

• B 樹是可變的，這支持通過引入一些空間開銷，以及更為關聯的寫路徑，實現就地更新。B 樹并不需要完全的文件重寫或多源合并。
• B 樹是讀優化的。即 B 樹不需要從多個源讀取（因此也不需要此后的合并操作），這簡化了讀路徑。
• 寫可能會觸發節點的級聯分割，這會使一些寫操作更昂貴。
• B 樹是針對分頁（塊存儲）環境優化的，其中不存在字節地址。They are optimized for paged environments (block storage), where byte addressing is not possible.
• 雖然也需要重寫，但是通常情況下 B 樹存儲要比 LSM 樹存儲需要更少的維護。
• 并發訪問需要讀 / 寫隔離，其中一系列的鎖和閂（latch）。

LSM 樹具有如下特性：

• LSM 樹是不可寫的。SSTable 是一次性寫入磁盤的，永不更新。緊縮操作通過從多個數據文件移除條目，并合并具有相同鍵的數據，實現空間的整合。在緊縮過程中，已合并的 SSTable 將被丟棄，并在成功合并后移除。不可寫提供的另一個有用特性，就是刷新后的表可并發訪問。
• LSM 是寫優化的。這意味著寫入操作將被緩存，并順序地刷新到磁盤中，潛在地支持磁盤上的空間本地性。
• 讀操作可能需要從多個數據源訪問數據。因為不同時間寫入的具有相同鍵的數據，可能會落在不同的數據文件中。記錄在返回給客戶前，必須經過合并過程。
• LSM 樹需要做維護和緊縮，因為緩存的寫入操作將被刷新到磁盤。

三、存儲系統的評估

在存儲系統的開發中，總是需要考慮一些挑戰和因素。優化目標對存儲系統選擇有著切實的影響。如果可以在寫操作上花費更多時間，那么就可以部署針對更高效讀操作的結構，預留額外的空間用于就地更新。這有利于實現更快的寫操作，并支持將數據緩存在內存中，以確保順序的寫操作。但是，所有這些是不可能一次性達成的。我們理想中的存儲系統具有***的讀代價、***的寫代價，并沒有其它開銷。但在實踐中，數據結構需折衷考慮多個因素。理解這些折衷考慮是非常重要的。

哈佛大學 DASlab（數據系統實驗室）的研究人員總結了數據庫系統優化的三個關鍵參數：讀開銷、更新開銷和內存開銷，統稱為“RUM”。對于特定的用例，理解這些參數中哪個是最重要的，將對數據結構、訪問方法，甚至是特定工作負載的適用性產生影響，因為算法需要根據特定的用例做出調整。

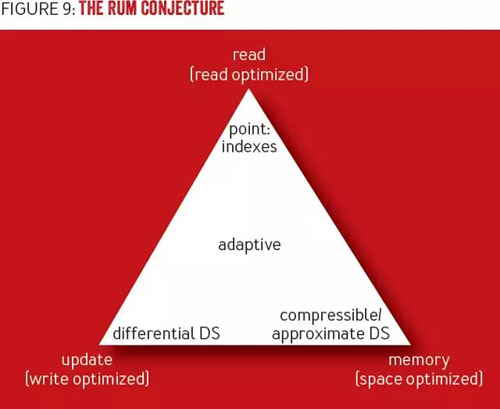
“RUM 假說”（http://daslab.seas.harvard.edu/rum-conjecture/）2 指出，如果對 RUM 中的兩項設置上限，那么也會對第三項設置下限。例如，B 樹是讀優化的，代價是寫開銷，以及預留了額外的空間（因而導致了內存開銷）。LSM 樹空間開銷更少，代價是在讀操作期間必須訪問多個駐留磁盤表，從而引入了讀開銷。這三個參數形成了一個完全三角形，改進其中的一項，意味著對其它項的折衷考慮。圖 9 展示了 RUM 假說。

圖 9 RUM 假說

B 樹是針對讀性能優化的。索引的布局方式使得遍歷樹所需的磁盤訪問次數最小化。定位數據時，只需訪問單個索引文件。這是通過保持索引文件可寫而實現的。可寫增加了寫入放大（Write Amplification）問題，該問題由節點分割、合并、重定位和碎片化 / 不平衡相關維護等導致。為緩解更新的代價，并降低分割的次數，B 樹在各個層級的節點中預留了額外的空閑空間。這有助于推遲發生寫入放大問題，直至節點空間滿。簡而言之，B 樹是在更新和內存開銷間做了權衡，目的是實現更好的讀性能。

LSM 樹針對寫性能優化。無論更新或是刪除，都需要定位數據在磁盤上的位置（B 樹也需要）。LSM 樹通過在內存駐留表緩存所有插入、更新和刪除操作以保證順序寫。這樣做的代價是更高的維護代價、需要緊縮操作（緊縮操作只是一種緩解不斷增長的讀代價、減少駐留磁盤表數量的方式），以及更昂貴的讀（因為數據必須從多個源讀取并合并）。同時，LSM 樹不保持任何空閑空間，這消除了一些內存開銷（不同于 B 樹節點平均利用率為 70%，就地更新需要一定的開銷）。由于 LSM 樹最終文件是不寫的，為實現更好的使用率，需要支持塊壓縮。簡而言之，LSM 樹是在讀性能和維護更好寫性能和低內存開銷間的權衡。

對于每種所需的特性，都會存在針對此特性優化的數據結構。如果使用相適應的數據結構以支持更好的讀性能，那么代價是更高的維護代價。添加元數據有利于遍歷（例如分散層疊（fractional cascading）），這將影響寫的時間，并占用空間，但是可以改進讀的時間。使用壓縮技術 (例如，Gorilla 壓縮 6、delta encoding 等算法) 可優化內存效率，將對寫時數據打包和讀時數據解包添加一些開銷。有時，我們可以權衡功能和效率。例如，堆文件和哈希索引由于文件格式的簡單性，可以給出很好的性能保證，以及更小的空間開銷，但代價是只能支持執行點查詢。我們還也可以通過使用近似數據結構，例如布隆濾波器、HyperLogLog、Count-Min sketch 等，權衡空間精度和效率。

讀、更新和內存這三種可調整的開銷，有助于我們評估數據庫，并更深入理解數據庫適合何種工作負載。三者非常直觀，很容易將存儲系統排序在一個桶中，給出執行情況的猜測，進而通過深入的測試去驗證這一假設。

當然，評估存儲系統時還存在其它一些重要的因素，例如維護代價、操作簡單性、系統需求、對頻繁更新和刪除的適用性、訪問模式等。RUM 假說僅是有助于給出直觀感覺，并對最初方向提供經驗法則。理解我們自己的工作負載，這是邁向構建可擴展的后端系統的***步。

在不同的實現中，一些因素可能會發生變化。即便是使用類似存儲設計原則的兩個數據庫間，最終的表現也可能會完全不同。數據庫是一個復雜的系統，其中有很多變動因素。數據庫也是很多應用中重要且不可分割的部分。性能上的權衡有助于我們一窺數據庫的底層機制。了解底層數據結構及內部原理間的差異，有助于我們從中做出***的選擇。

參考文獻

Comer, D. 1979. The ubiquitous B-tree. Computing Surveys 11(2); 121-137;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.96.6637.

哈佛大學 DASlab 實驗室. The RUM Conjecture;

http://daslab.seas.harvard.edu/rum-conjecture/.

Graefe, G. 2011. Modern B-tree techniques. Foundations and Trends in Databases 3(4): 203-402;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.219.7269&rep=rep1&type=pdf.

MySQL 5.7 參考手冊. InnoDB 索引的物理結構 ;

https://dev.mysql.com/doc/refman/5.7/en/innodb-physical-structure.html.

O'Neil, P., Cheng, E., Gawlick, D., O'Neil, E. 1996. The log-structured merge-tree. Acta Informatica 33(4): 351-385;

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.44.2782.

Pelkonen, T., Franklin, S., Teller, J., Cavallaro, P., Huang, Q., Meza, J., Veeraraghavan, K. 2015. Gorilla: a fast, scalable, in-memory time series database. Proceedings of the VLDB Endowment 8(12): 1816-1827;

http://www.vldb.org/pvldb/vol8/p1816-teller.pdf.

Suzuki, H. 2015-2018. The internals of PostgreSQL;

http://www.interdb.jp/pg/pgsql01.html.

Apple HFS Plus Volume 格式 ;

https://developer.apple.com/legacy/library/technotes/tn/tn1150.html#BTrees

Mathur, A., Cao, M., Bhattacharya, S., Dilger, A., Tomas, A., Vivier, L. (2007). The new ext4 filesystem: current status and future plans. Proceedings of the Linux Symposium. Ottawa, Canada: Red Hat.

Bloom, B. H. (1970), Space/time trade-offs in hash coding with allowable errors, Communications of the ACM, 13 (7): 422-426