如果您是一名工程師，您很可能在完成搜索和查找算法時用過圖形的數(shù)據(jù)結(jié)構(gòu)。您是否也曾在機(jī)器學(xué)習(xí)問題上用過呢?

本教程分為兩部分：

• ***部分(也就是本篇啦!)： 用于無監(jiān)督學(xué)習(xí)的圖像

我們?yōu)槭裁葱枰P(guān)心圖形?

對于數(shù)據(jù)科學(xué)家，圖形是一個非常令人著迷的研究課題，標(biāo)記數(shù)據(jù)的方法在處理機(jī)器學(xué)習(xí)問題并不總是有效。圖形在無監(jiān)督上下文中非常強(qiáng)大，因為它們通過利用數(shù)據(jù)的基礎(chǔ)子結(jié)構(gòu)來充分利用您擁有的數(shù)據(jù)。

對于某些機(jī)器學(xué)習(xí)問題，圖形能幫您在沒有標(biāo)簽的地方獲得標(biāo)記數(shù)據(jù)!

我將會向您介紹一種被稱為社團(tuán)檢測(Community Detection)的方法去找到圖形中同一類數(shù)據(jù)點的聚類。我們將使用Spark圖形的幀數(shù)來處理我從2017年9月的Common Crawl dataset開始創(chuàng)建的大型網(wǎng)絡(luò)圖表。

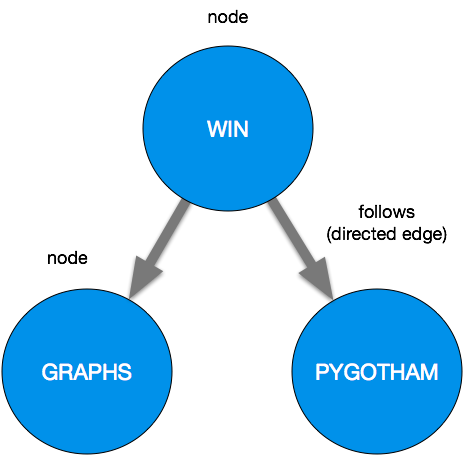
圖形的概念是用來表示對象配對關(guān)系的數(shù)據(jù)結(jié)構(gòu)。圖由節(jié)點(也成為頂點)和邊組成。他們可以是定向的或者不定向。例如，Twitter可以是一個有向圖;這種關(guān)系是單向的，僅僅是因為我關(guān)注另一個用戶，不意味著他們也關(guān)注了我! 

當(dāng)您為越來越多的頁面執(zhí)行此操作時，您會注意到子結(jié)構(gòu)的出現(xiàn)。 在真實的網(wǎng)絡(luò)數(shù)據(jù)上，這些子結(jié)構(gòu)可能非常龐大和復(fù)雜!

為什么圖形那么有用?

機(jī)器學(xué)習(xí)存在許多問題問題，其中標(biāo)簽(關(guān)于數(shù)據(jù)點是一類還是另一類的信息)不可用。 無監(jiān)督學(xué)習(xí)問題依賴于在數(shù)據(jù)點之間找到相似性以將數(shù)據(jù)分類為組或群集。 將此與受監(jiān)督的方法進(jìn)行對比，其中數(shù)據(jù)用適當(dāng)?shù)念悩?biāo)記，并且您的模型學(xué)習(xí)使用這些標(biāo)簽來區(qū)分類。

源網(wǎng)址: http://beta.cambridgespark.com/courses/jpm/01-module.html

當(dāng)您無法輕松獲取更多數(shù)據(jù)時，無監(jiān)督學(xué)習(xí)非常有用，因此您可以利用您擁有的數(shù)據(jù)獲得更多價值。 標(biāo)簽可能不可用; 即使它們是，它們可能太耗時或昂貴。 在機(jī)器學(xué)習(xí)問題開始時，我們也可能不知道我們正在尋找多少類對象!

這就是我們在工具箱中需要圖形的原因：

• 圖形允許我們在無人監(jiān)督的設(shè)置中從我們的數(shù)據(jù)中獲得更多價值。 我們可以從圖中獲得聚類。

無人監(jiān)督的學(xué)習(xí)與人類學(xué)習(xí)的方式?jīng)]有什么不同。你是如何首先學(xué)會區(qū)分狗和貓的? 我想對于大多數(shù)人來說，沒有人一生下來就會長大，還能用精確的分類術(shù)語來定義狗或貓是什么。你的父母也沒有給你一張包含數(shù)千只貓狗照片的語料庫，每張照片都標(biāo)有標(biāo)簽，并要求你畫出一個準(zhǔn)確劃分兩類動物的決定邊界。

如果你的童年和我的一樣，你可能遇到了幾只貓、幾只狗。 一直以來，你確定了兩種動物之間的顯著差異，以及每種動物的相關(guān)共同特征。 我們的大腦在從我們的環(huán)境中吸收信息，綜合這些數(shù)據(jù)，以及在我們生活中遇到的截然不同的事物之間制定共同點，我們的大腦實在是令人難以置信。

這是一個新聞網(wǎng)站下所有頁面的示例圖表。

聚類有許多令人激動的應(yīng)用。我的工作中遇到了一些例子：

• 為無法通過標(biāo)簽學(xué)習(xí)的數(shù)據(jù)集預(yù)測標(biāo)簽
• 生成受眾群體細(xì)分和分類分組
• 為類似的站點建立推薦人

發(fā)現(xiàn)異常

使用群集作為半監(jiān)督機(jī)器學(xué)習(xí)集合的一部分。 群集可以幫助您將已知標(biāo)簽擴(kuò)展到附近的數(shù)據(jù)點以增加訓(xùn)練數(shù)據(jù)大小，或者如果需要立即使用標(biāo)簽直到輔助系統(tǒng)對其進(jìn)行分類，則可以直接使用它們。

這是最關(guān)鍵的：在無人監(jiān)督的學(xué)習(xí)中，聚類是社團(tuán)，反之亦然。

圖形也是聚類!

***的區(qū)別是，您不依賴于工程特征，而是依賴圖中的底層網(wǎng)絡(luò)結(jié)構(gòu)來派生集群。 您可以使用圖中的邊來測量數(shù)據(jù)點之間的相似度，而不是使用預(yù)定義的距離度量。

之前我們提到了社團(tuán)(Community)，現(xiàn)在來大致介紹一下社團(tuán)這個概念。社團(tuán)定義不是***的，我們通常這樣來描述它：一個社團(tuán)是一個圖的子結(jié)構(gòu)，在這個子結(jié)構(gòu)中，結(jié)構(gòu)內(nèi)的結(jié)點相互之間聯(lián)系的比結(jié)構(gòu)外的結(jié)點連的更近，更緊密。而找到這些社團(tuán)(或者聚類)的過程叫做社團(tuán)檢測。

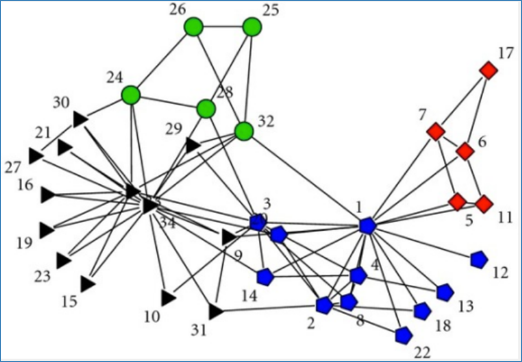
Zachary空手道俱樂部。圖片來自于KONECT，2017年4月。數(shù)據(jù)集來自于1977年Zachary的最初研究。

Zachary空手道俱樂部數(shù)據(jù)集對一個跆拳道俱樂部中各種會員之間的關(guān)系進(jìn)行了建模。有一次，俱樂部的兩名成員發(fā)生沖突，俱樂部最終分裂成多個社區(qū)。由圖可見，四個不同的社區(qū)由不同顏色表示。

可以思考一下無監(jiān)督聚類算法是如何進(jìn)行的。需要考慮到這一點，在你選擇的特征空間中，其中的數(shù)據(jù)點與別的數(shù)據(jù)點之間的距離并不是特別緊密。數(shù)據(jù)之間的距離越緊密，也就意味著他們之間相似度越高。 你可以根據(jù)數(shù)據(jù)點之間的距離矩陣，將具有相似屬性的數(shù)據(jù)放入同一個聚類中。

運用圖可以幫助你實現(xiàn)類似的集群，而無需像傳統(tǒng)集群那樣選擇數(shù)據(jù)特征。

每個淺藍(lán)色點代表單個網(wǎng)頁，即節(jié)點

每條深藍(lán)色線代表兩個頁之間的鏈接，即邊

新聞網(wǎng)站的子頁面結(jié)構(gòu)由我使用Gephi生成。

即使在此級別，您也可以看到頁面的密集群集或社團(tuán)。 您可以發(fā)現(xiàn)更高度中心性的節(jié)點(頁面都具有鏈接到它們的大量其他頁面)

如果一個站點的連接都如此密集，想象一下我們可以從成千上萬的站點中挖掘出什么!

等等，為啥這種方法能行得通呢?

讓我們繼續(xù)往下學(xué)習(xí)。我們需要做出哪些假設(shè)，來讓我們依靠社區(qū)檢測來查找具有相似屬性的節(jié)點?

最重要的一個是：

結(jié)點之間的連接線并不是隨機(jī)的。

如果你的圖是隨機(jī)的話，那么根本不會行得通的。但是現(xiàn)實生活中大多數(shù)的圖并不是隨機(jī)的。結(jié)點相互之間的連接關(guān)系是存在某種相關(guān)性的。以下兩個原則會解釋其中的原因：

1. 相互影響原則。相互連接在一起的結(jié)點更容易共享或者傳遞特征。試著想象一下，當(dāng)你的幾個朋友嘗到了Spark帶來的便利的時候，你作為與他們相互聯(lián)系緊密的人，也有可能會開始學(xué)著使用Spark。“我所有的朋友都在用，所以我也要用”
2. 同質(zhì)相吸原則。結(jié)點之間有著一個相類似的特征，或者有某些關(guān)聯(lián)的時候，很有可能會連接在一起。例如，如果你和我都喜歡用Python而且都喜歡圖，用圖來表示的話，我們很有可能是兩個相互連接的結(jié)點。這也叫做正匹配，“物以類聚”。

在現(xiàn)實生活中，這兩個原則會相互作用!

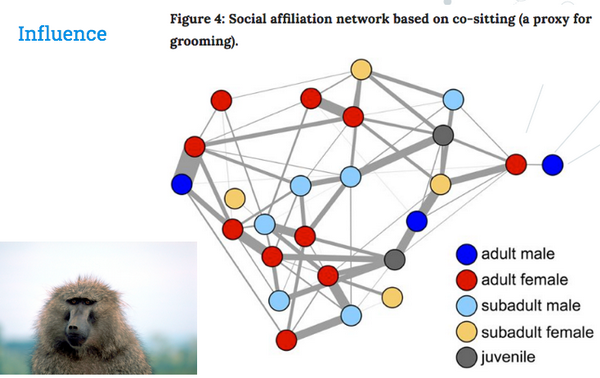
研究人員利用這些現(xiàn)象可以對圖中的一些有趣的問題建模。例如，F(xiàn)arine et al通過動物之間強(qiáng)烈關(guān)聯(lián)性預(yù)測了狒狒的位置——對行為生態(tài)學(xué)產(chǎn)生了很好的影響。

Farine, Damien R., et al“最近鄰居和長期分支機(jī)構(gòu)都能預(yù)測野生狒狒集體行動期間的個體位置。”科學(xué)報告6(2016)：27704

同質(zhì)相吸原則經(jīng)常用于社交網(wǎng)絡(luò)研究。Adamic和Glance在2004年大選期間對政治博客進(jìn)行了一項引人入勝的研究。 他們用圖表的方式，顯示了不同的博客如何相互引用;藍(lán)色節(jié)點代表自由博客，紅色節(jié)點是保守的博客。 也許不出所料，他們發(fā)現(xiàn)博客傾向于引用同樣政治傾向的其他博客。

Adamic，Lada A.和Natalie Glance。 “政治博客圈和2004年美國大選：區(qū)分了他們的博客。”第三屆國際鏈接發(fā)現(xiàn)研討會論文集。ACM，2005年。

即使在個人層面上，同質(zhì)相吸原則也是有道理的。 機(jī)會是你自己的朋友網(wǎng)絡(luò)由可能與你年齡相同，住在同一個城鎮(zhèn)，有相同的愛好，或去同一所學(xué)校的人組成! 在工作中，你是一個活生生同質(zhì)相吸原則的例子。不要畏懼，大膽將它加入到簡歷中!

我們已經(jīng)介紹了圖是怎么運用數(shù)據(jù)中基本的網(wǎng)絡(luò)特性來生成聚類。在互聯(lián)網(wǎng)中，這些聚類對于推薦系統(tǒng)、觀眾分類、以及異常檢測等等都有重大意義。

在第二部分(鏈接傳送門)，我們會將對社團(tuán)檢測技術(shù)進(jìn)行深入研究，并且學(xué)著怎么利用常用的爬蟲數(shù)據(jù)集，從網(wǎng)頁的圖狀結(jié)構(gòu)中得到聚類。