十個技巧,讓你成為“降維”專家
大數據文摘出品
來源:PLOS
編譯:啤酒泡泡、劉兆娜、李雷、sirin、邢暢、武帥、錢天培
在分析高維數據時,降維(Dimensionality reduction,DR)方法是我們不可或缺的好幫手。
作為數據去噪簡化的一種方法,它對處理大多數現代生物數據很有幫助。在這些數據集中,經常存在著為單個樣本同時收集數百甚至數百萬個測量值的情況。
由于“維度災難”(curse of dimensionality)的存在,很多統計方法難以應用到高維數據上。雖然收集到的數據點很多,但是它們會散布在一個龐大的、幾乎不可能進行徹底探索的高維空間中。
通過降低數據的維度,你可以把這個復雜棘手的問題變得簡單輕松。除去噪音但保存了所關注信息的低維度數據,對理解其隱含的結構和模式很有幫助。原始的高維度數據通常包含了許多無關或冗余變量的觀測值。降維可以被看作是一種潛在特征提取的方法。它也經常用于數據壓縮、數據探索以及數據可視化。
雖然在標準的數據分析流程中已經開發并實現了許多降維方法,但它們很容易被誤用,并且其結果在實踐中也常被誤解。
本文為從業者提供了一套有用的指南,指導其如何正確進行降維,解釋其輸出并傳達結果。
技巧1:選擇一個合適的方法
當你想從現有的降維方法中選擇一種進行分析時,可用的降維方法的數量似乎令人生畏。事實上,你不必拘泥于一種方法;但是,你應該意識到哪些方法適合你當前的工作。
降維方法的選擇取決于輸入數據的性質。比如說,對于連續數據、分類數據、計數數據、距離數據,它們會需要用到不同的降維方法。你也應該用你的直覺和相關的領域知識來考慮收集到的數據。通常情況下,觀測可以充分捕獲臨近(或類似)數據點之間的小規模關系,但并不能捕獲遠距離觀測之間的長期相互作用。對數據的性質和分辨率的考慮是十分重要的,因為降維方法可以還原數據的整體或局部結構。一般來說,線性方法如主成分分析(Principal Component Analysis, PCA)、對應分析(Correspondence Analysis, CA)、多重對應分析(Multiple Correspondence Analysis, MCA)、經典多維尺度分析(classical multidimensional scaling, cMDS)也被稱為主坐標分析(Principal Coordinate Analysis, PCoA) 等方法,常用于保留數據的整體結構;而非線性方法,如核主成分分析(Kernel Principal Component Analysis, Kernel PCA)、非度量多維尺度分析(Nonmetric Multidimensional Scaling, NMDS)、等度量映射(Isomap)、擴散映射(Diffusion Maps)、以及一些包括t分布隨機嵌入(t-Distributed Stochastic Neighbor Embedding, t-SNE)在內的鄰近嵌入技術,更適合于表達數據局部的相互作用關系。NE技術不會保留數據點之間的長期相互作用關系,其可視化報告中的非臨近觀測組的排列并沒有參考價值。因此,NE的圖表不應該被用于數據的大規模結構的推測。有關線性和非線性降維方法的綜述可分別參考如下兩篇文章。
相關鏈接:
- https://scholar.google.com/scholar?q=Linear+Dimensionality+Reduction%3A+Survey%2C+Insights%2C+and+Generalizations+Cunningham+2015
- https://arxiv.org/abs/1803.02432)
如果你的觀測值帶有類別標簽,并且你的目標是將觀測值分類到已知的與其最匹配的類別中去時,則可以考慮使用監督降維技術。監督降維技術包括偏最小二乘法(Partial Least Squares, PLS)、線性判別分析(Linear Discriminant Analysis, LDA)、近鄰成分分析(Neighborhood Component Analysis)和Bottleneck神經網絡分類器。與之前提到的非監督降維方法不同的是,非監督方法并不知道觀測值所屬的類別,而監督降維方法可以直接利用類別信息把相同標簽的數據點聚集到一起。
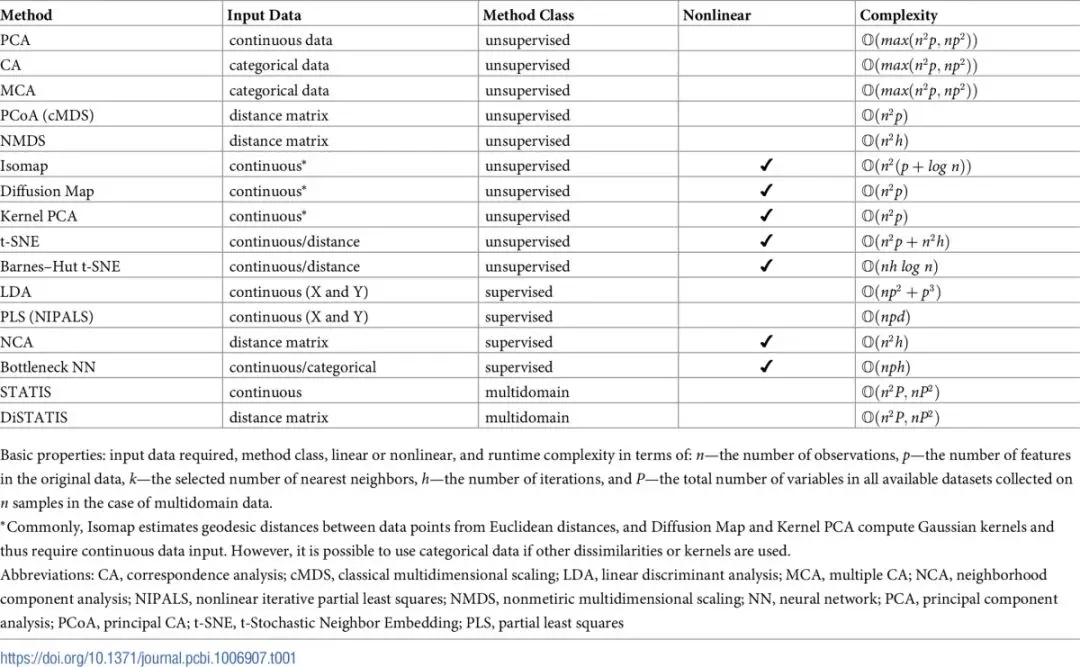
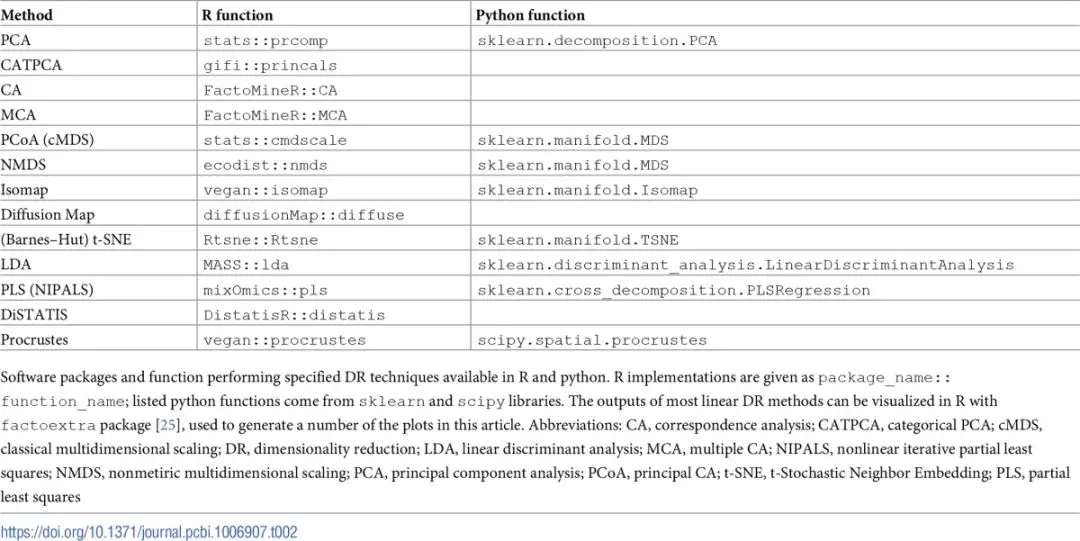
對于收集多領域數據的情況,例如基因表達、蛋白質組學以及甲基化的數據,你可能需要先將降維技術分別應用到每張數據表中,然后再使用普魯克變換(Procrustes transformation,相關鏈接:https://onlinelibrary.wiley.com/doi/abs/10.1002/bs.3830070216)或是其他可以將多個數據集整合的方法,如用于多個表的聯合分析方法(稱為STATIS);和用于多個距離矩陣的聯合分析(稱為DisTATIS,相關鏈接:)(詳細信息請參考技巧9)。表1給出了降維技術的基本屬性的分類和總結。為了幫助從業者,我們也把本文討論過的降維技術的實現方法總結到表2中。
表1.降維方法
表2.案例實現
技巧2:對連續型和計數型輸入數據進行預處理
在應用降維技術之前,先對數據進行適當的預處理通常十分必要。例如,數據中心化,變量的觀測值減去該變量觀測值的平均值,就是主成分分析處理連續數據的必要步驟,并且在大多數標準實現中是默認應用的。另一種常用的數據轉換方法則是縮放,將變量的每一個測量值乘以一個縮放因子,使得縮放后的變量的方差為1。縮放處理保證了每一個變量都產生等價的貢獻,這對于那些包含具有高度可變范圍或不同單位異構的數據集尤其重要,如患者臨床數據,環境因素數據等。
當所有變量的單位都相同時,如在高通量測定中,則不建議進行方差標準化,因為這會導致強信號特征的收縮以及無信號特征的膨脹。根據具體的應用、輸入數據的類型、使用的降維方法,可能會需要用到其他的數據變換方法。舉個例子,如果數據的變化具有可乘性,比如你的變量測定的是百分比的增加或減少,那么你應該考慮在使用主成分分析之前對該其進行對數變換。在處理基因組測序數據時,需要先解決兩個問題,才能進行數據降維。***個問題:每個序列樣本都有一個大小不同的庫(也稱為測序深度),這是一個人為的區分觀測值的討厭參數。為了讓觀測值之間可比較,需要先使用特定的方法(如DESeq2,edgeR)估算出一個樣本大小的因子,然后用對應的樣本中的每個觀測值去除以這個因子,將樣本標準化;第二個問題:分析數據往往會表現出均值-方差的正相關趨勢,即高均值意味著高方差。該情況下,需要使用方差穩定變換去調節這種影響,使其避免傾向于較多的特征。對于那些服從負二項分布的計數數據,如序列計數,則推薦使用反雙曲函數正弦變換或者類似的方法[28-30]。對于高通量數據,樣本標準化和方差穩定化相結合的辦法是高吞吐量數據的有效的預處理步驟。
技巧3:正確處理含有分類變量的輸入數據
在許多情況下,可用的測量不是數值的,而是定性的或分類的。對應的數據變量表示類別,而不是數值數量,例如表型、隊列成員、樣本測序運行、調查應答評級等。當關注點是兩個分類變量的水平(不同的值)之間的關系時,對應分析(CA)會用于分析列聯表中類別的共現頻率。如果有兩個以上的分類變量時,多重對應分析(MCA)可以用來分析觀測點之間的關系以及變量類別之間的聯系。多重對應分析是對應分析的泛化,其本質就是將對應分析應用到一個將分類變量獨熱編碼(one-hot encoding)的指示矩陣中。當輸入數據既包括數值變量又包括分類變量時,則有兩種策略可用。如果只有少數幾個分類變量,那么可以對數值變量進行主成分分析處理,分類變量每個水平的平均值則可以通過投影為補充點(不加權)。另一方面,如果這個混合數據集包含大量的分類變量,則可以使用多因子分析法(MFA)。這個方法是對數值變量使用主成分分析,對分類變量使用多因子分析,然后加權并合并變量組的結果。
處理分類或混合數據的另一種方法是采用“***量化”的思想,利用PCA(即主成分分析法,下文直接采用PCA)對變量進行轉換。由于目標是***化方差,故傳統PCA只能對數值型變量實行降維,不能作用在分類變量上。要想對定類(無序)或定序(有序)分類變量實行PCA降維,一種方式是將方差替換成由基于各類別的頻數計算出的卡方距離(如在對應分析中),或者可以在執行PCA之前進行適當的變量變換。這里提供兩種變量變換的方式:一種是將分類變量虛擬化編碼為二分類特征;另一種是使用***縮放分類主成分分析法(CATPCA)。***縮放法的原理是將原有的分類變量進行類別量化,從而轉換成新變量的方差***化。通過***縮放可以將分類主成分分析轉化成***化問題,通過成分得分、成分加載和成分量化的交替變換,經過不斷迭代使得量化后的數據和主成分之間的平方差最小。
***縮放的一個優點是它無需預先假定變量之間存在線性關系。 實際上,即使輸入數據都是數值型時,分類主成分分析法在處理變量之間非線性關系的能力也很重要。 因此,當變量之間存在非線性關系且標準PCA只能解釋方差的低比例時,***縮放法提供了可能的補救措施。
技巧4:使用嵌入方法降低輸入數據的相關性和相異性
在既沒有可用的定量特征也沒有可用的定性特征時,用相異性(或相關性)度量的數據點之間的關系可以采用低維嵌入的方法進行降維。即使可以進行可變測量,計算相異性和使用基于距離的方式也是一種有效的方法。但要,你要確保你選擇了一個能夠***地概括數據特征的相異度量標準。例如,如果源數據是二進制的,那就不能使用歐幾里德距離,這時選擇曼哈頓距離更好。但是,如果特征是稀疏,則應該優選Jaccard距離。
經典多尺度分析(cMDS)、主坐標分析(PCoA)和非度量多尺度分析(NMDS)使用成對數據之間的差異性來找到歐幾里德空間中的嵌入,從而實現對所提供距離的***近似。盡管經典多尺度分析(cMDS)是一種類似于主成分分析(PCA)的矩陣分解方法,但非度量多尺度分析(NMDS)是一種力求僅保留相異性排序的優化技術。當對輸入距離值的置信度較低時,后一種方法更適用。當相異性數據是非標準的、定性數據時,可以使用更專業的序數嵌入方法,可以參考Kleindessner和von Luxburg的詳細討論。當使用基于優化的多維縮放(MDS)時,可以選擇僅通過局部交互將最小化問題限制在從數據點到其鄰居(例如,k-最近鄰)的距離。該方法稱為“局部”MDS。
相異性也可以用作t分布隨機嵌入(t-SNE)的輸入。與局部MDS類似,t分布隨機嵌入(t-SNE)專門用于于表示短程交互。然而,該方法通過使用小尾的高斯核函數將所提供的距離轉換為鄰近度量,從而以不同的方式實現了局部性。目前,已經開發了一種基于神經網絡的詞向量(word2vec) 方法,該方法使用相似性數據(共現數據)來生成連續歐幾里德空間中的對象的向量嵌入。 事實證明,這項技術在從由文本語料庫衍生的數據中生成單詞嵌入方面非常有效。 但是,這些高級計算方法的魯棒性尚未在很多生物數據集上進行廣泛測試。
技巧5:有意識地決定要保留的維數
在對數據進行降維時,關鍵問題是選擇一個合適的新維度的數量。這一步決定了能否在在降維后的數據中捕獲到感興趣的信號,降維時維度數量的選擇在統計分析或機器學習任務如聚類之前的數據預處理步驟中尤為重要。即使你的主要目標是進行數據可視化,但是由于可視化時一次只能顯示兩個或三個軸,你仍要選擇降維后要保留的合適的新維度數量。例如,如果前兩個或三個主成分對方差的解釋不足時,就應該保留更多的成分,在這種時候就需要對成分的多種組合進行可視化(例如,成分1與成分2,成分2與成分4,成分3與成分5之間的對比等)。在某些情況下,***信息是一個復雜的因子,并且有用的信息被高階成分捕獲。在這種情況,就必須使用高階成分來顯示其模式。
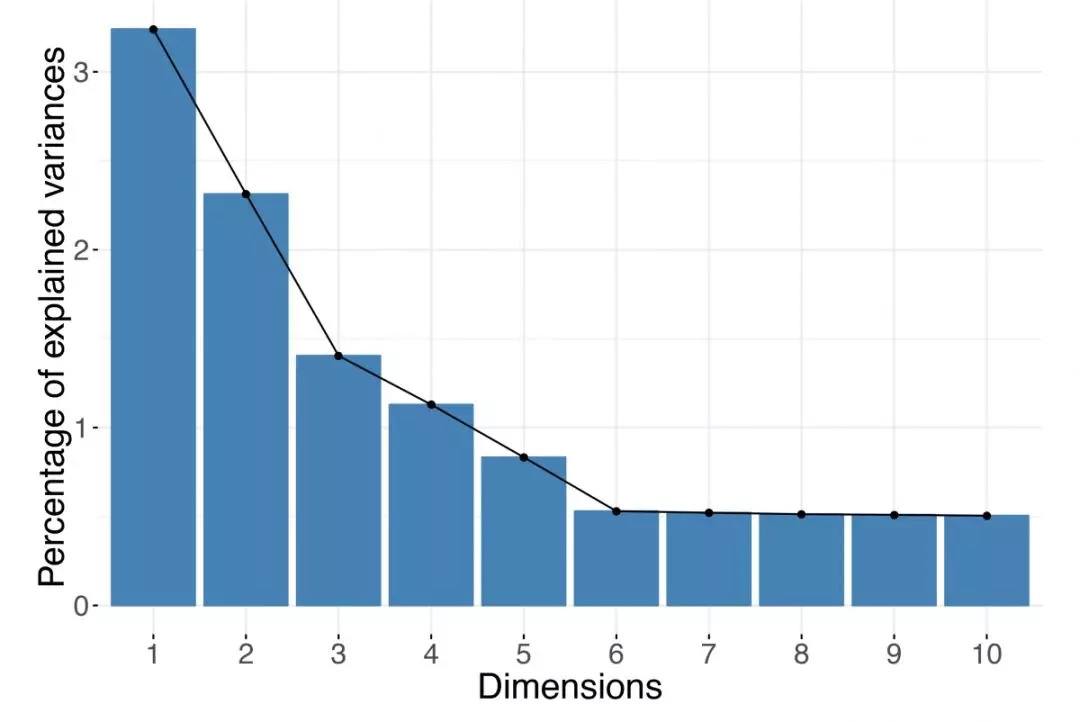
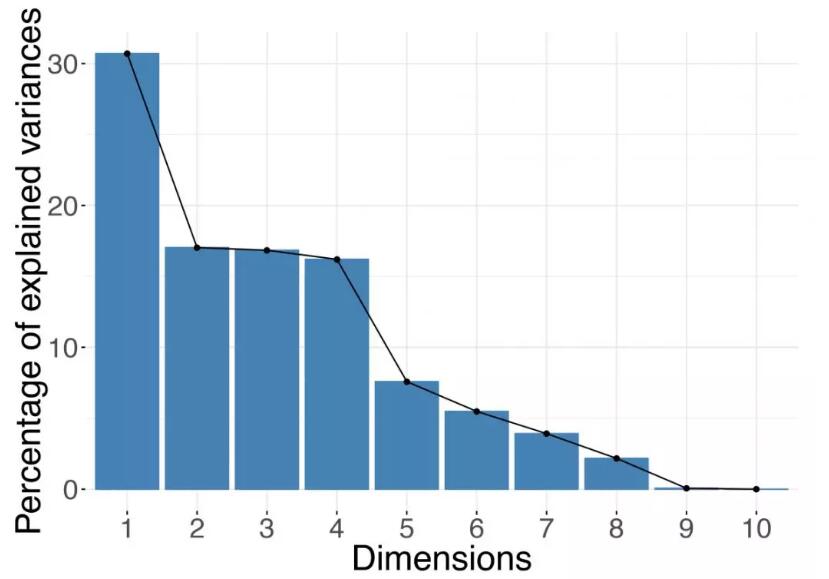
要保留的***維度數很大程度上取決于數據本身。在了解數據之前,您無法確定正確的輸出維度數。請記住,***的維度數量是數據集中記錄數(行數)和變量數(列數)的最小值。例如,如果你的數據集包含10,000個基因的表達式,但只有10個樣本,則降維時行不能超過10個(如果輸入數據已居中,則為9個)。對于基于光譜分解的降維方法,例如主成分分析(PCA)或主坐標分析(PCoA),你可以根據特征值的分布情況來進行維度的選擇。在實踐中,人們在做決定時通常依賴于碎石圖“scree plot”(見圖1)和“肘部法則(也稱為拐點法則)”。碎石圖直觀展示了輸出結果中的每個特征的值,或者等價地展示,每個特征如一個成分對方差的解釋比例。通過觀察圖形,你能夠找到一個拐點,這個位置的特征的值比它之前緊挨著它的位置的值顯著下降。或者,你可以觀察特征值的直方圖,并從所有特征中找出“脫穎而出”的值比較大的特征。馬爾琴科—巴斯德分布(Marchenko-Pastur distribution)在形式上近似地模擬了大量隨機矩陣的奇異值的分布。因此,對于記錄數量和特征數量都很大的數據集,你使用的規則是只保留擬合的馬爾琴科—巴斯德分布支持之外的特征值;但請記住,這僅在數據集至少包含數千個樣本和數千個特征的情況下才可用。
圖1.碎石圖
根據優化方法,特征值可用于確定保留多少維度是充分的。根據“肘部規則”,可以選擇要保留的維度的數量。在上面的示例中,你應該保留前五個主成分。
對于非優化方法,通常在降維之前預先指定成分的數量。當使用這些方法時,可以通過迭代的方法不斷增加維度的數量,并評估每次迭代中增加的維度是否能夠使損失函數顯著減小,來最終選擇降維時要保留的成分的數量。例如t分布隨機嵌入的情況下,由KL散度(KL)定義的輸入變量和輸出變量之間的轉換概率。理想情況下,你肯定愿意你的發現(例如,可視化中觀察到的模式)對維度數量的選擇具有魯棒性。
技巧6:在可視化時使用正確的寬高比
可視化是數據探索過程的重要組成部分。因此,你生成的DR圖能否準確反映降維方法的輸出至關重要。關于可視化,一個重要但經常被忽視的屬性是其寬高比。2D(和3D)圖的高度和寬度(以及深度)之間的比例關系可以強烈影響你對數據的感知; 因此,DR圖應遵循與顯示的輸出軸所解釋的相對信息量相一致的寬高比。
在PCA或PCoA的情況下,每個輸出維度都具有相應特征值,該特征值與其所代表的方差值成比例。如果圖表的高寬比是任意的,則不能獲得數據的完整圖像。由于用于分析生物數據的流行軟件通常默認生成方形(2D)或立方形(3D)的圖形,因此高寬相等的二維PCA圖很常見,但也經常使人產生誤解。其實,PCA圖表的高寬比應與相應特征值之間的比率相一致。由于特征值反映了相關主成分坐標的變化,因此只需要確保在圖表中,一個PC方向上的單位長度與另一PC方向單位長度相同。(如果你使用ggplot2 R軟件包來生成圖表,添加+ coords_fixed(1)將確保正確的寬高比。)
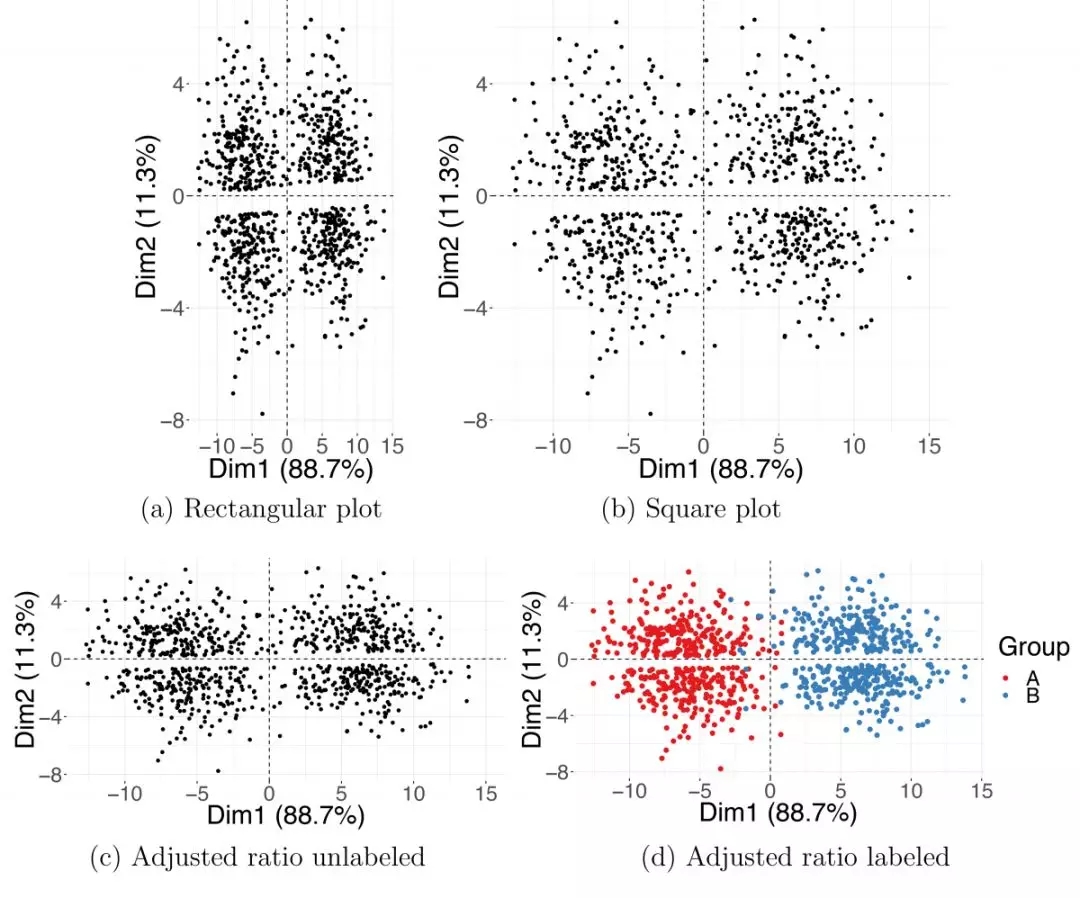
我們用圖2所示的模擬示例來說明寬高比問題。在矩形(圖2A)和正方形(圖2B)圖中,寬高比與PC1和PC2坐標的方差不一致; 結果是明顯地將數據點(錯誤地)分組到圖表的頂部和底部。相反,圖2C,垂直兩軸的長度比與相應特征值之間的比率一致,因此可以顯示正確的分組,與真實的分類一致。
圖2. PCA圖的寬高比
兩個模擬高斯群集投射在***和第二個主成分上。矩形(a)和方形(b)圖中的寬高比不正確。將(c,d)圖中的寬高比進行校正,其中調整圖表的高度和寬度以匹配PC1和PC2坐標中的方差。(d)圖中顯示的顏色表示真正的高斯分組關系。Dim1,維度1; Dim2,維度2; PC,主成分; PCA,主成分分析。
在許多基于優化的降維方法中,維度的排序沒有意義。例如,在t-SNE的情況下,你可以在生成新的數據表示之前選擇輸出維度的個數(通常為兩個或三個)。與主成分不同,t-SNE的各維度是無序且同等重要的,因為它們在通過優化算法的最小化損失函數中具有相同的權重。因此,對于t-SNE,通常的做法是使投影圖形為正方形或立方形。
技巧7:理解新維度的含義
許多線性DR方法,包括PCA和CA,都為觀測值和變量提供了約化表示。特征映射(Feature maps)或相關性圓圖(correlation circles)可用于確定哪些原始變量彼此相互關聯,或與新生成的輸出維度相關聯。特征向量之間的夾角或與PC軸之間的夾角包含如下信息:兩個夾角大約在0°(180°)的向量,其相應的變量間的關系也是是密切正(或負)相關的,而具有90°夾角的兩個向量可以看作相對獨立的。
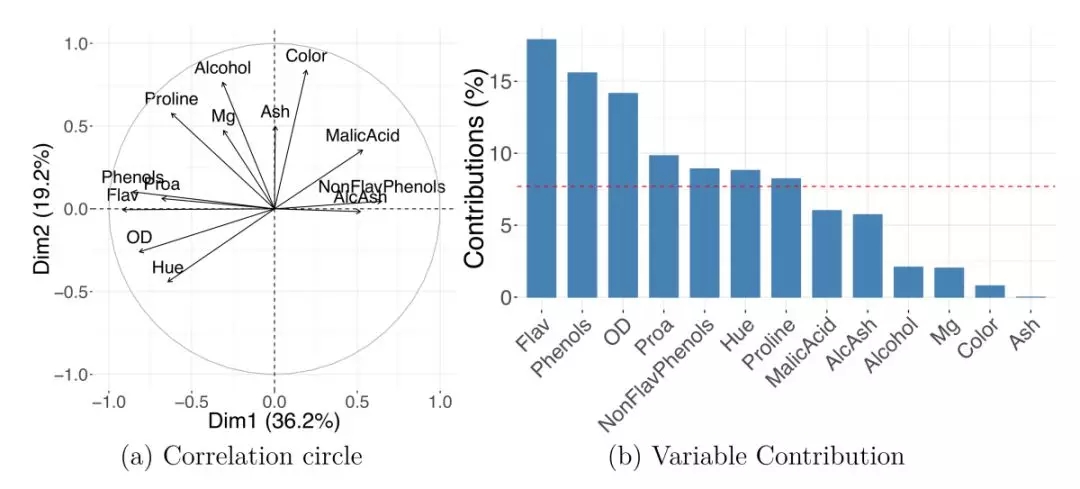
圖3A展示了具有變量投影的縮放坐標的相關性圓圖。該圖表明PC1的高值表示“Flav”(類黃酮)和“Phenols”(總酚類)中的低值以及“Malic Acid”( 蘋果酸)和“AlcAsh”(灰分的堿度)中的高值。此外,“AlcAsh”(灰分的堿度)水平似乎與“NonFlav Phenols”(非黃烷類酚)密切負相關并且與“Alcohol”(酒精)水平無關。
圖3.變量的投影
葡萄酒數據集上的PCA顯示了怎樣用變量的表示來理解新維度的含義。相關性圓圖(a)和PC1貢獻圖(b)。AlcAsh,灰分的堿度; Dim1,維度1; Dim2,維度2; Flav,黃酮類; NonFlav Phenols,非黃烷類酚類; OD,OD280 / OD315稀釋的葡萄酒; PC,主成分; PCA,主成分分析; Phenols,總酚類; Proa,原花青素。
可以用貢獻條形圖來展示原始變量對新維度的重要性。變量對給定新軸線的貢獻為其坐標平方(在此軸線上)與相應的所有變量總和之比; 該比率通常用百分比表示。許多程序將變量的貢獻作為標準輸出; 不僅可以為單個軸線定義貢獻值,還可以通過對選定成分相對應的值求和為多個DR軸定義貢獻值。圖3B顯示的是變量對PC1的百分比貢獻; 請注意,百分比貢獻不包含關聯方向的信息。當使用高通量分析等高維數據集時,數千個或更多變量的貢獻條圖就不實用了; 相反,你可以限制圖表的取值,僅顯示具有***貢獻的前幾個(例如,20個)特征。
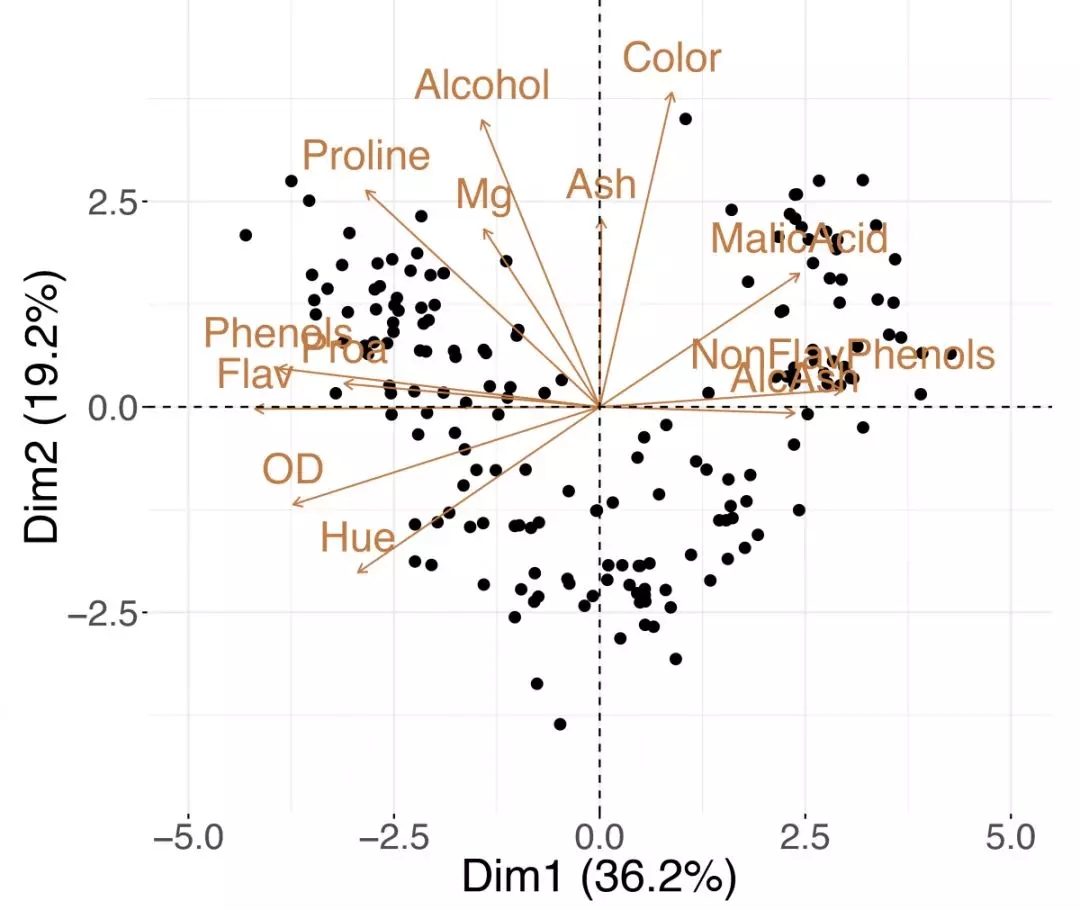
變量和觀測值可以包含在同一圖形中 - 稱為“雙時隙”。這個術語是由Kuno Ruben Gabriel 于1971年創造的,但是Jolicoeur和Mosimann早在1960年就提出了類似的觀點。如圖4所示的雙時隙圖可以同時展示數據樣本和特征的趨勢; 同時查看兩者,你可能會發現類似(近距離)觀察的組,這些觀測值對于某些測量變量具有高值或低值(更多詳細信息,請參見技巧8)。
圖4. 主成分雙標圖
葡萄酒數據集的單時隙圖將樣本和變量的投影組合到前兩個主成分中。AlcAsh,灰分的堿度; Dim1,維度1; Dim2,維度2; Flav,黃酮類; NonFlav Phenols,非黃烷類酚類; OD,OD280 / OD315稀釋的葡萄酒; PCA,主成分分析; Phenols,總酚類; Proa,原花青素。
技巧8:找到隱藏的信號
降維的主要目標是壓縮數據,同時保留大部分有意義的信息。數據壓縮簡化了理解數據的過程,因為簡化的數據表達可以更有效地獲知數據變化的主要來源。其目的是找到能夠成功揭示數據底層結構的“隱藏變量”。最常見的潛在模式是離散集群或連續梯度。
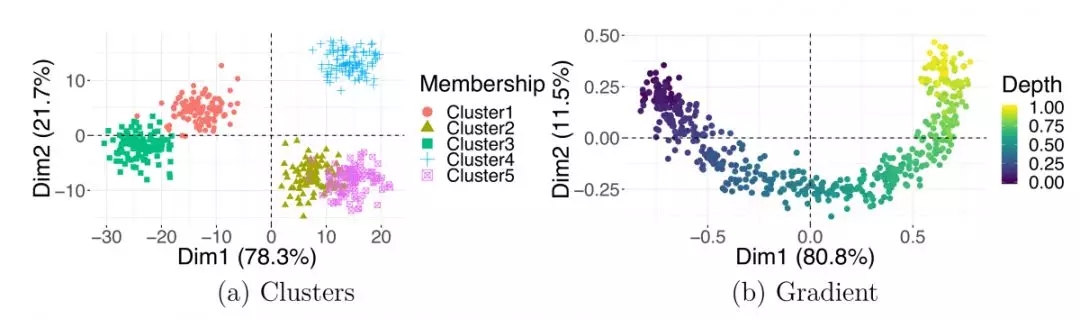
在前一種情況下,相似的觀察結果遠離其他群體。圖***顯示了一個模擬集群數據集的例子。當執行聚類分析時,目的是分析樣本的組別,通常的做法是首先應用主成分分析。更具體地說,實踐者經常使用一組頂部的PC(例如,50個)作為集群算法的輸入。主成分分析所帶來的維度的減少是一個數據降噪步驟,因為頂部特征向量應該包含所有感興趣的信號。遺憾的是,該屬性并未擴展到所有降維方法。鄰域嵌入技術(如t-SNE)產生的輸出不應用于聚類,因為它們既不能保持距離也不能保持密度——這兩個量在解釋聚類輸出時都非常重要。
圖5.潛在結構
主成分分析圖中的觀測值可分為組(a)或遵循連續梯度(b)。Dim1,維度1;Dim2,維度2;PCA即主成分分析法
與離散集群不同,數據中的連續變化不太容易被識別。了解如何識別和準確解釋潛在梯度非常重要,因為它們經常出現在與未知連續過程相關的生物數據中。當數據點沒有分離成不同的聚類,而是從一個極端向另一個極端逐漸移動時,梯度就出現了;它們通常在數據降維的可視化中以平滑曲線的形式出現。值得注意的是,當PCA和cMDS(PCoA)應用于涉及線性梯度的數據時,數據點通常以呈現出馬蹄形或弓形。當相關特征向量由于計算中使用的數據協方差或距離矩陣的性質而呈現特定形式時,特別是當這些矩陣可以表示為中心對稱的Kac-Murdock-Szego矩陣時,PCA和cMDS圖中就會出現“馬蹄效應”。
你可以在圖5B中看到具有潛在梯度的模擬數據的這種模式的示例。當觀測隨著時間的推移而進行時,經常會遇到連續躍遷;例如,細胞發育的文獻中有大量介紹分析pseudotime的方法的文章,pseudotime是細胞分化或發育過程中觀察到的一種梯度。可以有多個梯度影響數據,在不同方向可以記錄一個穩定的變化。然而,觀測到的連續梯度背后的變量可能是未知的。在這種情況下,你應該通過檢查任何可用的外部協變量的值之間的差異,集中精力找出梯度端點(極值)處的觀測值之間的差異(參見技巧7)。否則,你可能需要收集關于數據集中樣本的其他信息,以研究這些差異的解釋。
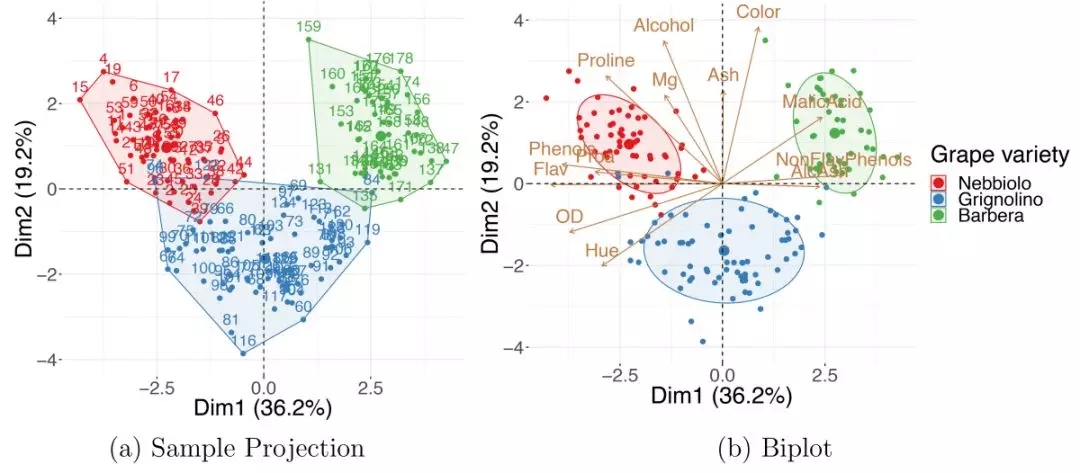
其他連續測量值(不用于數據降維計算的測量值)通常是根據數據集中包含的觀測值獲取的。額外的信息可以用來提高對數據的理解。使用外部協變量的最簡單和最常見的方法是將它們包含在數據降維的可視化中——它們的值被編碼為繪圖上相應點的顏色、形狀、大小甚至透明度。這方面的一個例子如圖6A所示:葡萄酒屬性數據集的主成分分析嵌入,其中數據點按葡萄酒類別著色,這是數據降維所忽視的一個變量。觀察到的葡萄酒分組表明,用于降維的13種葡萄酒特性可以很好地表征葡萄酒類別。“葡萄酒數據集”可從加州大學歐文分校(University of California Irvine ,UCI)機器學習數據庫中獲取。
圖6.使用外部信息
(a)對葡萄酒數據集的PCA樣本投影顯示,根據葡萄酒的特性,葡萄酒往往與葡萄品種分類一致:內比奧羅(Nebbiolo)、格里諾利諾(Grignolino)和巴貝拉(Barbera)。(b)主成分分析雙標圖(biplot)可以用來找出哪一組葡萄酒具有較高的哪一種性質。Dim1,維度1;Dim2,維度2;主成分分析。
有時,根據新計算的特征直接繪制外部變量是顯示數據變化趨勢的有效方法。例如,連續變量(例如患者的年齡或體重)的散點圖與所選輸出維度的坐標之間的關系顯示所選協變量與新特征之間的相關性。如果外部信息是分類的而不是連續的,則可以為變量的每一級生成PC坐標的箱線圖(例如PC1、PC2或其他)。
外部信息也可以合并到雙標圖(bioplots)中。圖6B顯示了將觀察到的外部信息與根據原始變量對新坐標軸的解釋相結合 (如技巧7所述)。你可以發現“Barbera”葡萄酒往往含有較高的“蘋果酸”和較低的“黃烷酸”,而“Grignolinos”往往含有較低的“灰分”和“酒精”含量。
此外,外部信息可用于發現批次效應。批次效應是技術或系統的變異來源,它掩蓋了感興趣的主要信號。它們經常出現在測序數據中,其中來自相同測序運行(lane)的樣品聚集在一起。因為批次效應會混淆感興趣的信號,所以在進行進一步的下游分析之前,***檢查它們的存在,如果發現,則將其移除。你可以通過數據降維嵌入圖來檢測技術或系統變化,該嵌入圖中的數據點按批次成員資格進行著色,例如按測序運行、籠號、研究隊列進行著色。如果發現批次效應,你可以通過移動所有觀察值來移除它,方法是每個批處理的質心(組的重心)移動到繪圖的中心(通常是坐標系的原點)。
技巧9:利用多域數據
有時,我們對于對于同一組樣本,會獲取一組以上的測量值;例如,高通量基因組研究就經常涉及到多個領域的數據。對于相同的生物樣品,我們可以獲取到它的微陣列基因表達、微核糖核酸表達、蛋白質組學和脫氧核糖核酸甲基化等一系列數據。通過集成多個數據集,你可以獲得更精確的高階交互表示,并評估與之相關的可變性。由于不同區域的數據受到不同的變動率或波動率的影響,樣本往往表現出不同程度的不確定性。
處理“多域”數據(也可稱作為“多模態”、“多向”、“多視角”或“多組學”數據)的一種方法是分別對每個數據集執行數據降維,然后使用普魯克變換將它們對齊在一起—平移、縮放和旋轉的組合,以盡可能緊密地將不同數據結構對齊。許多更先進的方法也被開發出來,例如STATIS和DiSTATIS分別是PCA和經典MDS的推廣。這兩種方法都用于分析在同一組觀測數據上獲取的多個數據集,并且都基于將數據集組合成一個稱為“折中”的共同共識結構的思想。
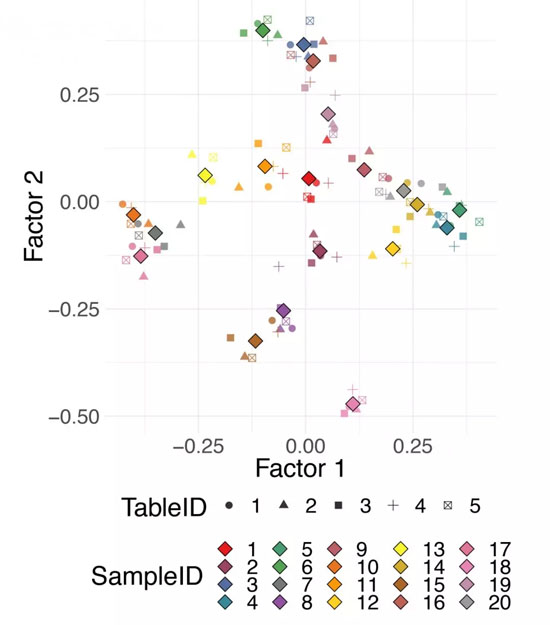
所以的數據集都可以投影到這個共識空間。單個數據集的投影可以幫助觀察來自不同領域的數據所描述的觀察中的不同模式。圖7顯示了DiSTATIS在5個模擬距離表上對20個合成數據點的使用示例。不同的顏色對應不同的數據點,不同的形狀對應不同的距離表。數據表之間的“折中點”用較大的菱形標記表示。有關多表數據分析的詳細研究,重點是生物多組學數據集,可以請參見Meng及其同事的相關研究結果。
圖7.多域數據
為同一觀測值定義的多個距離表上的DiSTATIS。可以從不同的數據類型(例如,基因表達、甲基化、臨床數據)或從已知的數據生成分布中重新采樣的數據來計算多個距離。
技巧10:檢查結果的魯棒性并量化不確定性
如圖8所示,對于某些數據集而言,PCA的 PC定義是不明確的,即連續兩個或多個PC可能具有非常相似的方差,并且相應的特征值也幾乎完全相同,如圖8所示。盡管由這些分量共同組成的子空間是有意義的,但特征向量(即PC)并不能單獨提供信息,而且它們的載荷也不能單獨解釋,因為即使是一個觀察點中的微小變化也會導致完全不同的特征向量集。在這種情況下,我們說這些pc是不穩定的。相似特征值對應的維度應該一起理解而不能單獨解釋。
圖8.不穩定的特征值
當多個特征值近乎相等時,PCA表示是不穩定的。PCA,principal component analysis,即主成分分析。
使用需要指定參數的技術時,還應根據不同的參數設置檢查結果的穩定性。例如,在運行t-SNE時,你需要為困惑度選擇一個值,不同的值甚至可能定性地改變結果。當困惑度被設置為非常小的值時,常會形成“人工聚類”。不應該使用t-SNE目標函數的值即KL散度作為選擇“***困惑度”的標準,因為隨著困惑度值的增加,KL散度總是單調減小。對于t-SNE,Cao和Wang在提出了用于選擇困惑度的貝葉斯信息準則(BIC)類型規則。然而由于t-SNE的穩定性理論還沒有開發出來,在實踐中,應該針對一系列輸入參數重復降維計算,并直觀地評估所發現的模式在不同規格中是否一致。尤其是當困惑度值的微小增加導致聚類模式消失時,你得到的分類可能只是參數選擇不合適帶來的錯誤結果。
另一個需要關注的問題是方法面對異常值時的穩定性。一般來說,遠離中心的觀察點對PC的影響要大于靠近中心的觀察點;有時數據中的一小部分樣本幾乎決定了PC。
你應該注意這樣的情況,并驗證降維方法捕獲的結構是否能代表大部分數據,而不僅僅是少數異常值。在降維圖中,異常值是遠離大多數觀測值的點。在PCA和其他線性方法中,如果樣本投影圖中的所有點都位于原點即圖的中心附近,只有一兩個點位于很遠的地方,降維結果將被異常值控制。應該使用特定數據質量控制指標對這些點進行檢驗,并考慮將其刪除。
如果刪除了樣本,則需要重新進行降維計算,并且應注意輸出表示中的更改。通過比較去除異常值前后的降維可視化,觀察觀察點的變化。你不僅應該考慮刪除異常值,還應該考慮刪除異常組,即與多數數據有很大不同的異常類。除去異常組并重新進行降維計算,得到適合大部分數據的模式。另一方面,如果數據集中包含許多異常觀測,則應使用穩定的方法,比如健壯的核主成分分析。
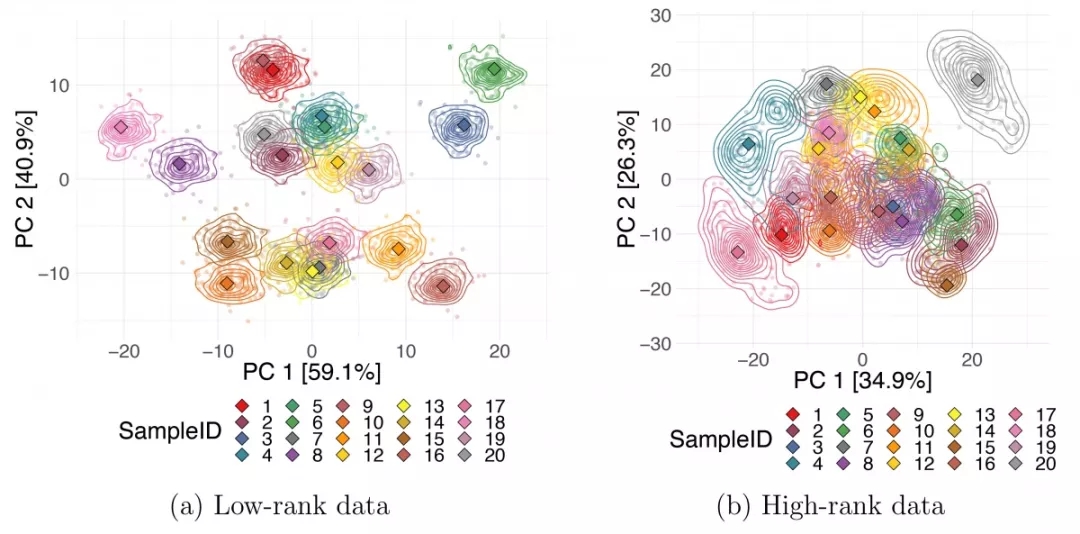
此外,可以通過構建“引導”數據集來估計與觀察點相關的不確定性,即用替換方法重采樣觀察點以生成數據的隨機子集。“引導”集可以看作是多路數據,使用技巧8中描述的STATIS或Procrustes對齊方法匹配隨機子集。當數據的真實噪聲模型可用時,可以生成數據點的副本,而不需要使用自舉子樣本。通過擾動樣本的測量值,并應用技巧9中提到的STATIS或DiSTATIS方法生成“折中方案”和每個受干擾的數據副本的坐標。獲取每個數據點的多個估計值后就可以估計它的不確定性。你可以使用密度等值線或通過將每個引導程序投影中的所有數據點繪制到折中方案上來顯示DR嵌入圖上每個樣本的不確定性。圖9表示兩個模擬數據集的PCA投影的Procrustes比對。彩色線表示自舉子集輸出坐標的密度等值線,菱形標記對應于全部數據的投影坐標。圖中繪制了20個合成數據點,這些數據點分別來自2維高斯分布和5維高斯分布,均正交投影到10維。我們可以觀察到低秩數據點的不確定性要小得多,即前2個PC能更好地代表***個數據集。
圖9.數據點的不確定性
每個數據點的降維輸出坐標的穩定性。 使用Procrustes變換將兩個10維模擬數據集的bootstrap樣本投影到前兩個PC對齊,其中(a)中數據秩為2、(b)中數據秩為5。 較小的圓形標記對應于每個bootstrap試驗,較大的菱形標記是整個數據集的坐標。DR,dimensionality reduction,即降維;PC,principal component,即主成分。
結語
在分析高維數據時,降維非常有用,有時甚至是必不可少的。盡管降維方法被廣泛采用,但經常被誤用或誤解。現有方法的降維方法五花八門,更不用說其中一些方法還有著各種不同的相異度指標和參數設置。這十項技巧可以為從業者提供一個檢查表或作為一個非正式的指南。我們描述了執行有效降維的一般步驟,并給出了正確解釋和充分理解降維算法輸出的方法。這里討論的大部分建議都適用于所有降維方法,但部分建議是針對特定降維方法的。
除了上述內容,我們還想提供一條額外的建議:跟蹤你所做出的的所有決策,包括選擇的方法、選擇的距離或內核以及使用的參數值。R、IPython和Jupyter notebook允許生成包含敘述文本、代碼及其輸出的完整分析報告,是保存所有步驟以及獲得結果方便的方法。記錄你的選擇是可重復研究的關鍵部分;它允許其他人復制你所獲得的結果,并在你下次處理類似數據時加快分析過程。我們提供了在S1 Text文本中使用R-markdown生成的可重現報告的示例和其代碼文件。
相關報道:
https://journals.plos.org/ploscompbiol/article id=10.1371/journal.pcbi.1006907
【本文是51CTO專欄機構大數據文摘的原創文章,微信公眾號“大數據文摘( id: BigDataDigest)”】