在新數據中，深度學習系統執行(泛化)能力如何?其性能如何?要想建立AI系統的信賴度和可靠性，必須估計算法的泛化能力。

[[272740]]

我們能信任AI嗎?AI是否會像人類酗酒一樣毫無顧忌?一但AI啟動，是否會毀滅世界?

統計學習理論意義何在?

AI系統必須安全可靠，一旦啟動AI，算法才能按預期執行。確保AI算法性能良好是提高其采用度和信任度的必由之路 [5]。

此外，決策人在歐盟委員會發布的《可信賴AI的倫理準則》(《ETHICS GUIDELINES FOR TRUSTWORTHY AI》)中明確規定要了解算法的泛化能力。

然而，模型泛化性(泛化理論)研究領域依然投資不足。目前唯一可繼續且可行的標準方法是進行數據拆分、驗證集和測試集。然而，盡管在無法量化算法的泛化能力時，在測試(留出)集上進行估計不失明智;但這一過程非常棘手，可能發生數據泄漏的風險，需要另外進行獨立性假設(獨立性驗證的參數單獨從留出集中選出)，但會與p-hacking 等實踐所混淆[20]。

什幺是泛化?

數據是由潛在的未知分布D生成的，這是上述工作的關鍵性假設。統計學習并非直接訪問分布，而是假定給出了訓練樣本S，其中S的每個元素均由D生成，并呈獨立同分布。學習算法從函數空間(假設類)H中選擇函數(假設h)，其中H = {f(x，α)}，α是參數向量。

于是，假設h的泛化誤差可定義為：從分布D中選取的樣本x的預期誤差與經驗損失(給定樣本S上的損失)之間的差值 [4,11]。

我們的任務是給泛化錯誤設定上限，看究竟會出現多幺嚴重的泛化錯誤。

傳統方法：模型能力

傳統泛化理論中，根據假設類H的復雜度(容量)建立泛化能力模型。簡單來說，類的“容量”取決于可以在這個類上擬合良好的數據集的數量。類的容量越大，這個類就越靈活，但也越容易過度擬合。[..]容量控制使用的是更加靈活的模型，以獲得良好擬合，那些非常靈活但過度擬合的模型則棄之不用[8]。

如何界定假設類H的復雜性?傳統泛化理論概念包括VC維、Rademacher復雜度和PAC-Bayes邊界。

VC維和死亡神經元

VC(Vapnik-Chervonenkis)維是一種通過評估函數彎曲程度來衡量函數類的復雜度的一種方式，H類的VC維即可以被H打散的最大樣本點數目。如果一組樣本點都能被函數打散，無論為一組內所有樣本點分配什幺樣的二進制標簽，該類樣本都可以將其完美分離。[5] 

Zhang等人的實驗[7]表明，在現實數據中訓練的深網真實的“參數復雜度”目前無人知曉，20多年前巴特利特(Bartlett)的VC計算(#節點數*#層)只是一個粗略設定的上限[ 2]。

死亡神經元的實驗數據表明，當網絡足夠大，并使用非線性激活函數ReLU時，許多權重為零[13]，這一點可能不足為奇。

那幺如何估計模型的VC維呢?

PAC可學習性和Rademacher復雜度

PAC(可能近似正確)可學習性的定義很簡單，即存在一種算法，對于每個分布D和Є，δ> 0，找到具有概率1-δ的“Є-最優”假設。每個分布都有一個算法的呼聲十分強烈，即Rademacher復雜度反而針對特定但未知的分布D而定義。

基于[23]的Rademacher復雜度的草圖推導

簡而言之，Rademacher復雜度衡量假設類H的能力，以適應隨機±1二進制標簽。與VC維相比，Rademacher復雜度取決于分布，可用于任何類別的實值函數(不僅是離散值函數)。

正如Bartlett的VC維計算，Rademacher復雜度缺乏有效的深度學習泛化界限。事實上，實驗測試表明，許多神經網絡用任意標簽完美擬合訓練集，于是，我們也希望相應模型H的Rademacher復雜度臻于完美。當然，這只是Rademacher復雜度的一個微不足道的上限，在現實環境中得不到有用的泛化界限[7]。

換句話說，理論研究尚未取得有效成果，只能從“煉金術”或一些最佳實踐中尋找解決辦法。有實踐表明：對Rademacher這種復雜學習架構來說，能夠真正降低其復雜度的唯一方法是使用訓練分類器，并通過留出集檢測缺少的泛化。世界上每一位從業者其實無意中已經做到了這一點。張等人的研究([7])得出的結論目前在該領域無人超越，獲得了認同。

新方法

當今機器學習模型相對復雜，很難用經典的泛化理論進行計算，更不能指導學習系統設計[2]。泛化理論的經典方法只是描述性的，換句話說，如果沒有發生泛化，可以通過利用復雜性度量(VC維和Rademacher)進行證明，但沒有任何可以規范性原則可以指導實踐[ 2]。

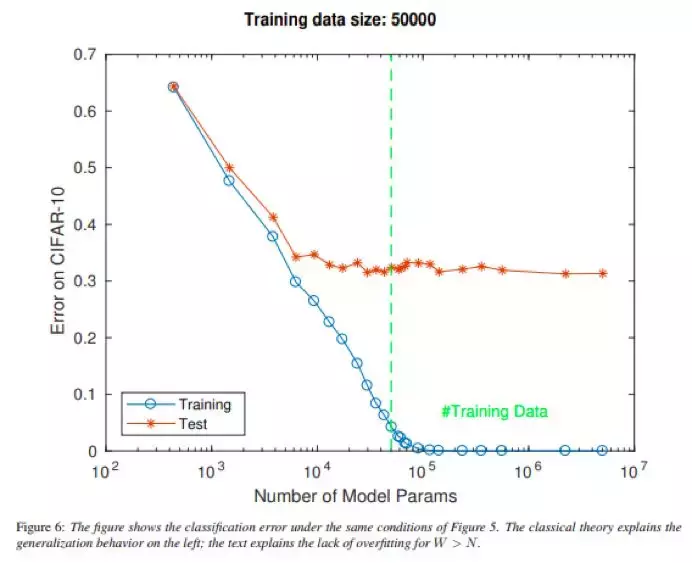
此外，實驗測試表明，容量接近于無限的假設類可能在實踐中運作良好。這不僅適用于深度學習模型，也適用于其他機器學習方法，例如一些帶有內核的支持向量機SVM(例如：徑向基函數)具有無限的VC維。更簡單的線性模型甚至可以欺騙我們，過度參數化線性模型的假設空間可以記憶任何訓練數據，并且隨著參數的范數任意變大，即使參數任意遠離真值參數[12]，該空間也可減少任意接近零(包括零)的訓練和測試誤差，深度學習極為重視傳統的泛化理論方法，哪怕過度參數化很高，或者容量較大(隨機標記的數據為零訓練誤差)[1]，深度網絡的一個主要難題還是在于缺少過度擬合。

目前，人們正重新審視復雜度的總體思路。關于深度學習，也出現了許多新穎的泛化方法。

基于范數的容量度量

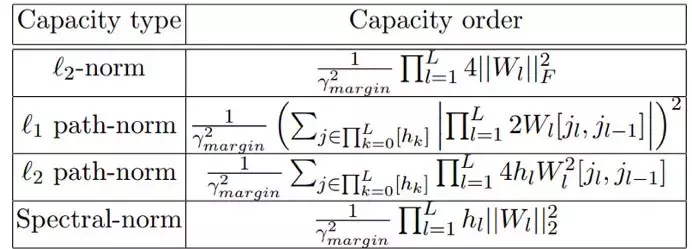
計算容量度量的途徑之一是由間距歸一化的權值矩陣的范數度量來查看容量度量。數據樣本的輸出分類間距是模型分配給正確類別的值減去所有其他類別的最大值的差異。 

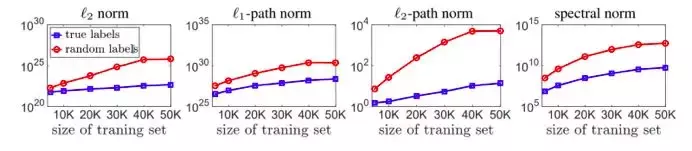
基于范數的測量并不完全依賴模型中的參數數量，因此可能能夠更好地表示其容量 的潛力[14]。基于范數的度量可以解釋深度神經網絡(DNN)的泛化，因為就復雜度而言，在隨機標簽上訓練的模型總是高于在真實標簽上訓練的模型，由此后者的泛化能力更加有利[14]。 

上圖表明這些測量可以解釋該泛化，因為隨機標簽學習模型的復雜度總是高于用真實標簽學習模型的復雜度。此外，隨著訓練集規模的增加[22]，二者復雜度之間的差距也在增加。

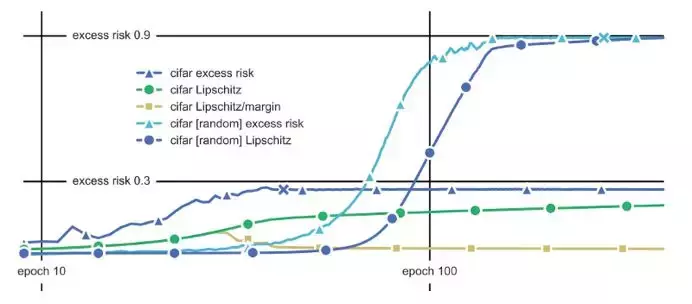
與之相關的另一個容量測量是網絡的利普希茨常數。利普希茨常數是權值矩陣的譜范數的乘積。譜范數是矩陣的最大奇異值：矩陣可以拉伸一個向量[9]。

利普希茨常數與超額風險相關(測試誤差減去訓練誤差)。然而，盡管風險過高，但這一度量隨著時間的推移而增長[4];其增長可以通過利普希茨常數的間距抵消掉，重復抵消可使增長歸一化(見圖4)。

壓縮方法

泛化的基本定理表明，如果訓練集具有m個樣本，那幺定義為訓練數據和測試數據誤差間差異的泛化誤差是sqrt(N’/ m)的量級，其中N’是網絡有效參數的數量 [或復雜度度量] [23,24]。

采用具有N個可訓練參數的矩陣C，并嘗試將其壓縮為另一個具有較少參數(N”)的C’和與C大致相同的訓練誤差。根據泛化基本定理，只要訓練樣本的數量超過N”，那幺C’(壓縮網!)就能進行良好的泛化[23,24]。

壓縮方法非常具有吸引力。一方面，可以確定DNN的泛化界限。另一方面，能夠獲得廣泛的實踐和運營優勢：

1. 在生產中使用相對較小(的訓練)模型有許多好處，運算速度更快，耗能更低(這一點在移動和嵌入式應用中很重要)，并且消耗更少的內存。
2. 最近的研究提出了“彩票假設”的經驗證據，隨機初始化的密集神經網絡包含一個子網絡(中獎彩票)，該子網被初始化，以便隔離訓練。經過訓練的子網可以匹配原始網絡的測試精度，最多實現相同的迭代次數[16]。采用能夠識別獲獎門票的訓練策略轉化為a)更快學習b)更高的測試準確度和c)…;)

除了“彩票票據方法”之外，還有很多其他有趣的網絡壓縮方法。其中一個非常有吸引力的想法受到了TensorNetworks的啟發：“Tensor Train”的概念顯示了DNN全連接層的權值矩陣，顯示出已經很有希望的實證結果[17]。

盡管這種壓縮通常需要重新訓練壓縮網絡，但[25]提供了對網絡壓縮方法的調查，這是基于[23,24]提供的基本定理和壓縮的泛化理論的方法所沒有考慮到的地方。

結論

為了保證深度學習算法的可靠性，必須得出有效的(緊密的)泛化界限。對這一問題，傳統方法(VC維、Rademacher)未能給出答案，而新的方法尚待研究。