海量樣本無(wú)從下手?五種抽樣算法分分鐘搞定
數(shù)據(jù)科學(xué)是研究算法的學(xué)科。本文介紹了一些常見的用于處理數(shù)據(jù)的抽樣技術(shù)。
1. 簡(jiǎn)單隨機(jī)抽樣
假設(shè)要從一個(gè)群體中選出一個(gè)集合,該集合中的每個(gè)成員選中的概率相等。
下列代碼演示了如何從數(shù)據(jù)集中選擇100個(gè)采樣點(diǎn)。
- sample_df = df.sample(100)
2. 分層抽樣
假設(shè)需要估計(jì)選舉中每個(gè)候選人的平均票數(shù)。并且假設(shè)該國(guó)有3個(gè)城鎮(zhèn):
A鎮(zhèn)有100萬(wàn)名工人,B鎮(zhèn)有200萬(wàn)名工人,C鎮(zhèn)有300萬(wàn)名退休人員。
在所有選民中抽取60個(gè)隨機(jī)樣本,但隨機(jī)樣本有可能不能很好地與這些城鎮(zhèn)的特征相適應(yīng),因此會(huì)產(chǎn)生數(shù)據(jù)偏差,從而導(dǎo)致估算結(jié)果出現(xiàn)重大錯(cuò)誤。
相反,如果分別從A,B和C鎮(zhèn)抽取10,20和30個(gè)隨機(jī)樣本,那么,在相同的樣本數(shù)的情況下,用該種方法估算的結(jié)果誤差較小。
使用python可以很容易地做到這一點(diǎn):
- from sklearn.model_selection import train_test_split
- X_train, X_test, y_train, y_test = train_test_split(X, y,
- stratify=y,
- test_size=0.25)
3. 水塘抽樣
假設(shè)有未知數(shù)量的大項(xiàng)目流,并且只供迭代一次。數(shù)據(jù)科學(xué)家可以創(chuàng)建一個(gè)算法,從項(xiàng)目流中隨機(jī)選擇一個(gè)項(xiàng)目以使每個(gè)項(xiàng)目抽中的概率相等。如何實(shí)現(xiàn)這一步驟?
假設(shè)必須從無(wú)限大的項(xiàng)目流中抽取5個(gè)對(duì)象,這樣每個(gè)對(duì)象被抽中的概率都相等。
- import randomdef generator(max):
- number = 1
- while number < max:
- number += 1
- yield number
- # Create as stream generator
- stream = generator(10000)
- # Doing Reservoir Sampling from the stream
- k=5
- reservoir = []
- for i, element in enumerate(stream):
- if i+1<= k:
- reservoir.append(element)
- else:
- probability = k/(i+1)
- if random.random() < probability:
- # Select item in stream and remove one of the k items already selected
- reservoir[random.choice(range(0,k))] = element
- print(reservoir)
- ------------------------------------
- [1369, 4108, 9986, 828, 5589]
從數(shù)學(xué)上可以證明,在樣本中,每個(gè)元素從項(xiàng)目流中被抽中的概率相等。
怎么做呢?
涉及到數(shù)學(xué)時(shí),從小的問題著手總是有用的。
所以,假設(shè)要從一個(gè)只有3個(gè)項(xiàng)目的數(shù)據(jù)流中抽出其中2個(gè)。
由于水塘空間充足,可將項(xiàng)目1放入列表,同理,由于水塘空間仍然充足,可將項(xiàng)目2也放入列表。
再看項(xiàng)目3。事情就變得有趣了,項(xiàng)目3被抽中的概率為2/3.
現(xiàn)在來(lái)看看項(xiàng)目1被抽中的概率:
項(xiàng)目1被抽中的概率等于項(xiàng)目3被抽中的概率乘以項(xiàng)目1被隨機(jī)選為數(shù)據(jù)流中其他兩個(gè)項(xiàng)目的候補(bǔ)的概率,即:
- 2/3*1/2 = 1/3
因此,抽中項(xiàng)目1的概率為:
- 1–1/3 = 2/3
數(shù)據(jù)科學(xué)家可以對(duì)項(xiàng)目2使用完全相同的參數(shù),并且將該參數(shù)運(yùn)用于數(shù)據(jù)流中的其他更多項(xiàng)目。
因此,每個(gè)項(xiàng)目被抽中的概率相同:2/3或一般式k/n
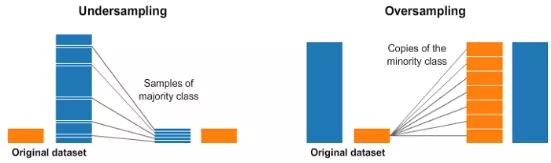
4. 隨機(jī)欠采樣和過采樣
事實(shí)上,不均衡數(shù)據(jù)集十分常見。
重抽樣是一種廣泛用于處理極度不均衡數(shù)據(jù)集的技術(shù)。它指從多數(shù)類樣本中排除部分樣本(欠采樣)和/或從少數(shù)類樣本中添加更多樣本(過采樣)。
首先,創(chuàng)建一些不均衡數(shù)據(jù)的示例。
- from sklearn.datasets import make_classification
- X, y = make_classification(
- n_classes=2, class_sep=1.5, weights=[0.9, 0.1],
- n_informative=3, n_redundant=1, flip_y=0,
- n_features=20, n_clusters_per_class=1,
- n_samples=100, random_state=10
- )
- X = pd.DataFrame(X)
- X['target'] = y
現(xiàn)可以使用以下方法進(jìn)行隨機(jī)過采樣和欠采樣:
- num_0 = len(X[X['target']==0])
- num_1 = len(X[X['target']==1])
- print(num_0,num_1)
- # random undersample
- undersampled_data = pd.concat([ X[X['target']==0].sample(num_1) , X[X['target']==1] ])
- print(len(undersampled_data))
- # random oversample
- oversampled_data = pd.concat([ X[X['target']==0] , X[X['target']==1].sample(num_0, replace=True) ])
- print(len(oversampled_data))
- ------------------------------------------------------------
- OUTPUT:
- 90 10
- 20
- 180
5. 使用Imbalanced-learn進(jìn)行欠采樣和過采樣
Imbalanced-learn(imblearn)是一個(gè)解決不均衡數(shù)據(jù)集的Python語(yǔ)言包。
可提供多種方法進(jìn)行欠采樣和過采樣。
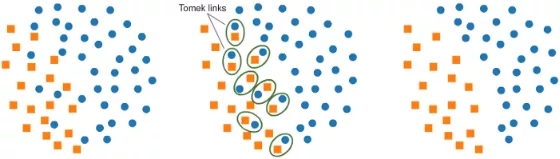
(1) 使用Tomek Links進(jìn)行欠采樣:
Imbalanced-learn提供的方法之一是Tomek Links,指的是在兩個(gè)不同類的樣本中最近鄰的對(duì)方。
在這個(gè)算法中,最終要將多數(shù)類樣本從Tomek Links中移除,這為分類器提供了一個(gè)更好的決策邊界。
- from imblearn.under_sampling import TomekLinks
- tl = TomekLinks(return_indices=True, ratio='majority')
- X_tl, y_tl, id_tl = tl.fit_sample(X, y)
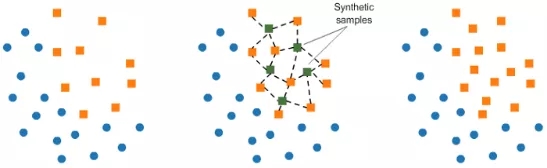
(2) 使用SMOTE算法進(jìn)行過采樣
SMOTE算法(合成少數(shù)類過采樣技術(shù)),即在已有的樣本最近鄰中,為少數(shù)類樣本人工合成新樣本。
- from imblearn.over_sampling import SMOTE
- smote = SMOTE(ratio='minority')
- X_sm, y_sm = smote.fit_sample(X, y)
Imblearn包中還有許多其他方法可用于欠采樣(Cluster Centroids,NearMiss等)和過采樣(ADASYN和bSMOTE)。
結(jié)語(yǔ)
算法是數(shù)據(jù)科學(xué)的生命線。
抽樣是數(shù)據(jù)科學(xué)中的一個(gè)重要課題。一個(gè)好的抽樣策略有時(shí)可以推動(dòng)整個(gè)項(xiàng)目發(fā)展。而錯(cuò)誤的抽樣策略可能會(huì)帶來(lái)錯(cuò)誤的結(jié)果。因此,應(yīng)當(dāng)謹(jǐn)慎選擇抽樣策略。