前言

Matplotlib是一個流行的Python庫，可以很容易地用于創(chuàng)建數(shù)據(jù)可視化。然而，設(shè)置數(shù)據(jù)、參數(shù)、圖形和繪圖在每次執(zhí)行新項目時都可能變得非常混亂和繁瑣。而且由于應(yīng)用不同，我們不知道選擇哪一個圖例，比如直方圖，餅狀圖，曲線圖等等。這里有一個很棒的思維導(dǎo)圖，可以幫助您為工作選擇正確的可視化效果：

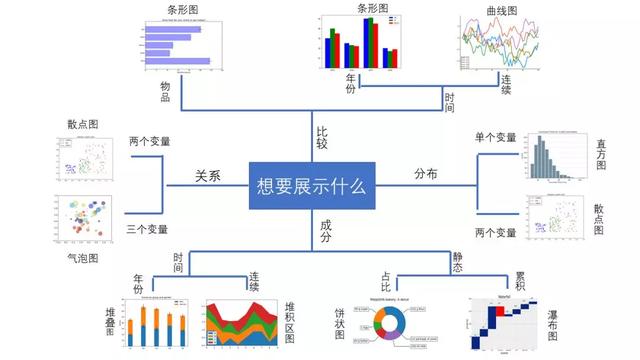
我們對于這張思維導(dǎo)圖中的主要圖例做一些解釋：

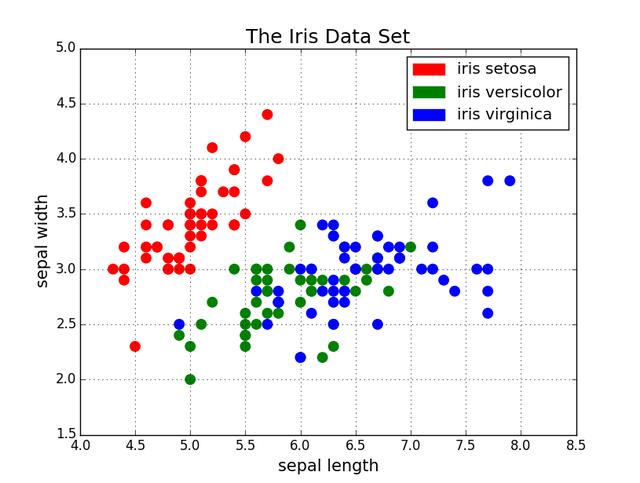
散點圖

散點圖非常適合顯示兩個變量之間的關(guān)系，因為您可以直接看到數(shù)據(jù)的原始分布。您還可以通過如下圖所示的對組進行顏色編碼來查看不同數(shù)據(jù)組的這種關(guān)系。

想要可視化三個變量之間的關(guān)系嗎?!完全沒有異議只需使用另一個參數(shù)(如點大小)對第三個變量進行編碼，如下面的第二個圖所示，我們把這個圖叫做冒泡圖。

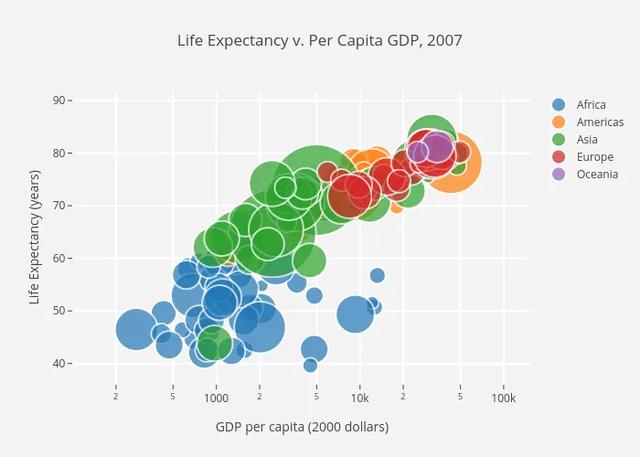
散點圖函數(shù)舉例：

scatter(x_data,y_data,s=10,color=color,alpha=0.75) 

線圖

當(dāng)你能清楚地看到一個變量與另一個變量之間變化很大時，最好使用線圖。讓我們看看下面的圖來說明。我們可以清楚地看到，所有專業(yè)的百分比隨時間變化很大。用散點圖來繪制這些圖會非常雜亂，很難真正理解和看到發(fā)生了什么。直線圖非常適合這種情況，因為它基本上可以快速總結(jié)兩個變量(百分比和時間)的協(xié)方差。同樣，我們也可以通過顏色編碼來使用分組。

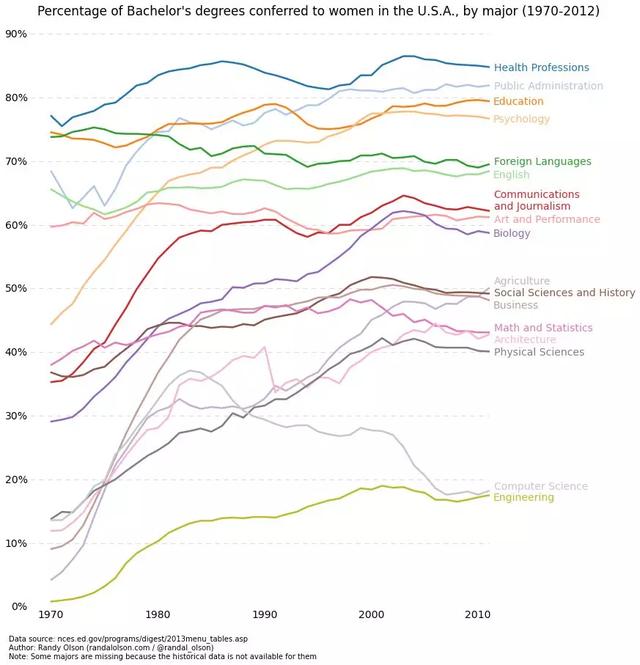
線圖代碼舉例：

plot(x_data, y_data, lw = 2, color = '#539caf', alpha = 1) 

直方圖

直方圖對于查看(或真正發(fā)現(xiàn))數(shù)據(jù)點的分布很有用。看看下面的柱狀圖，我們繪制了頻率和智商的柱狀圖。我們可以清楚地看到向中心的濃度和中值是什么。我們也可以看到它遵循一個高斯分布。使用條形圖(而不是散點圖)可以讓我們清楚地看到每個箱子頻率之間的相對差異。使用箱子(離散化)真的幫助我們看到“更大的畫面”，如果我們使用所有沒有離散箱子的數(shù)據(jù)點，在可視化中可能會有很多噪音，使我們很難看到到底發(fā)生了什么。

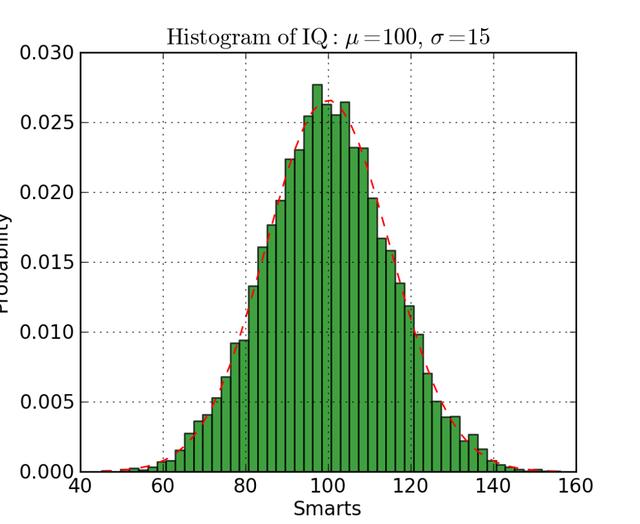
假設(shè)我們要比較數(shù)據(jù)中兩個變量的分布。有人可能會認(rèn)為，你必須制作兩個獨立的直方圖，把它們放在一起比較。但是，實際上有一個更好的方法:我們可以用不同的透明度覆蓋直方圖。看看下面的圖。均勻分布的透明度設(shè)為0。5這樣我們就能看到它的背后。這允許使用直接查看同一圖上的兩個分布。

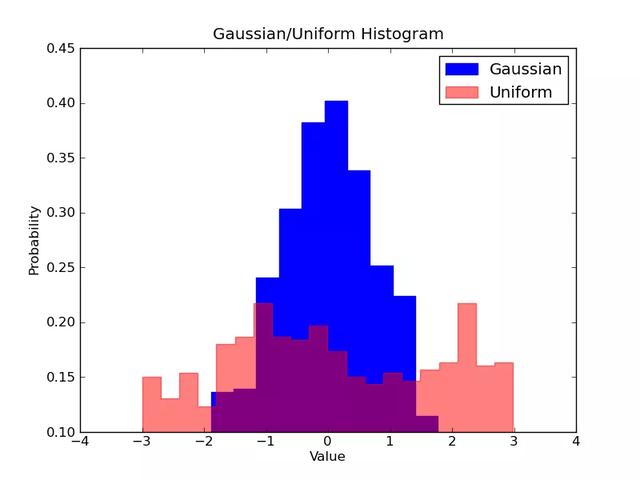
直方圖代碼舉例：

hist(data, n_bins = n_bins, cumulative = cumulative, color = '#539caf') 

條形圖

當(dāng)您試圖將類別很少(可能少于10個)的分類數(shù)據(jù)可視化時，條形圖是最有效的。如果我們有太多的類別，那么圖中的條形圖就會非常混亂，很難理解。它們非常適合分類數(shù)據(jù)，因為您可以根據(jù)條形圖的大小;分類也很容易劃分和顏色編碼。我們將看到三種不同類型的條形圖:常規(guī)的、分組的和堆疊的：

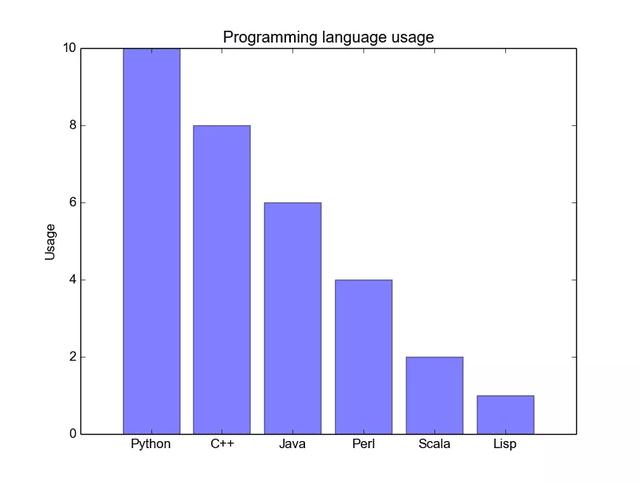
常規(guī)的條形圖代碼舉例：

bar(x_data, y_data, color = '#539caf', align = 'center') 

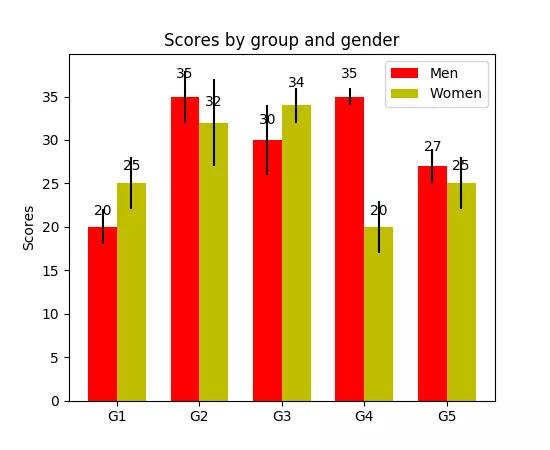
分組圖代碼舉例：

foriinrange(0,len(y_data_list)):    if i == 0:        bar(x_data,y_data_list[i],color=colors[i],align='center',label=y_data_names[i])else:  bar(x_data,y_data_list[i],color=colors[i],bottom=y_data_list[i-1],align='center',label=y_data_names[i]) 

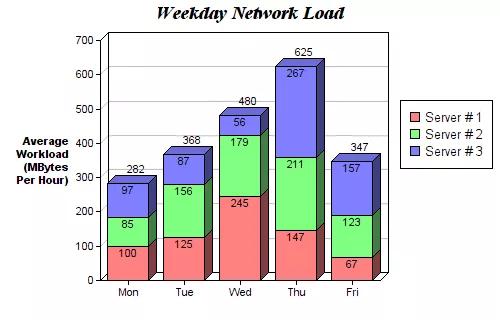
堆疊圖代碼舉例：

for i in range(0, len(y_data_list)):bar(x_data+alteration[i],y_data_list[i],color=colors[i],label=y_data_names[i],width=ind_width)