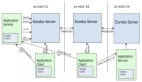
與程序員相關的CPU緩存知識
好久沒有寫一些微觀方面的文章了,今天寫一篇關于 CPU Cache 相關的文章,這篇文章比較長,主要分成這么幾個部分:基礎知識、緩存的命中、緩存的一致性、相關的代碼示例和延伸閱讀。其中會講述一些多核 CPU 的系統架構以及其原理,包括對程序性能上的影響,以及在進行并發編程的時候需要注意到的一些問題。這篇文章我會盡量地寫簡單和通俗易懂一些,主要是講清楚相關的原理和問題,而對于一些細節和延伸閱讀我會在文章最后會給出相關的資源。
因為無論你寫什么樣的代碼都會交給 CPU 來執行,所以,如果你想寫出性能比較高的代碼,這篇文章中提到的技術還是值得認真學習的。
基礎知識
首先,我們都知道現在的 CPU 多核技術,都會有幾級緩存,老的 CPU 會有兩級內存(L1 和 L2),新的 CPU 會有三級內存(L1,L2,L3 ),如下圖所示:
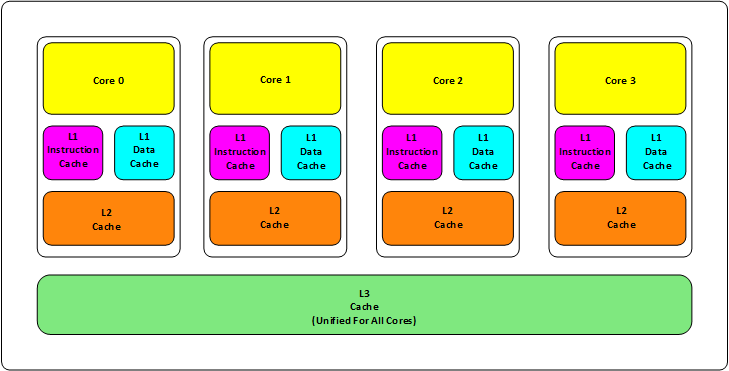
其中:
- L1 緩分成兩種,一種是指令緩存,一種是數據緩存。L2 緩存和 L3 緩存不分指令和數據。
- L1 和 L2 緩存在第一個 CPU 核中,L3 則是所有 CPU 核心共享的內存。
- L1、L2、L3 的越離 CPU 近就越小,速度也越快,越離 CPU 遠,速度也越慢。
再往后面就是內存,內存的后面就是硬盤。我們來看一些他們的速度:
- L1 的存取速度:4 個 CPU 時鐘周期
- L2 的存取速度: 11 個 CPU 時鐘周期
- L3 的存取速度:39 個 CPU 時鐘周期
- RAM 內存的存取速度:107 個 CPU 時鐘周期
我們可以看到,L1 的速度是 RAM 的 27 倍,但是 L1/L2 的大小基本上也就是 KB 級別的,L3 會是 MB 級別的。例如:Intel Core i7-8700K ,是一個 6 核的 CPU,每核上的 L1 是 64KB(數據和指令各 32KB),L2 是 256K,L3 有 12MB(我的蘋果電腦是 Intel Core i9-8950HK,和 Core i7-8700K 的 Cache 大小一樣)。
我們的數據就從內存向上,先到 L3,再到 L2,再到 L1,最后到寄存器進行 CPU 計算。為什么會設計成三層?這里有下面幾個方面的考慮:
- 一個方面是物理速度,如果要更大的容量就需要更多的晶體管,除了芯片的體積會變大,更重要的是大量的晶體管會導致速度下降,因為訪問速度和要訪問的晶體管所在的位置成反比,也就是當信號路徑變長時,通信速度會變慢。這部分是物理問題。
- 另外一個問題是,多核技術中,數據的狀態需要在多個 CPU 中進行同步,并且,我們可以看到,cache 和 RAM 的速度差距太大,所以,多級不同尺寸的緩存有利于提高整體的性能。
這個世界永遠是平衡的,一面變得有多光鮮,另一面也會變得有多黑暗。建立這么多級的緩存,一定就會引入其它的問題,這里有兩個比較重要的問題,
- 一個是比較簡單的緩存的命中率的問題。
- 另一個是比較復雜的緩存更新的一致性問題。
尤其是第二個問題,在多核技術下,這就很像分布式的系統了,要對多個地方進行更新。
緩存的命中
在說明這兩個問題之前。我們需要要解一個術語 Cache Line。緩存基本上來說就是把后面的數據加載到離自己近的地方,對于 CPU 來說,它是不會一個字節一個字節的加載的,因為這非常沒有效率,一般來說都是要一塊一塊的加載的,對于這樣的一塊一塊的數據單位,術語叫“Cache Line”,一般來說,一個主流的 CPU 的 Cache Line 是 64 Bytes(也有的 CPU 用 32Bytes 和 128Bytes),64Bytes 也就是 16 個 32 位的整型,這就是 CPU 從內存中撈數據上來的最小數據單位。
比如:Cache Line 是最小單位(64Bytes),所以先把 Cache 分布多個 Cache Line,比如:L1 有 32KB,那么,32KB/64B = 512 個 Cache Line。
一方面,緩存需要把內存里的數據放到放進來,英文叫 CPU Associativity。Cache 的數據放置的策略決定了內存中的數據塊會拷貝到 CPU Cache 中的哪個位置上,因為 Cache 的大小遠遠小于內存,所以,需要有一種地址關聯的算法,能夠讓內存中的數據可以被映射到 Cache 中來。這個有點像內存地址從邏輯地址向虛擬地址映射的方法,但不完全一樣。
基本上來說,我們會有如下的一些方法。
- 一種方法是,任何一個內存地址的數據可以被緩存在任何一個 Cache Line 里,這種方法是最靈活的,但是,如果我們要知道一個內存是否存在于 Cache 中,我們就需要進行O(n)復雜度的 Cache 遍歷,這是很沒有效率的。
- 另一種方法,為了降低緩存搜索算法,我們需要使用像 Hash Table 這樣的數據結構,最簡單的 hash table 就是做“求模運算”,比如:我們的 L1 Cache 有 512 個 Cache Line,那么,公式:
(內存地址 mod 512)* 64就可以直接找到所在的 Cache 地址的偏移了。但是,這樣的方式需要我們的程序對內存地址的訪問要非常地平均,不然沖突就會非常嚴重。這成了一種非常理想的情況了。 - 為了避免上述的兩種方案的問題,于是就要容忍一定的 hash 沖突,也就出現了 N-Way 關聯。也就是把連續的N個 Cache Line 綁成一組,然后,先把找到相關的組,然后再在這個組內找到相關的 Cache Line。這叫 Set Associativity。如下圖所示。
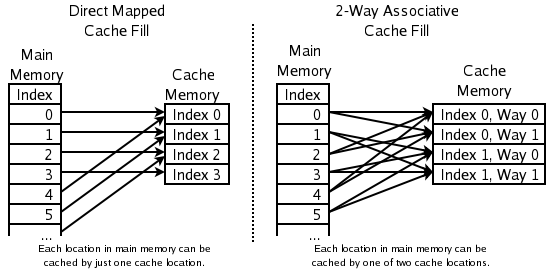
對于 N-Way 組關聯,可能有點不好理解,這里個例子,并多說一些細節(不然后面的代碼你會不能理解),Intel 大多數處理器的 L1 Cache 都是 32KB,8-Way 組相聯,Cache Line 是 64 Bytes。這意味著,
- 32KB 的可以分成,32KB / 64 = 512 條 Cache Line。
- 因為有 8 Way,于是會每一 Way 有 512 / 8 = 64 條 Cache Line。
- 于是每一路就有 64 x 64 = 4096 Byts 的內存。
為了方便索引內存地址,
- Tag:每條 Cache Line 前都會有一個獨立分配的 24 bits 來存的 tag,其就是內存地址的前 24bits
- Index:內存地址后續的 6 個 bits 則是在這一 Way 的是 Cache Line 索引,2^6 = 64 剛好可以索引 64 條 Cache Line
- Offset:再往后的 6bits 用于表示在 Cache Line 里的偏移量
如下圖所示:(更多的細節可以讀一下《Cache: a place for concealment and safekeeping》)
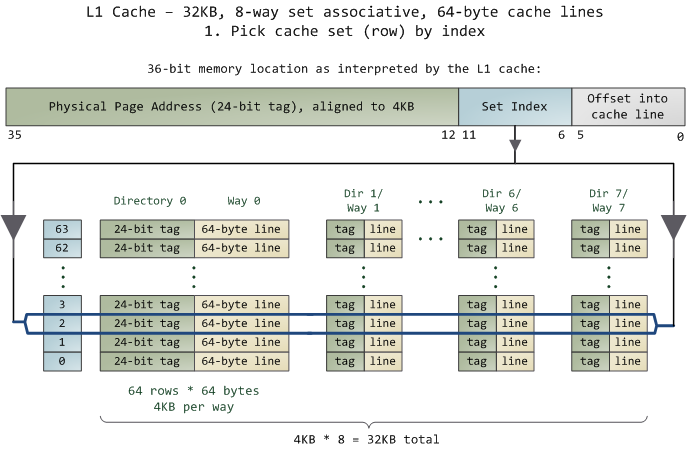
(圖片來自《Cache: a place for concealment and safekeeping》)
這也意味著:
- L1 Cache 可映射 36bits 的內存地址,一共 2^36 = 64GB 的內存
- 因為只要頭 24bits 相同就會被映射到同一個 Way 中,所以,基本上就是說,有2^12 = 4096 個地址會放在同一 Way 中。
- 當 CPU 要訪問一個內存的時候,通過這個內存的前 24bits 和中間的 6bits 可以直接定位相應的 Cache Line。
此外,當有數據沒有命中緩存的時候,CPU 就會以最小為 Cache Line 的單元向內存更新數據。當然,CPU 并不一定只是更新 64Bytes,因為訪問主存是在是太慢了,所以,一般都會多更新一些。好的 CPU 會有一些預測的技術,如果找到一種 pattern 的話,就會預先加載更多的內存,包括指令也可以預加載。這叫 Prefetching 技術 (參看,Wikipedia 的 Cache Prefetching 和 紐約州立大學的 Memory Prefetching)。比如,你在 for-loop 訪問一個連續的數組,你的步長是一個固定的數,內存就可以做到 prefetching。(注:指令也是以預加載的方式執行,參看本站的《代碼執行的效率》中的第三個示例)
了解這些細節,會有利于我們知道在什么情況下有可以導致緩存的失效。
緩存的一致性
對于主流的 CPU 來說,緩存的寫操作基本上是兩種策略(參看本站《緩存更新的套路》),
- 一種是 Write Back,寫操作只要在 cache 上,然后再 flush 到內存上。
- 一種是 Write Through,寫操作同時寫到 cache 和內存上。
為了提高寫的性能,一般來說,主流的 CPU(如:Intel Core i7/i9)采用的是 Write Back 的策略,因為直接寫內存實在是太慢了。
好了,現在問題來了,如果有一個數據 x 在 CPU 第 0 核的緩存上被更新了,那么其它 CPU 核上對于這個數據 x 的值也要被更新,這就是緩存一致性的問題。(當然,對于我們上層的程序我們不用關心 CPU 多個核的緩存是怎么同步的,這對上層的代碼來說都是透明的)
一般來說,在 CPU 硬件上,會有兩種方法來解決這個問題。
- Directory 協議。這種方法的典型實現是要設計一個集中式控制器,它是主存儲器控制器的一部分。其中有一個目錄存儲在主存儲器中,其中包含有關各種本地緩存內容的全局狀態信息。當單個 CPU Cache 發出讀寫請求時,這個集中式控制器會檢查并發出必要的命令,以在主存和 CPU Cache 之間或在 CPU Cache 自身之間進行數據同步和傳輸。
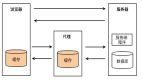
- Snoopy 協議。這種協議更像是一種數據通知的總線型的技術。CPU Cache 通過這個協議可以識別其它 Cache 上的數據狀態。如果有數據共享的話,可以通過廣播機制將共享數據的狀態通知給其它 CPU Cache。這個協議要求每個 CPU Cache 都可以“窺探”數據事件的通知并做出相應的反應。如下圖所示,有一個 Snoopy Bus 的總線。
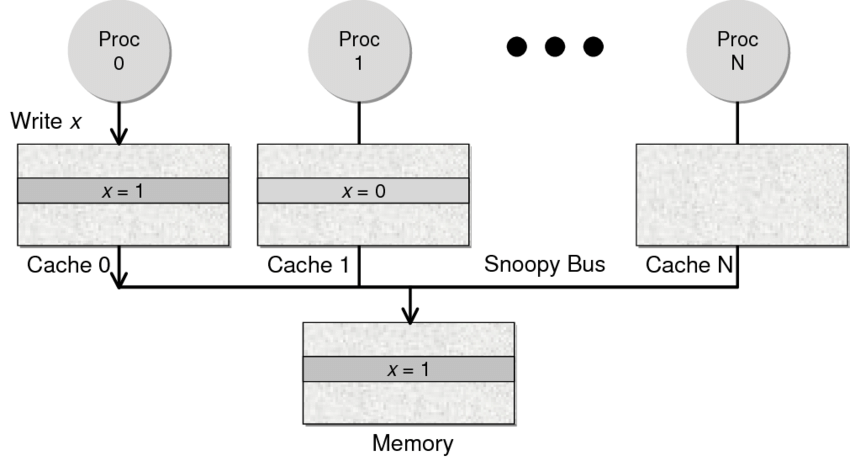
因為 Directory 協議是一個中心式的,會有性能瓶頸,而且會增加整體設計的復雜度。而 Snoopy 協議更像是微服務+消息通訊,所以,現在基本都是使用 Snoopy 的總線的設計。
這里,我想多寫一些細節,因為這種微觀的東西,不自然就就會更分布式系統相關聯,在分布式系統中我們一般用 Paxos/Raft 這樣的分布式一致性的算法。而在 CPU 的微觀世界里,則不必使用這樣的算法,原因是因為 CPU 的多個核的硬件不必考慮網絡會斷會延遲的問題。所以,CPU 的多核心緩存間的同步的核心就是要管理好數據的狀態就好了。
這里介紹幾個狀態協議,先從最簡單的開始,MESI 協議,這個協議跟那個著名的足球運動員梅西沒什么關系,其主要表示緩存數據有四個狀態:Modified(已修改), Exclusive(獨占的),Shared(共享的),Invalid(無效的)。
這些狀態的狀態機如下所示(有點復雜,你可以先不看,這個圖就是想告訴你狀態控制有多復雜):
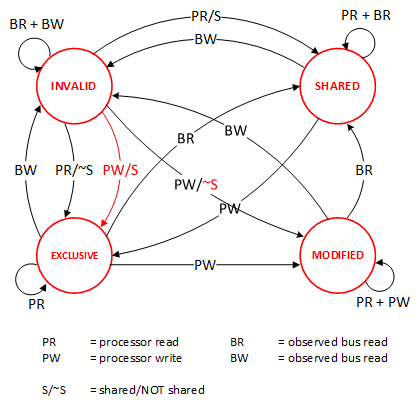
下面是個示例(如果你想看一下動畫演示的話,這里有一個網頁(MESI Interactive Animations),你可以進行交互操作,這個動畫演示中使用的 Write Through 算法):
| 當前操作 | CPU0 | CPU1 | Memory | 說明 |
|---|---|---|---|---|
| 1) CPU0 read (x) | x=1 (E) | x=1 | 只有一個 CPU 有 x 變量, 所以,狀態是 Exclusive |
|
| 2) CPU1 read (x) | x=1 (S) | x=1(S) | x=1 | 有兩個 CPU 都讀取 x 變量, 所以狀態變成 Shared |
| 3) CPU0 write (x,9) | x=9 (M) | x=1(I) | x=1 | 變量改變,在 CPU0 中狀態 變成 Modified,在 CPU1 中 狀態變成 Invalid |
| 4) 變量 x 寫回內存 | x=9 (M) | X=1(I) | x=9 | 目前的狀態不變 |
| 5) CPU1 read (x) | x=9 (S) | x=9(S) | x=9 | 變量同步到所有的 Cache 中, 狀態回到 Shared |
MESI 這種協議在數據更新后,會標記其它共享的 CPU 緩存的數據拷貝為 Invalid 狀態,然后當其它 CPU 再次 read 的時候,就會出現 cache miss 的問題,此時再從內存中更新數據。從內存中更新數據意味著 20 倍速度的降低。我們能不能直接從我隔壁的 CPU 緩存中更新?是的,這就可以增加很多速度了,但是狀態控制也就變麻煩了。還需要多來一個狀態:Owner (宿主),用于標記,我是更新數據的源。于是,現了 MOESI 協議
MOESI 協議的狀態機和演示示例我就不貼了,我們只需要理解 MOESI 協議允許 CPU Cache 間同步數據,于是也降低了對內存的操作,性能是非常大的提升,但是控制邏輯也非常復雜。
順便說一下,與 MOESI 協議類似的一個協議是 MESIF,其中的 F 是 Forward,同樣是把更新過的數據轉發給別的 CPU Cache 但是,MOESI 中的 Owner 狀態和 MESIF 中的 Forward 狀態有一個非常大的不一樣—— Owner 狀態下的數據是 dirty 的,還沒有寫回內存,Forward 狀態下的數據是 clean 的,可以丟棄而不用另行通知。
需要說明的是,AMD 用 MOESI,Intel 用 MESIF。所以,F 狀態主要是針對 CPU L3 Cache 設計的(前面我們說過,L3 是所有 CPU 核心共享的)。(相關的比較可以參看 StackOverlow 上這個問題的答案)
程序性能
了解了我們上面的這些東西后,我們來看一下對于程序的影響。
示例一
首先,假設我們有一個 64M 長的數組,設想一下下面的兩個循環:
- const int LEN = 64*1024*1024;
- int *arr = new int[LEN];
- for (int i = 0; i < LEN; i += 2) arr[i] *= i;
- for (int i = 0; i < LEN; i += 8) arr[i] *= i;
按我們的想法來看,第二個循環要比第一個循環少 4 倍的計算量,其應該也是要快 4 倍的。但實際跑下來并不是,在我的機器上,第一個循環需要 127 毫秒,第二個循環則需要 121 毫秒,相差無幾。這里最主要的原因就是 Cache Line,因為 CPU 會以一個 Cache Line 64Bytes 最小時單位加載,也就是 16 個 32bits 的整型,所以,無論你步長是 2 還是8,都差不多。而后面的乘法其實是不耗 CPU 時間的。
示例二
我們再來看一個與緩存命中率有關的代碼,我們以一定的步長increment 來訪問一個連續的數組。
- for (int i = 0; i < 10000000; i++) {
- for (int j = 0; j < size; j += increment) {
- memory[j] += j;
- }
- }
我們測試一下,在下表中, 表頭是步長,也就是每次跳多少個整數,而縱向是這個數組可以跳幾次(你可以理解為要幾條 Cache Line),于是表中的任何一項代表了這個數組有多少,而且步長是多少。比如:橫軸是 512,縱軸是4,意思是,這個數組有 4*512 = 2048 個長度,訪問時按 512 步長訪問,也就是訪問其中的這幾項:[0, 512, 1024, 1536] 這四項。
表中同的項是,是循環 1000 萬次的時間,單位是“微秒”(除以 1000 后是毫秒)
- | count | 1 | 16 | 512 | 1024 |
- ------------------------------------------
- | 1 | 17539 | 16726 | 15143 | 14477 |
- | 2 | 15420 | 14648 | 13552 | 13343 |
- | 3 | 14716 | 14463 | 15086 | 17509 |
- | 4 | 18976 | 18829 | 18961 | 21645 |
- | 5 | 23693 | 23436 | 74349 | 29796 |
- | 6 | 23264 | 23707 | 27005 | 44103 |
- | 7 | 28574 | 28979 | 33169 | 58759 |
- | 8 | 33155 | 34405 | 39339 | 65182 |
- | 9 | 37088 | 37788 | 49863 |156745 |
- | 10 | 41543 | 42103 | 58533 |215278 |
- | 11 | 47638 | 50329 | 66620 |335603 |
- | 12 | 49759 | 51228 | 75087 |305075 |
- | 13 | 53938 | 53924 | 77790 |366879 |
- | 14 | 58422 | 59565 | 90501 |466368 |
- | 15 | 62161 | 64129 | 90814 |525780 |
- | 16 | 67061 | 66663 | 98734 |440558 |
- | 17 | 71132 | 69753 |171203 |506631 |
- | 18 | 74102 | 73130 |293947 |550920 |
我們可以看到,從[9,1024] 以后,時間顯注上升。包括[17,512] 和 [18,512] 也顯注上升。這是因為,我機器的 L1 Cache 是 32KB, 8 Way 的,前面說過,8 Way 的一個組有 64 個 Cache Line,也就是 4096 個字節,而 1024 個整型正好是 4096 Bytes,所以,一旦過了 8 Way + 4096 Bytes 這個界,每個步長都無法命中 L1 Cache,每次都是 Cache Miss,所以,導致訪問時間一下子就上升了。而 [16, 512]也是一樣的,其中的幾步開始導致 L1 Cache 開始失效。
示例三
接下來,我們再來看個示例。下面是一個二維數組的兩種遍歷方式,一個逐行遍歷,一個是逐列遍歷,這兩種方式在理論上來說,尋址和計算量都是一樣的,執行時間應該也是一樣的。
- const int row = 1024;
- const int col = 512
- int matrix[row][col];
- //逐行遍歷
- int sum_row=0;
- for(int r=0; r<row; r++) {
- for(int c=0; c<col; c++){
- sum_row += matrix[r];
- }
- }
- //逐列遍歷
- int sum_col=0;
- for(int c=0; c<col; c++) {
- for(int r=0; r<row; r++){
- sum_col += matrix[r];
- }
- }
然而,并不是,在我的機器上,得到下面的結果。
- 逐行遍歷:0.081ms
- 逐列遍歷:1.069ms
執行時間有十幾倍的差距。其中的原因,就是逐列遍歷對于 CPU Cache 的運作方式并不友好,所以,付出巨大的代價。
示例四
接下來,我們來看一下多核下的性能問題,參看如下的代碼。兩個線程在操作一個數組的兩個不同的元素(無需加鎖),線程循環 1000 萬次,做加法操作。在下面的代碼中,我高亮了一行,就是p2指針,要么是p[1],或是 p[18],理論上來說,無論訪問哪兩個數組元素,都應該是一樣的執行時間。
- void fn (int* data) {
- for(int i = 0; i < 10*1024*1024; ++i)
- *data += rand ();
- }
- int p[32];
- int *p1 = &p[0];
- int *p2 = &p[1]; // int *p2 = &p[30];
- thread t1(fn, p1);
- thread t2(fn, p2);
然而,并不是,在我的機器上執行下來的結果是:
- 對于
p[0]和p[1]:560ms - 對于
p[0]和p[30]:104ms
這是因為 p[0] 和 p[1] 在同一條 Cache Line 上,而 p[0] 和 p[30] 則不可能在同一條 Cache Line 上 ,CPU 的緩沖最小的更新單位是 Cache Line,所以,這導致雖然兩個線程在寫不同的數據,但是因為這兩個數據在同一條 Cache Line 上,就會導致緩存需要不斷進在兩個 CPU 的 L1/L2 中進行同步,從而導致了 5 倍的時間差異。
示例五
接下來,我們再來看一下另外一段代碼:我們想統計一下一個數組中的奇數個數,但是這個數組太大了,我們希望可以用多線程來完成,這個統計。下面的代碼中,我們為每一個線程傳入一個 id ,然后通過這個 id 來完成對應數組段的統計任務。這樣可以加快整個處理速度。
- int total_size = 16 * 1024 * 1024; //數組長度
- int* test_data = new test_data[total_size]; //數組
- int nthread = 6; //線程數(因為我的機器是 6 核的)
- int result[nthread]; //收集結果的數組
- void thread_func (int id) {
- result[id] = 0;
- int chunk_size = total_size / nthread + 1;
- int start = id * chunk_size;
- int end = min (start + chunk_size, total_size);
- for ( int i = start; i < end; ++i ) {
- if (test_data[i] % 2 != 0 ) ++result[id];
- }
- }
然而,在執行過程中,你會發現,6 個線程居然跑不過 1 個線程。因為根據上面的例子你知道 result[] 這個數組中的數據在一個 Cache Line 中,所以,所有的線程都會對這個 Cache Line 進行寫操作,導致所有的線程都在不斷地重新同步 result[] 所在的 Cache Line,所以,導致 6 個線程還跑不過一個線程的結果。這叫 False Sharing。
優化也很簡單,使用一個線程內的變量。
- void thread_func (int id) {
- result[id] = 0;
- int chunk_size = total_size / nthread + 1;
- int start = id * chunk_size;
- int end = min (start + chunk_size, total_size);
- int c = 0; //使用臨時變量,沒有 cache line 的同步了
- for ( int i = start; i < end; ++i ) {
- if (test_data[i] % 2 != 0 ) ++c;
- }
- result[id] = c;
- }
我們把兩個程序分別在 1 到 32 個線程上跑一下,得出的結果畫一張圖如下所示:
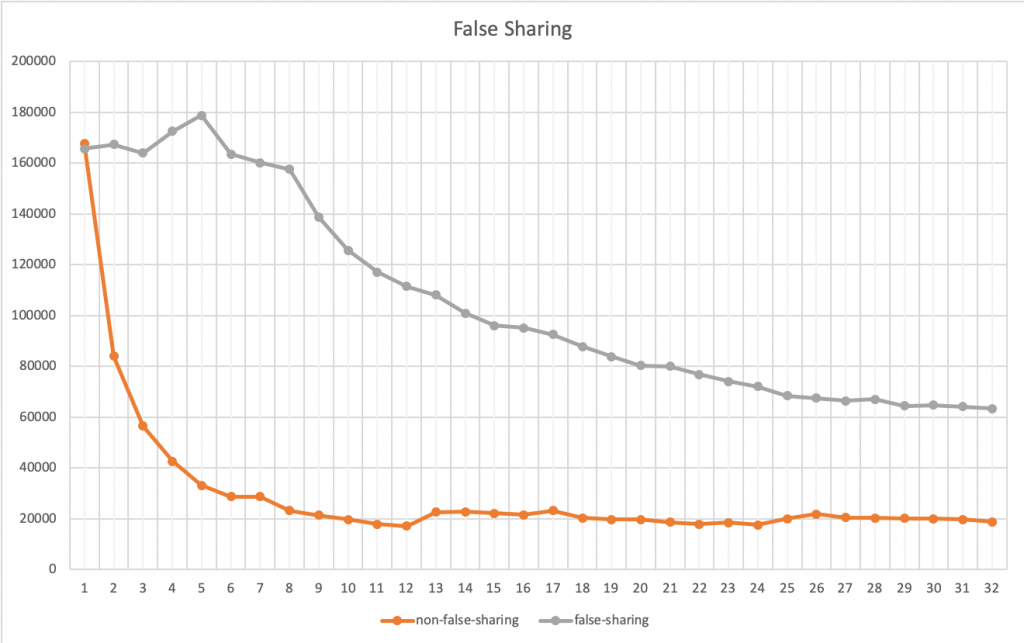
上圖中,我們可以看到,灰色的曲線就是第一種方法,橙色的就是第二種(用局部變量的)方法。當只有一個線程的時候,兩個方法相當,而且第二種方法還略差一點,但是在線程數增加的時候的時候,你會發現,第二種方法的性能提高的非常快。直到到達 6 個線程的時候,開始變得穩定(前面說過,我的 CPU 是 6 核的)。而第一種方法無論加多少線程也沒有辦法超過第二種方法。因為第一種方法不是 CPU Cache 友好的。
篇幅問題,示例就寫到這里,相關的代碼參看我的 Github 相關倉庫。