面試官提到的 AVL 樹,到底是個啥
了解過平衡二叉樹的朋友們,對它一定有印象,今天阿粉就與大家一起深入了解一下AVL樹!
一、摘要
在上篇文章,我們詳細的介紹了二叉樹的算法以及代碼實踐,我們知道不同的二叉樹形態結構,對查詢效率也會有很大的影響,尤其是當樹的形態結構變成一個鏈條結構的時候,查詢最后一個元素的效率極底,如何解決這個問題呢?
關鍵在于如何最大限度的減小樹的深度,從而提高查詢效率,正是基于這一點,平衡二叉查找樹出現了!
平衡二叉查找樹,算法由Adel'son-Vel'skii和 Landis兩位大神發明,同時也俗稱AVL 樹,來自兩位大神的姓名縮寫,特性如下:
- 它的左子樹和右子樹都是平衡二叉樹;
- 且它的左子樹和右子樹的深度之差的絕對值(平衡因子 ) 不超過1;
簡單的說,就是為了保證平衡,當前節點的左子樹、右子樹的高度差不超過1!
廢話也不多說了,直奔主題,算法思路如下!
二、算法思路
平衡二叉查找樹的查找思路,與二叉樹是一樣,每次查詢的時候對半分,只查詢一部分,以達到提供效率的目的,插入、刪除也一樣,最大的不同點:每次插入或者刪除之后,需要計算節點高度,然后按需進行調整!
如何調整呢?主要方法有:左旋轉、右旋轉!
下面我們分別來分析一下插入、刪除的場景調整。
2.1、插入場景
我們來分析一下插入的場景,如下:
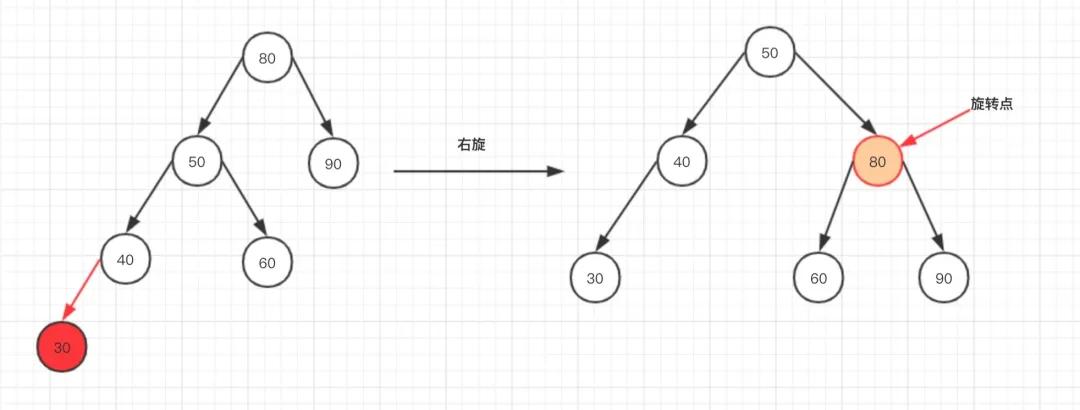
場景一
當我們在40的左邊或者右邊插入的時候,也就是50的左邊,只需繞80進行右旋轉,即可達到樹高度差不超過1!
場景二
當我們在60的左邊或者右邊插入的時候,也就是50的右邊,需要進行兩次旋轉,先會繞50左旋轉一次,再繞80右旋轉一次,即可達到樹高度差不超過1!
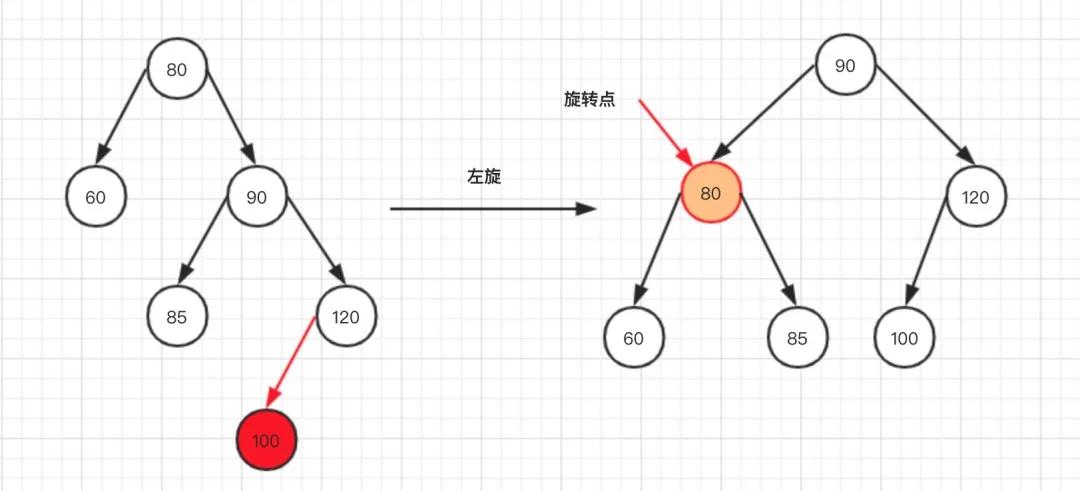
場景三
當我們在120的左邊或者右邊插入的時候,也就是90的右邊,只需繞80進行左旋轉,即可達到樹高度差不超過1!
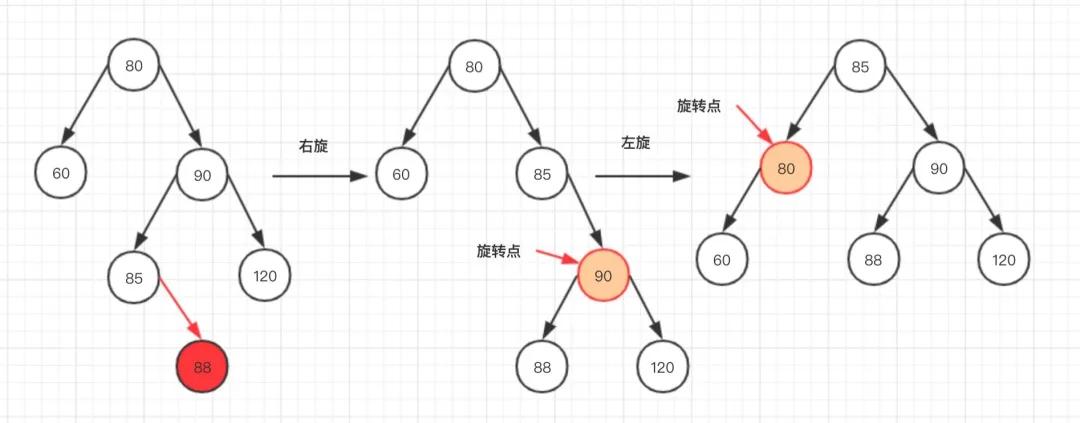
場景四
當我們在85的左邊或者右邊插入的時候,也就是90的左邊,需要進行兩次旋轉,先會繞90右旋轉一次,再繞80左旋轉一次,即可達到樹高度差不超過1!
總結
對于插入這種操作,總共其實只有這四種類型的插入,即:單次左旋轉、單次右旋轉、左旋轉-右旋轉、右旋轉-左旋轉,總結如下:
- 當插入節點位于需要旋轉節點的左節點的左子樹時,只需右旋轉;
- 當插入節點位于需要旋轉節點的左節點的右子樹時,需要左旋轉-右旋轉;
- 當插入節點位于需要旋轉節點的右節點的右子樹時,只需左旋轉;
- 當插入節點位于需要旋轉節點的右節點的左子樹時,需要右旋轉-左旋轉;
2.2、刪除場景
接下來,我們分析一下刪除場景!
其實,刪除場景跟二叉樹的刪除思路是一樣的,不同的是需要調整,刪除的節點所在樹,需要層層判斷節點的高度差是否大于1,如果大于1,就進行左旋轉或者右旋轉!
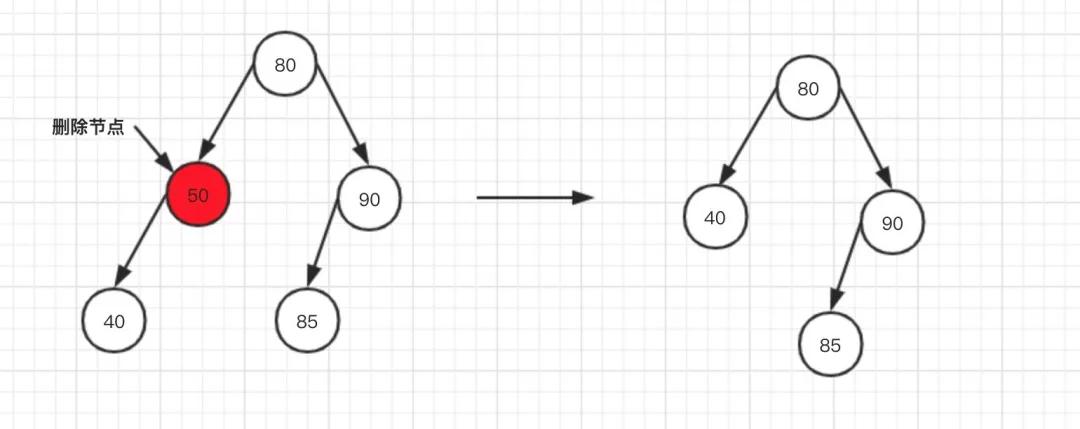
場景一
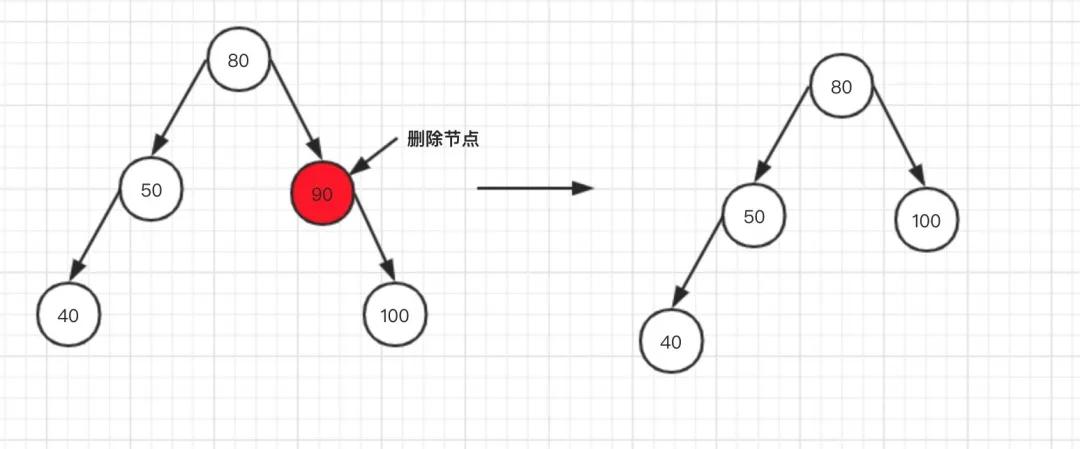
當刪除的節點,只有左子樹時,直接將左子樹轉移到上層即可!
場景二
當刪除的節點,只有右子樹時,直接將右子樹轉移到上層即可!
場景三
當刪除的節點,有左、右子樹時,因為當前節點的左子樹的最末端的右子樹或者當前節點的右子樹的最末端的左子樹,最接近當前節點,找到其中任意一個,然后將其內容替換并移除最末端節點,即可實現刪除!
總結
第三種場景稍微復雜了一些,但基本都是這么一個套路,與二叉樹不同的是,刪除之后需要判斷樹高,對超過1的進行調整,類似上面插入的左旋轉、右旋轉操作!
三、代碼實踐
接下來,我們從代碼層面來定義一下樹的實體結構,如下:
- 1public class AVLNode<E extends Comparable<E>> {
- 2
- 3 /**節點關鍵字*/
- 4 E key;
- 5
- 6 /**當前節點樹高*/
- 7 int height;
- 8
- 9 /**當前節點的左子節點*/
- 10 AVLNode<E> lChild = null;
- 11
- 12 /**當前節點的右子節點*/
- 13 AVLNode<E> rChild = null;
- 14
- 15 public AVLNode(E key) {
- 16 this.key = key;
- 17 }
- 18
- 19 @Override
- 20 public String toString() {
- 21 return "AVLNode{" +
- 22 "key=" + key +
- 23 ", height=" + height +
- 24 ", lChild=" + lChild +
- 25 ", rChild=" + rChild +
- 26 '}';
- 27 }
- 28}
我們創建一個算法類AVLSolution,完整實現如下:
- 1public class AVLSolution<E extends Comparable<E>> {
- 2
- 3 /**定義根節點*/
- 4 public AVLNode<E> root = null;
- 5
- 6 /**
- 7 * 插入
- 8 * @param key
- 9 */
- 10 public void insert(E key){
- 11 System.out.println("插入[" + key + "]:");
- 12 root = insertAVL(key,root);
- 13 }
- 14
- 15 private AVLNode insertAVL(E key, AVLNode<E> node){
- 16 if(node == null){
- 17 return new AVLNode<E>(key);
- 18 }
- 19 //左子樹搜索
- 20 if(key.compareTo(node.key) < 0){
- 21 //當前節點左子樹不為空,繼續遞歸向下搜索
- 22 node.lChild = insertAVL(key,node.lChild);
- 23 //出現不平衡,只會是左子樹比右子樹高,大于1的時候,就進行調整
- 24 if(getHeight(node.lChild) - getHeight(node.rChild) == 2){
- 25 if(key.compareTo(node.lChild.key) < 0){
- 26 //如果插入的節點位于當前節點的左節點的左子樹,進行單次右旋轉
- 27 node = rotateRight(node);
- 28 }else{
- 29 //如果插入的節點位于當前節點的左節點的右子樹,先左旋轉再右旋轉
- 30 node = rotateLeftRight(node);
- 31 }
- 32 }
- 33 }else if(key.compareTo(node.key) > 0){
- 34 //當前節點右子樹不為空,繼續遞歸向下搜索
- 35 node.rChild = insertAVL(key,node.rChild);
- 36 //出現不平衡,只會是右子樹比左子樹高,大于1的時候,就進行調整
- 37 if(getHeight(node.rChild) - getHeight(node.lChild) == 2){
- 38 if(key.compareTo(node.rChild.key) < 0){
- 39 //如果插入的節點位于當前節點的右節點的左子樹,先右旋轉再左旋轉
- 40 node = rotateRightLeft(node);
- 41 }else{
- 42 //如果插入的節點位于當前節點的右節點的右子樹,進行單次左旋轉
- 43 node = rotateLeft(node);
- 44 }
- 45 }
- 46 } else{
- 47 //key已經存在,直接返回
- 48 }
- 49 //因為節點插入,樹高發生變化,更新節點高度
- 50 node.height = updateHeight(node);
- 51 return node;
- 52 }
- 53
- 54 /**
- 55 * 刪除
- 56 * @param key
- 57 */
- 58 public void delete(E key){
- 59 root = deleteAVL(key,root);
- 60 }
- 61
- 62 private AVLNode deleteAVL(E key, AVLNode<E> node){
- 63 if(node == null){
- 64 return null;
- 65 }
- 66 if(key.compareTo(node.key) < 0){
- 67 //左子樹查找
- 68 node.lChild = deleteAVL(key,node.lChild);
- 69 //可能會出現,右子樹比左子樹高2
- 70 if (getHeight(node.rChild) - getHeight(node.lChild) == 2){
- 71 node = rotateLeft(node);
- 72 }
- 73 } else if(key.compareTo(node.key) > 0){
- 74 //右子樹查找
- 75 node.rChild = deleteAVL(key, node.rChild);
- 76 //可能會出現,左子樹比右子樹高2
- 77 if (getHeight(node.lChild) - getHeight(node.rChild) == 2){
- 78 node = rotateRight(node);
- 79 }
- 80 }else{
- 81 //找到目標元素,刪除分三種情況
- 82 //1.當前節點沒有左子樹,直接返回當前節點右子樹
- 83 //2.當前節點沒有右子樹,直接返回當前節點右子樹
- 84 //3.當前節點有左子樹、右子樹的時候,尋找當前節點的右子樹的最末端的左子樹,進行替換和移除
- 85 if(node.lChild == null){
- 86 return node.rChild;
- 87 }
- 88 if(node.rChild == null){
- 89 return node.lChild;
- 90 }
- 91 //找到當前節點的右子樹的最末端的左子樹,也就是右子樹最小節點
- 92 AVLNode<E> minLChild = searchDeleteMin(node.rChild);
- 93 //刪除最小節點,如果高度變化,進行調整
- 94 minLChild.rChild = deleteMin(node.rChild);
- 95 minLChild.lChild = node.lChild;//將當前節點的左子樹轉移到最小節點上
- 96
- 97 node = minLChild;//覆蓋當前節點
- 98 //因為是右子樹發生高度變低,因此可能需要調整
- 99 if(getHeight(node.lChild) - getHeight(node.rChild) == 2){
- 100 node = rotateRight(node);
- 101 }
- 102 }
- 103 node.height = updateHeight(node);
- 104 return node;
- 105 }
- 106
- 107 /**
- 108 * 搜索
- 109 * @param key
- 110 * @return
- 111 */
- 112 public AVLNode<E> search(E key){
- 113 return searchAVL(key, root);
- 114 }
- 115
- 116 private AVLNode<E> searchAVL(E key, AVLNode<E> node){
- 117 if(node == null){
- 118 return null;
- 119 }
- 120 //左子樹搜索
- 121 if(key.compareTo(node.key) < 0){
- 122 return searchAVL(key, node.lChild);
- 123 }else if(key.compareTo(node.key) > 0){
- 124 return searchAVL(key, node.rChild);
- 125 } else{
- 126 //key已經存在,直接返回
- 127 return node;
- 128 }
- 129 }
- 130
- 131 /**
- 132 * 查找需要刪除的元素
- 133 * @param node
- 134 * @return
- 135 */
- 136 private AVLNode<E> searchDeleteMin(AVLNode<E> node){
- 137 if (node == null){
- 138 return null;
- 139 }
- 140 while (node.lChild != null){
- 141 node = node.lChild;
- 142 }
- 143 return node;
- 144 }
- 145
- 146 /**
- 147 * 刪除元素
- 148 * @param node
- 149 * @return
- 150 */
- 151 private AVLNode<E> deleteMin(AVLNode<E> node){
- 152 if(node == null){
- 153 return null;
- 154 }
- 155 if (node.lChild == null){
- 156 return node.rChild;
- 157 }
- 158 //移除最小節點
- 159 node.lChild = deleteMin(node.lChild);
- 160 //此時移除的是左節點,判斷是否平衡高度被破壞
- 161 if(getHeight(node.rChild) - getHeight(node.lChild) == 2){
- 162 //進行調整
- 163 node = rotateLeft(node);
- 164 }
- 165 return node;
- 166
- 167 }
- 168
- 169 /**
- 170 * 單次左旋轉
- 171 * @param node
- 172 * @return
- 173 */
- 174 private AVLNode<E> rotateLeft(AVLNode<E> node){
- 175 System.out.println("節點:" + node.key + ",單次左旋轉");
- 176 AVLNode<E> x = node.rChild;//獲取旋轉節點的右節點
- 177 node.rChild = x.lChild;//將旋轉節點的右節點的左節點轉移,作為旋轉節點的右子樹
- 178 x.lChild = node;//將旋轉節點作為旋轉節點的右子樹的左子樹
- 179
- 180 //更新調整節點高度(先調整旋轉節點node)
- 181 node.height = updateHeight(node);
- 182 x.height = updateHeight(x);
- 183 return x;
- 184 }
- 185
- 186 /**
- 187 * 單次右旋轉
- 188 * @return
- 189 */
- 190 private AVLNode<E> rotateRight(AVLNode<E> node){
- 191 System.out.println("節點:" + node.key + ",單次右旋轉");
- 192 AVLNode<E> x = node.lChild;//獲取旋轉節點的左節點
- 193 node.lChild = x.rChild;//將旋轉節點的左節點的右節點轉移,作為旋轉節點的左子樹
- 194 x.rChild = node;//將旋轉節點作為旋轉節點的左子樹的右子樹
- 195
- 196 //更新調整節點高度(先調整旋轉節點node)
- 197 node.height = updateHeight(node);
- 198 x.height = updateHeight(x);
- 199 return x;
- 200 }
- 201
- 202 /**
- 203 * 左旋轉-右旋轉
- 204 * @param node
- 205 * @return
- 206 */
- 207 private AVLNode<E> rotateLeftRight(AVLNode<E> node){
- 208 System.out.println("節點:" + node.key + ",左旋轉-右旋轉");
- 209 //先對當前節點的左節點進行左旋轉
- 210 node.lChild = rotateLeft(node.lChild);
- 211 //再對當前節點進行右旋轉
- 212 return rotateRight(node);
- 213 }
- 214
- 215 /**
- 216 * 右旋轉-左旋轉
- 217 * @param node
- 218 * @return
- 219 */
- 220 private AVLNode<E> rotateRightLeft(AVLNode<E> node){
- 221 System.out.println("節點:" + node.key + ",右旋轉-左旋轉");
- 222 //先對當前節點的右節點進行右旋轉
- 223 node.rChild = rotateRight(node.rChild);
- 224 return rotateLeft(node);
- 225
- 226 }
- 227
- 228 /**
- 229 * 獲取節點高度,如果為空,等于-1
- 230 * @param node
- 231 * @return
- 232 */
- 233 private int getHeight(AVLNode<E> node){
- 234 return node != null ? node.height: -1;
- 235 }
- 236
- 237 /**
- 238 * 更新節點高度
- 239 * @param node
- 240 * @return
- 241 */
- 242 private int updateHeight(AVLNode<E> node){
- 243 //比較當前節點左子樹、右子樹高度,獲取節點高度
- 244 return Math.max(getHeight(node.lChild), getHeight(node.rChild)) + 1;
- 245 }
- 246
- 247 /**
- 248 * 前序遍歷
- 249 * @param node
- 250 */
- 251 public void frontTreeIterator(AVLNode<E> node){
- 252 if(node != null){
- 253 System.out.println("key:" + node.key);
- 254 frontTreeIterator(node.lChild);//遍歷當前節點左子樹
- 255 frontTreeIterator(node.rChild);//遍歷當前節點右子樹
- 256 }
- 257 }
- 258
- 259 /**
- 260 * 中序遍歷
- 261 * @param node
- 262 */
- 263 public void middleTreeIterator(AVLNode<E> node){
- 264 if(node != null){
- 265 middleTreeIterator(node.lChild);//遍歷當前節點左子樹
- 266 System.out.println("key:" + node.key);
- 267 middleTreeIterator(node.rChild);//遍歷當前節點右子樹
- 268 }
- 269 }
- 270
- 271 /**
- 272 * 后序遍歷
- 273 * @param node
- 274 */
- 275 public void backTreeIterator(AVLNode<E> node){
- 276 if(node != null){
- 277 backTreeIterator(node.lChild);//遍歷當前節點左子樹
- 278 backTreeIterator(node.rChild);//遍歷當前節點右子樹
- 279 System.out.println("key:" + node.key);
- 280 }
- 281 }
- 282
- 283}
測試代碼,如下:
- 1public class AVLClient {
- 2
- 3 public static void main(String[] args) {
- 4 //創建一個Integer型的數據結構
- 5 AVLSolution<Integer> avlTree = new AVLSolution<Integer>();
- 6
- 7 //插入節點
- 8 System.out.println("========插入元素========");
- 9 avlTree.insert(new Integer(100));
- 10 avlTree.insert(new Integer(85));
- 11 avlTree.insert(new Integer(120));
- 12 avlTree.insert(new Integer(60));
- 13 avlTree.insert(new Integer(90));
- 14 avlTree.insert(new Integer(80));
- 15 avlTree.insert(new Integer(130));
- 16 System.out.println("========中序遍歷元素========");
- 17
- 18 //中序遍歷
- 19 avlTree.middleTreeIterator(avlTree.root);
- 20 System.out.println("========查找key為100的元素========");
- 21
- 22 //查詢節點
- 23 AVLNode<Integer> searchResult = avlTree.search(120);
- 24 System.out.println("查找結果:" + searchResult);
- 25 System.out.println("========刪除key為90的元素========");
- 26
- 27 //刪除節點
- 28 avlTree.delete(90);
- 29 System.out.println("========再次中序遍歷元素========");
- 30
- 31 //中序遍歷
- 32 avlTree.middleTreeIterator(avlTree.root);
- 33 }
- 34}
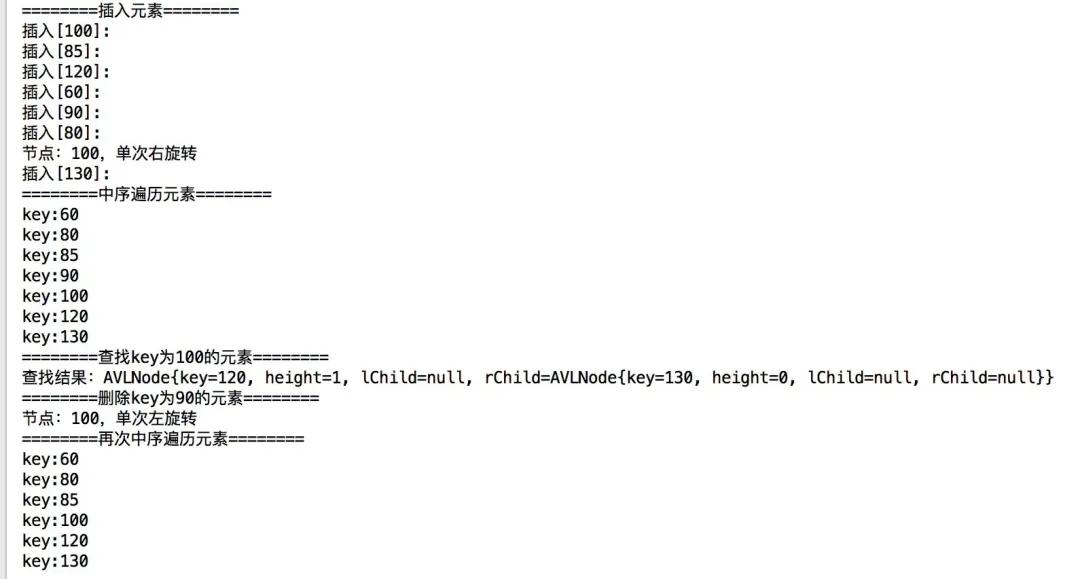
輸出結果如下:
四、總結
平衡二叉樹查找樹,俗稱AVL樹,在查詢的時候,操作與普通二叉查找樹上的查找操作相同;插入的時候,每一次插入結點操作最多只需要單旋轉或雙旋轉;如果是動態刪除,刪除之后必須檢查從刪除結點開始到根結點路徑上的所有結點的平衡因子,也就是高度差,如果超過1就需要調整,最多可能需要O(logN)次旋轉。
整體上來說,平衡二叉樹優于普通二叉查找樹!
五、參考
[1] 簡書 - nicktming - 二叉平衡樹: https://www.jianshu.com/p/22c00b3731f5
[2] iteye - Heart.X.Raid - 平衡二叉查找樹 [AVL]: https://www.iteye.com/blog/hxraid-609949