本文經AI新媒體量子位（公眾號ID:QbitAI）授權轉載，轉載請聯系出處。

美國持續封鎖，華為的技術自研，已經深入到了AI底層算法層面上，并開始將研究成果面向業界開源。

剛剛，華為諾亞實驗室開源Disout算法（地址在文末），直接對標谷歌申請專利的Dropout算法。

而且，在多項任務上，華為的新算法都超過了Dropout。比如，在ImageNet上訓練的ResNet-50可以達到78.76%的準確率，而谷歌Dropout系列方法僅為76.8%。

這一算法背后的論文，已被AAAI 2020收錄，并對外公開。華為到底提出的Disout到底如何，也得以呈現。

華為自研Disout：多項AI任務超越Dropout

在申請專利時，谷歌將Dropout定義為“解決神經網絡過擬合的系統和方法”。

其核心的思路是，訓練神經網絡前向傳播過程中，Dropout能讓某個神經元的激活值以一定的概率p停止工作，也就是“Drop”（丟棄），提升模型穩定性，來緩解過擬合現象。

而Disout是提出的新型替代方案，是一種通過研究特征圖擾動來增強深度神經網絡的泛化能力的方法。

簡單來說，就是根據網絡中間層的Rademacher 復雜度（ERC），確定給定深度神經網絡的泛化誤差上界。

并將擾動引入特征圖，來降低網絡的Rademacher復雜度，從而提高其泛化能力。

它們之間的區別可以用下面這張圖來展示——也就是對輸出特征進行擾動，而不是丟棄。

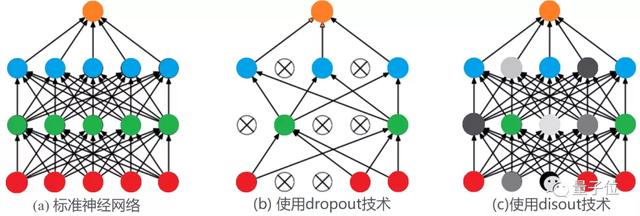
相比之下，華為的方法效果更好。

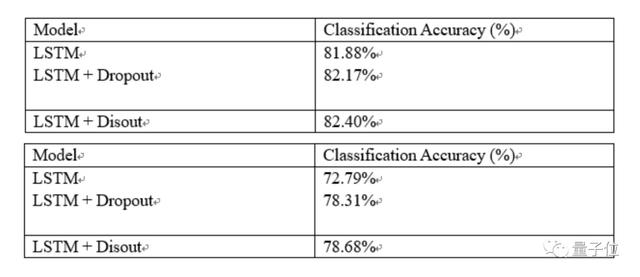
Disout不但在傳統視覺任務上表現優異，超越谷歌Dropout性能，在NLP任務以及語音處理任務上，同樣具備有效性。

接下來，就讓我們一起看下Disout在各個數據集上與Dropout系列方法的對比。

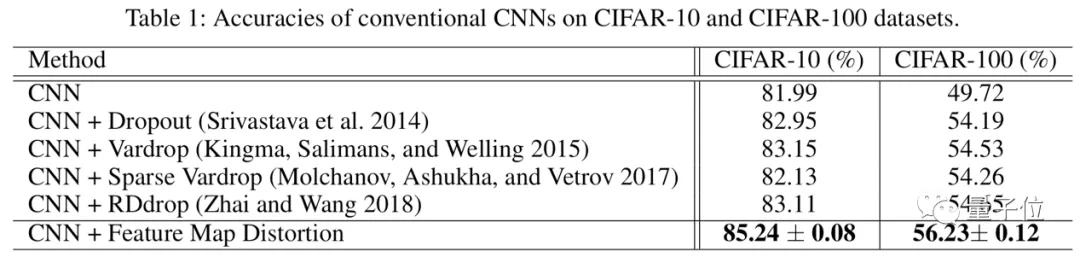
首先，CIFAR-10的和CIFAR-100數據上的測試準確率對比。

全連接層實驗中，華為所提出的特征圖擾動方法，訓練CNN達到85.24％的準確度，相比于最新的RDdrop方法，測試準確率分別在CIFAR-10和CIFAR-100數據集上提高了2.13％和1.58％。

華為研究人員表示，他們提出的Disout方法可以有效地降低經驗Rademacher的復雜度，同時保留模型的表示能力，從而具有較好的測試性能。

在卷積層實驗上，華為的方法可以適用于卷積層，提高深度神經網絡的性能，而且優于DropBlock方法，性能分別提高了0.32％和0.63％。

ImageNet 數據集實驗中結果也顯示，華為提出的特征擾動方法不僅可以替換常規的dropout方法提高深度神經網絡的性能，而且可以提升最近提出的Dropblock方法的性能。

與傳統的dropout方法相比，Disout將準確性從76.80％提高到77.71％，Block Disout方法達到了78.76％的top-1準確率，超過其他現有技術。

華為研究人員說，他們的方法可以在提高泛化能力并保留原始特征的有用信息。

此外，他們還在文本數據集IMDB和語音數據集UrbanSound8k上進行了實驗，結果如下（上為文本、下為語音）：

核心突破：對輸出特征進行擾動，而不是丟棄

那么，具體又是如何做到的呢？我們一起來了解一下泛化理論。

泛化理研究的是期望風險與經驗風險之間的關系。

以圖像分類任務為例，總體期望風險R(fL)和訓練集上的經驗風險

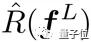
是：

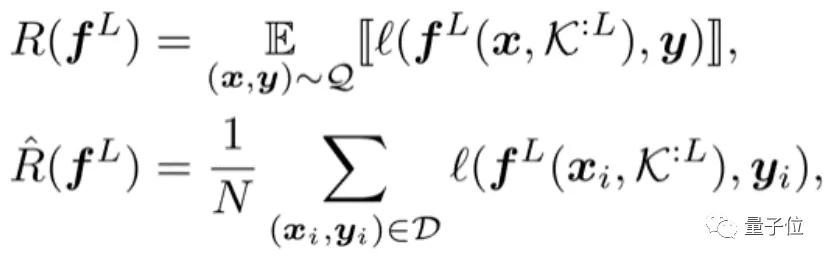
Rademacher經驗復雜度（ERC）被廣泛用于量化期望風險和經驗風險之間的差距，它的定義如定義1所示。

定義1：給定由分布Q成的個實例D= {(x,y)}的給定訓練數據集，網絡的經驗Rademacher復雜度定義為：

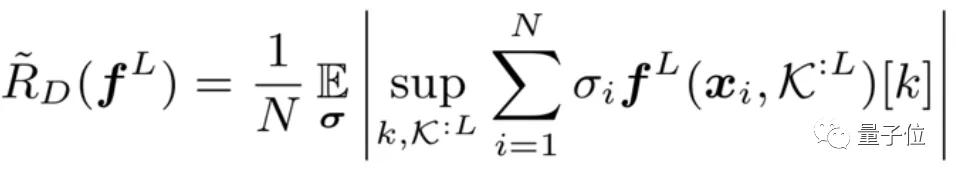
其中Rademacher變量是{-1，+ 1}中的獨立統一隨機變量。

使用經驗Rademacher復雜度和MaDiarmid不等式，可以通過定理1得出預期風險的上限。

定理1：給定 >0，對任意>0，至少以概率1−，對于所有的∈，滿足

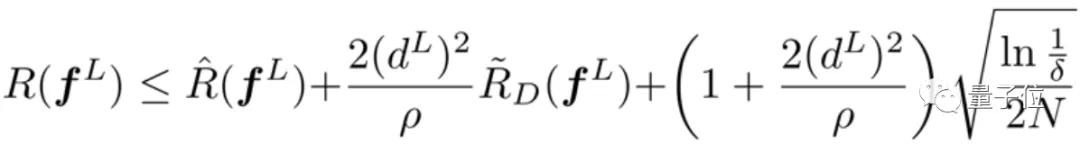
根據定理1，研究人員發現，期望風險和經驗風險之間的差距，可以借助特定神經網絡和數據集上的經驗Rademacher復雜度加以限制。

直接計算ERC比較難，因此通常在訓練階段使用ERC的上限或近似值，來獲得具有更好泛化的模型。

了解完泛化理論，就來看下特征圖擾動。

研究人員通過減少網絡的ERC來學習特征圖的擾動值，而不是固定擾動值。

通常，對具有輸入數據xi的第l層的輸出特征fL(xi)所采用的干擾操作可以表示為：

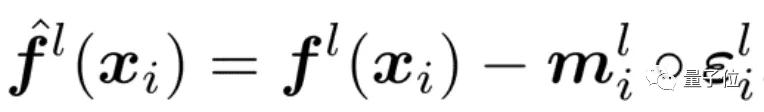
其中，εli是特征圖上的擾動 。

上面的等式中擾動的形式是在ERC指導下自行學習得到的。由于ERC是通過網絡最后一層的輸出計算出來的，直接使用它來指導擾動將非常困難。

因此，研究人員使用以下定理，通過網絡中間層的輸出來間接表達網絡的ERC：

定理 2 用Kl[k;:]表示權重矩陣Kl的第k行 ||・||p是向量的 p-norm。假設|| Kl[k;:] ||p ≤ Bl，網絡輸出的ERC 可以被中間特征的ERC限制：

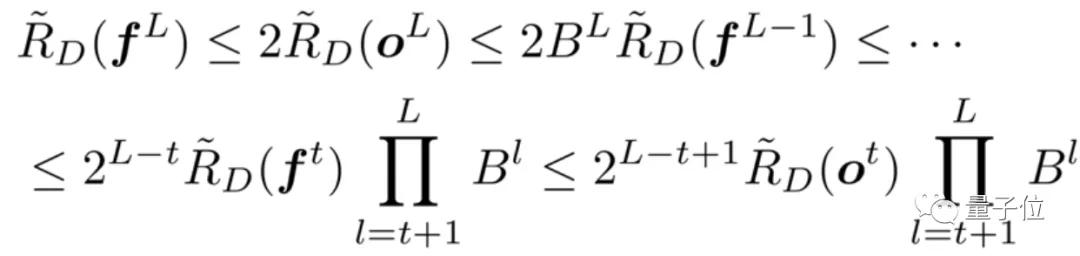
o 和 f 分別是在激活函數之前和之后的特征圖。令：

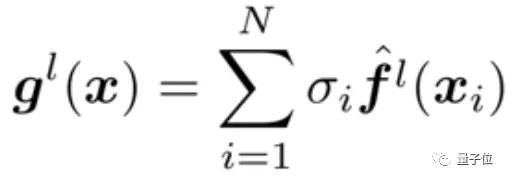
則：

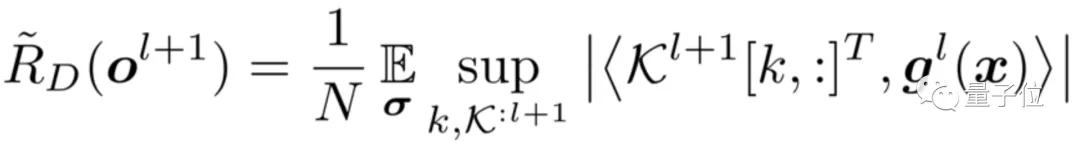
那么，最優的擾動，就可以通過求解下式得到：

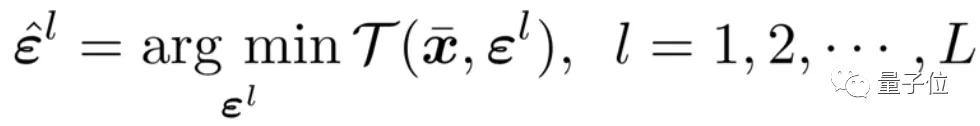
直觀地, 過于劇烈的擾動將破壞原始的特征并降低網絡的表示能力；而過小的擾動不能很好地起到正則化效果。

算法如下所示：

實習生一作，華為諾亞實驗室出品

這篇論文，一共有7名研究人員，分別來自北京大學、華為諾亞和悉尼大學，核心團隊來自華為諾亞實驗室。

一作是北京大學的唐業輝，這一研究是他在華為諾亞實驗室實習期間完成。

二作是王云鶴，華為諾亞方舟實驗室技術專家，也是唐業輝實習時的導師。

畢業于北京大學，在相關領域發表學術論文40余篇，包含NeurIPS、ICML、CVPR、ICCV、TPAMI、AAAI、IJCAI等。

主要從事邊緣計算領域的算法開發和工程落地，研究領域包含深度神經網絡的模型裁剪、量化、蒸餾和自動搜索等。

其他作者有來自華為諾亞實驗室的許奕星、許春景、北京大學的許超等人。

如果你對這項研究感興趣，請收好傳送門：

開源鏈接：https://github.com/huawei-noah/Disout