本文轉(zhuǎn)載自公眾號“讀芯術(shù)”(ID：AI_Discovery)。

機器學(xué)習(xí)已然成為許多領(lǐng)域的大熱詞。但其實，真正了解機器學(xué)習(xí)的人還是少數(shù)，大多數(shù)人屬于以下兩個陣營：

• 不懂機器學(xué)習(xí)算法;
• 知道算法是如何工作的，但不知道為什么會工作。

因此，本文試圖闡述算法的工作流程和內(nèi)容，盡力直觀地解釋其中的工作原理，希望能讓你對此有豁然開朗之感。

[[342820]]

決策樹

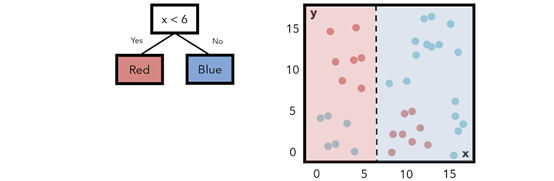
決策樹用水平線和垂直線劃分特征空間。下圖是一個簡單的決策樹，有一個條件節(jié)點和兩個類節(jié)點，表示一個條件以及判斷滿足該條件的節(jié)點屬于哪個類別。

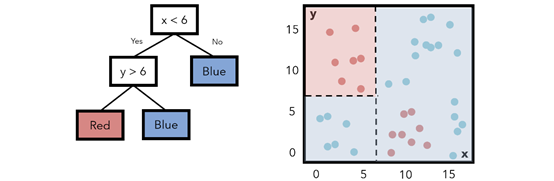
請注意，標記為不同顏色的字段與該區(qū)域內(nèi)實際是該顏色或熵的數(shù)據(jù)點之間有很多重疊。要以最小化熵構(gòu)造決策樹，這種情況下，可以添加一個額外的復(fù)雜層。如果加入另一個條件(x<6，y>6)，可以把相應(yīng)區(qū)域的點標為紅色。這個移動降低了熵值。

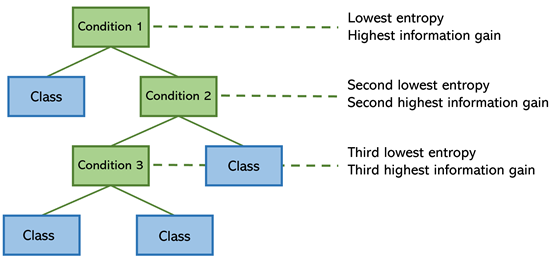
該算法在每個步驟中都試圖找到一種方法來構(gòu)建樹，使熵最小化。將熵的數(shù)量看作是“無序的”、“混亂的”，其對立面是“信息增益”——分頻器為模型添加信息和見解的多少，具有最高信息增益(以及最低熵)特征的，分割位于頂部。

這些條件的一維特征可能會被拆分，方式可能為：

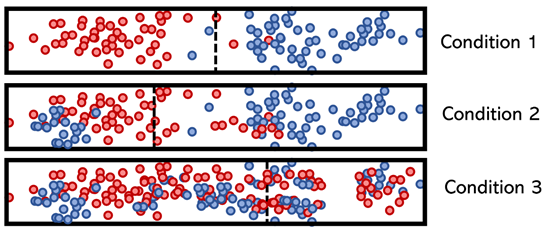
注意，條件1分離清晰，因此熵低，信息增益高。而條件 3就不同了，這就是它被放置在決策樹底部的原因。決策樹的構(gòu)造確保其輕量級。

隨機森林模型

隨機森林模型是決策樹的袋裝版本(引導(dǎo)聚合)，其主要含義是：每個決策樹都要經(jīng)過數(shù)據(jù)子集的訓(xùn)練，然后輸入每個模型之間的傳遞，其輸出通過如均值之類的函數(shù)以最終輸出。袋裝法(bagging)是一種綜合學(xué)習(xí)形式。

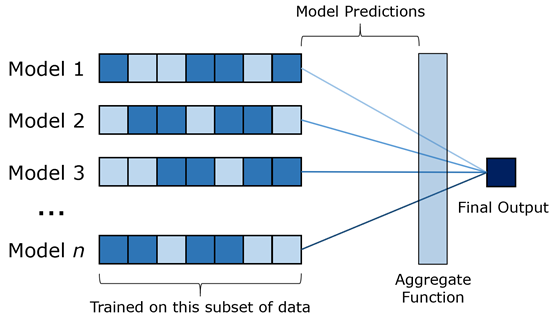
有很多類似的例子可以解釋隨機森林的有效性。以下是一個常見的例子：

你要決定下一頓去哪家餐館，需要他人的推薦，你必須回答“是或否”的問題，引導(dǎo)他們決定你去哪一家餐廳。你是選擇問一個朋友還是問幾個朋友，是普遍共識嗎?除非只有一個朋友，多數(shù)人會選擇問幾個朋友。這個類比告訴我們，每棵樹都有“思維多樣性”，它們選擇不同的數(shù)據(jù)，因此有不同的結(jié)果。

這個類比雖簡單明了，卻未引起Andre Ye的注意。現(xiàn)實生活中，單一朋友選項的經(jīng)驗比所有朋友的經(jīng)驗都要少，但在機器學(xué)習(xí)中，決策樹和隨機森林模型是根據(jù)相同的數(shù)據(jù)進行訓(xùn)練，因此體驗相同，集成模型實際上并沒有接收到任何新信息。如果你請一位無所不知的朋友推薦，他也不會有什么反對意見。

根據(jù)隨機提取數(shù)據(jù)子集以模擬人工“多樣性”的同一數(shù)據(jù)進行訓(xùn)練的模型，如何比對整個數(shù)據(jù)進行訓(xùn)練的模型表現(xiàn)更好?以具有重正等分布噪聲的正弦波為例，這一單個決策樹分類器自然是一個非常高方差的模型。

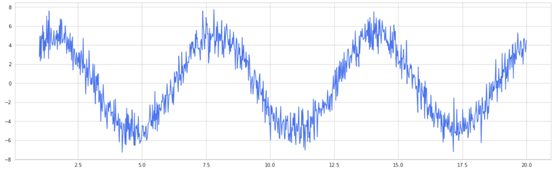
選擇 100個“近似器”，這些近似器隨機選擇正弦波上的點并生成正弦擬合，就像對數(shù)據(jù)子集進行訓(xùn)練的決策樹一樣。然后對這些擬合進行平均，形成袋形曲線，也就是一條更平滑的曲線。

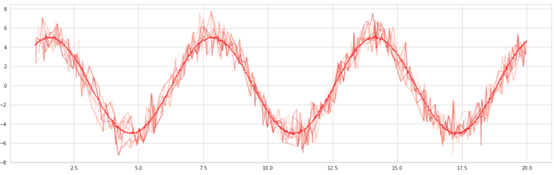
裝袋算法之所以有效，是因為它降低了模型的方差，并以人為方式使模型置信度更高，幫助提高泛化能力，這也是裝袋算法在低方差模型(如邏輯回歸)中不起作用的原因。

支持向量機

支持向量機試圖找到一個可以最好地劃分數(shù)據(jù)的超平面，依靠“支持向量”的概念來劃分兩個類別。

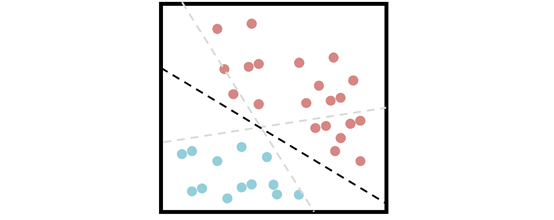
不幸的是，大多數(shù)據(jù)集并不是那么容易分離的。如果分離容易，SVM 可能就不是處理數(shù)據(jù)集的最佳算法了。考慮一維分離這樣的目標是沒有完美分隔線的，因為任何一個分離都會導(dǎo)致兩個單獨的類被歸為同一個類。

一個分裂的提議

SVM 能夠使用所謂的“內(nèi)核技巧”解決這類問題，將數(shù)據(jù)投射到新的維度，使分離任務(wù)更加容易。例如，創(chuàng)建一個新維度，僅定義它為 x^2(x是原始維度)：

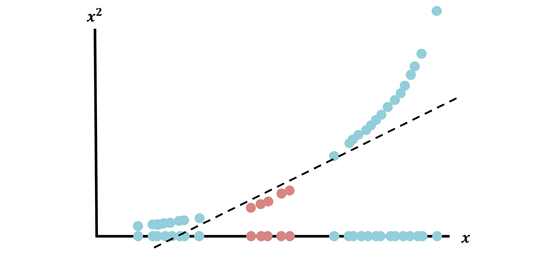
數(shù)據(jù)被投射到新的維度，每個數(shù)據(jù)點在兩個維度中表示為(x，x^)后，數(shù)據(jù)是完全可分離的。使用各種內(nèi)核(最普遍、多式非分體、sigmoid 和 RBF 內(nèi)核)、內(nèi)核技巧可以完成創(chuàng)建轉(zhuǎn)換空間的繁重任務(wù)，使分離任務(wù)變得簡單。

神經(jīng)網(wǎng)絡(luò)

神經(jīng)網(wǎng)絡(luò)是機器學(xué)習(xí)的巔峰。相關(guān)發(fā)現(xiàn)以及在此基礎(chǔ)上進行無限變化和改進，使其成為領(lǐng)域內(nèi)深度學(xué)習(xí)的主題。不可否認，神經(jīng)網(wǎng)絡(luò)仍然不完整(“神經(jīng)網(wǎng)絡(luò)是無人理解的矩陣乘法”)，但最簡單的解釋方法是通用近似定理(UAT)。

在其核心，每個監(jiān)督算法都試圖為數(shù)據(jù)的一些基本功能建模，通常是回歸平面或要素邊界。思考函數(shù)y=x2，它可以通過幾個步驟建模為任意精度。

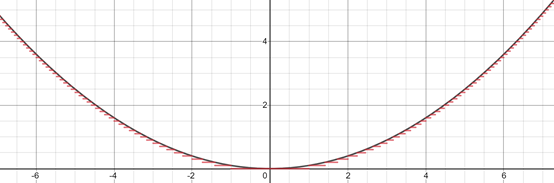
這就是神經(jīng)網(wǎng)絡(luò)所能做的，也許會稍微復(fù)雜并且超越水平步驟(如下圖二次線和線性線)來建模關(guān)系，但其核心就是一個分段函數(shù)近似器。

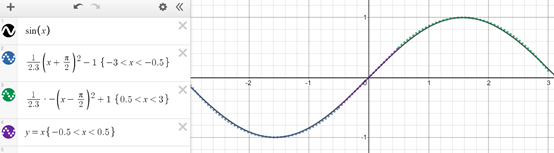
每個節(jié)點都委托給分段函數(shù)的一部分，網(wǎng)絡(luò)的目的是激活負責部分要素空間的特定神經(jīng)元。例如，如果要對是否留胡子的男性進行圖像分類，應(yīng)將幾個節(jié)點專門分配到經(jīng)常出現(xiàn)胡子的像素位置。在多維空間的某個地方，這些節(jié)點表示數(shù)值范圍。

"神經(jīng)網(wǎng)絡(luò)為什么工作"的問題仍然沒有答案，UAT沒有回答這個問題。但它指出神經(jīng)網(wǎng)絡(luò)在某些人的解釋下可以建模任何功能，可解釋的人工智能領(lǐng)域興起，通過激活最大化和靈敏度分析等方法回答這些問題。

[[342830]]

圖源：unsplash

這4種算法以及其他許多算法其實都是低緯度的，并且非常簡單。這就是機器學(xué)習(xí)領(lǐng)域的一個關(guān)鍵點，我們聲稱在人工智能中看到的許多“魔法”和“智能”，實際上是隱藏在高維表象下的一個簡單算法。

決策樹將區(qū)域拆分為正方形很簡單，但將高維空間拆分為超立方體則不簡單;SVM 通過執(zhí)行內(nèi)核技巧，提高從一維到二維的可分離性，但 SVM 在數(shù)百個維度的大數(shù)據(jù)集上做同樣的事情是難上加難。

我們對機器學(xué)習(xí)的欽佩和困惑是源于對高維空間缺乏理解，學(xué)習(xí)如何繞過高維空間，理解本地空間的算法，對直觀理解很有幫助。