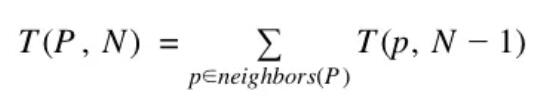有位外國小哥在自己的博客上通過解答一道面試題，發布了自己在谷歌擔任工程師和面試官的經驗，分享了對于科技公司面試者的一些建議。

[[347644]]

「金九銀十」的求職季也只剩下了一個尾巴，不知道正在求職的你結果如何呢？

如果你是一名學生或者正在申請技術類的工作，希望你在讀完這篇文章之后能夠更好地應對即將到來的面試。

面試「腦筋急轉彎」，你怎么答？

想象一個電話撥號盤，從某個位置開始只能以大寫字母 「L」的形狀移動: 水平移動兩步，垂直移動一步，或水平移動一步，垂直移動兩步:

假設您在鍵盤上只能使用這種方式來撥號，撥下一個鍵并進行下一跳。起始位置計算為正在撥號的鍵。

那么，從一個特定的起始位置開始，能以 N 跳的方式撥多少個不同的號碼？

回答的套路：由淺至深的討論

面試基本上分為兩部分: 首先找到一個該問題的算法解決方案，然后面試者用代碼來實現它。

在面試的整個過程中，面試官通常不是一個沉默的旁觀者: 在松弛的環境中花45分鐘設計和實現任何東西時間都不充足，更不用說在有壓力的情況下了。

面試官通常會讓面試者在討論中發揮帶頭作用，產生想法，提出解決問題的實例等，但作者有時也非常樂意在正確的方向上給予對方推動。

面試者的水平越高，他傾向于給出的暗示就越少，但是作者還沒有看到過一個候選人完全不需要他的參與。

作為一個面試官，通常不會坐視別人失敗，「我想寫盡可能多的積極的反饋，我會盡量給你機會讓我寫關于你的好東西，提示是我說：好吧，我給你一點提示」，只有這樣才能讓一些面試者繼續前進，看看他們對問題的其他部分有什么看法。

話雖如此，作者希望面試者聽到這個問題后的第一個行動應該是走到白板前，手工解決這個問題的一些小實例。

「永遠不要一頭扎進代碼里！解決小的實例可以讓你發現模式，觀察和邊緣情況，也有助于在你的頭腦中明確解決方案」。

舉個例子，假設起始位置從6開始，你有兩跳的機會。則序列將會是：

以上總共有六個序列。如果試著用鉛筆和紙來推導這些，總比只是盯著它靜靜地思考，會帶來更好的結果。 

黃銅答案：初級面試者通常給出的方案

Level 1：到達下一跳

作者作為面試官經常會感到驚訝的是，求職者經常會陷入計算鍵值的困境，其實恰恰可以從一個給定的位置跳到這個鍵值，也就是我們所說的鄰居（neighbors）。

作者的建議是: 當有疑問的時候，可以寫一個空的占位符，然后問面試官是否可以稍后實現它。

這個問題的復雜性不在于鄰居的計算，而是如何很好地計算完整的數字，任何花費在鄰居計算上的時間都被浪費掉了。

通常可以假設有一個函數會傳給鄰居值，如下圖所示：

當然，這個空函數功能最終也是需要被實現的，但前提是面試剩余的時間還足夠。

而且，如果問題的復雜性在其他地方的話，面試者通常不會因為要求使用空函數而被留下壞印象，面試官通常都會同意這種做法。

如果沒有別的復雜問題，面試官還會要求面試者實際執行它。

至于這里的鄰居函數，考慮到它從不改變，可以簡單地創建一個 map 并返回相應的值:

Level 2：遞歸生成數字

不管怎樣，我們來看看解決方案。也許你已經注意到這個問題可以通過列舉所有可能的數字并計算它們來解決，可以使用遞歸來生成這些值:

這是一種非常普遍的想法。然而，生成的數字并沒有真正的使用它們。這個問題要求的是數字計數，而不是數字本身。

一旦計算了一個數字，就再也不會重訪它了。作為一般的經驗法則，作者建議注意當解決方案計算一些不使用的東西時，在通常情況下可以把它刪除，然后得到一個更好的解決方案。

鉆石方案：高級一些的想法

Level 3：「不計數的計數」

怎樣才能在不產生電話號碼的情況下計算電話號碼呢？請注意，從 n 跳中給定的起始位置生成的數字計數等于從 n 跳中的每個相鄰位置生成的數字計數之和。

從數學角度來說，它是一個遞推關系式，看起來像這樣:

有很多實現使用了這個公式的思想，但是讓我們從我在面試中最常見的一個開始: 「樸素的遞歸方法」:

接下來這個問題會經常從面試中聽到: 「這個解決方案的復雜度是多少」。對于那些不知道的人來說，O(N)復雜度是一種速率，一個解決方案所需的計算量隨著函數輸入大小的變化而增長。對于這個問題，輸入的大小是跳數。

對于這種實現，每次遞歸調用 count _ sequences ( ) 至少兩次，因為每個鍵至少有兩個鄰居。由于我們遞歸的次數等于所需的跳數，并且每次調用時計算 _ sequences ()的調用數量至少翻了一番，因此運行時的復雜度至少為指數級。

接下來通常的做法就是解決時間復雜度太高的問題。

Level 4：降低復雜度

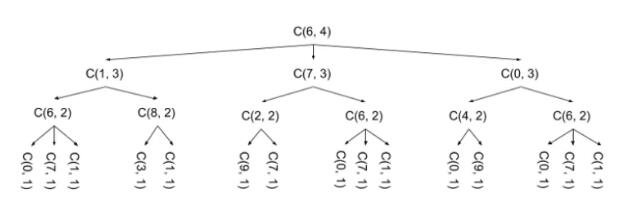
為了找到下一個函數，讓我們把這個函數調用的函數映射出來。讓我們考慮 count _ sequences (6,4)的情況。注意: 為了簡潔起見，使用 c 作為函數名:

注意這里 c (6,2)調用執行了三次，每次執行相同的計算并返回相同的值。這里關鍵的一點是，這些函數調用會重復調用，每次都返回相同的值。一旦你計算了他們的結果，就不需要重新計算了。

使用制表法可以解決這個問題 ，這基本上意味著我們可以記錄之前看到的函數調用的結果，并使用這些結果來代替重復工作。

這樣，當我們在調用圖中遇到不必要地重新計算整個子樹的位置時，可以立即返回已經計算的結果。下面是一個實現:

經過這樣的處理，復雜度就已經降到了線性的結果。

這個解決方案依舊有一些不足之處，主要的缺點是它是遞歸的。大多數語言都對其調用堆棧的最大大小進行限制，這意味著總是需要考慮可以支持最大的跳數。

Level 5：動態規劃

請注意，n 跳的結果僅依賴于 n-1 跳調用的結果。同時，緩存包含每個(非零)跳數的條目。

學過歸納法的人都知道，可以使用遞推關系式歸納步驟，可以從零跳數的基本情況開始，并歸納推導出所有大于零的值。下面是它的一個實現:

還有沒有比遞歸的深度優先解決方案更好的版本呢？不是很多，但也有一些。

首先，不是遞歸的意味著可以運行非常大的值而不會崩潰。

其次，使用常量內存，因為只需要兩個固定大小的數組，而不需要不斷增長的制表解決方案的緩存。

最后，仍然是線性時間復雜度: 可以在20秒內計算200,000跳。

在求職面試中設計和實現一個線性時間、常數空間的解決方案通常都會得到一個很好的結果。當作者使用這個問題進行面試時，經常給那些使用動態規劃方案的面試者一個很好的反饋。

最后，作者還列出了為了準備面試和今后的工作你應該養成的習慣:

1.始終從手推一個小實例開始。

2.注意你的解決方案做的哪些計算是不必要的。

3.清楚地使用遞歸。

4.知道你解決方案的O（N）。

5.總是尋找機會來回憶，如：編寫一個空函數。

現在正值「金九銀十」和校招季，希望大家都能找到自己心儀的工作！