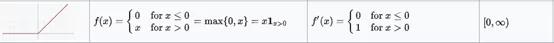本文轉載自公眾號“讀芯術”(ID：AI_Discovery)。

神經網絡和深度學習中的激活函數在激發隱藏節點以產生更理想的輸出方面起著重要作用，激活函數的主要目的是將非線性特性引入模型。

[[356462]]

在人工神經網絡中，給定一個輸入或一組輸入，節點的激活函數定義該節點的輸出。可以將標準集成電路視為激活功能的控制器，根據輸入的不同，激活功能可以“打開”(ON)或“關閉(OFF)”。

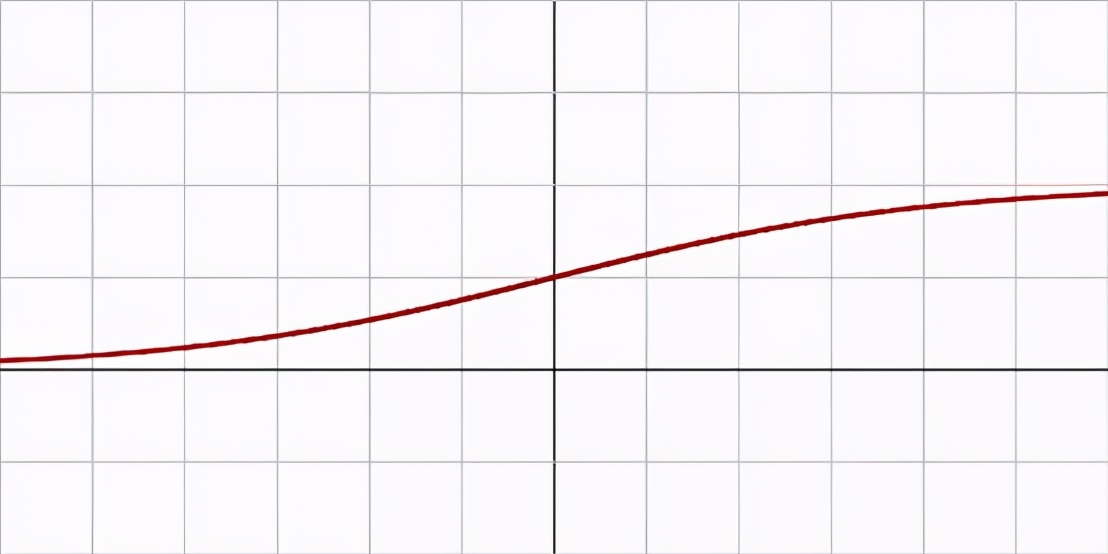
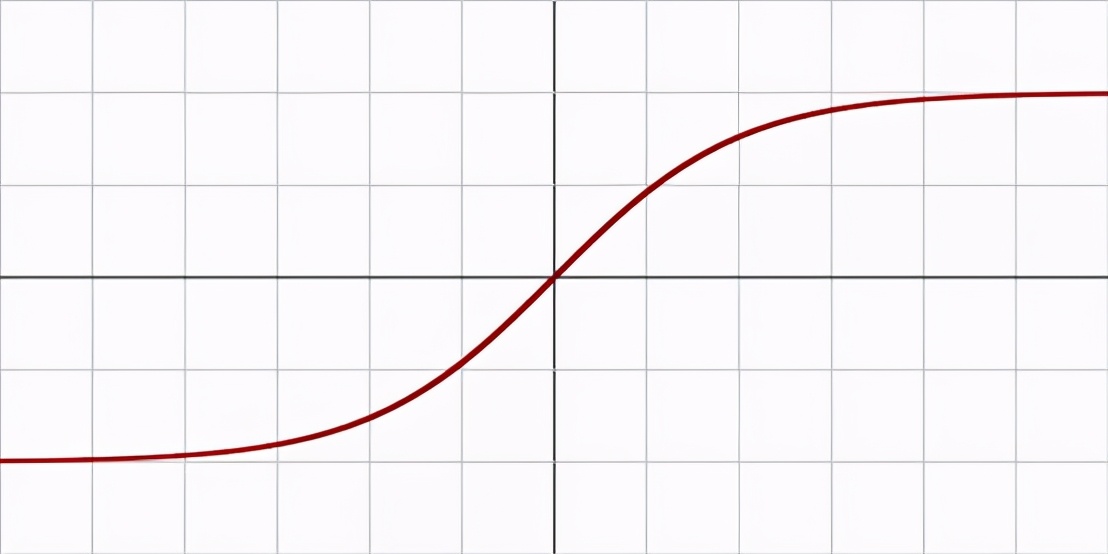
圖1：Sigmoid;圖2：tanh

Sigmoid和tanh是單調、可微的激活函數，在RELU出現前比較流行。然而，隨著時間的推移，這些函數會飽和，導致梯度消失。另一種常用的激活函數可以解決這一問題：直線修正單元(ReLU)。

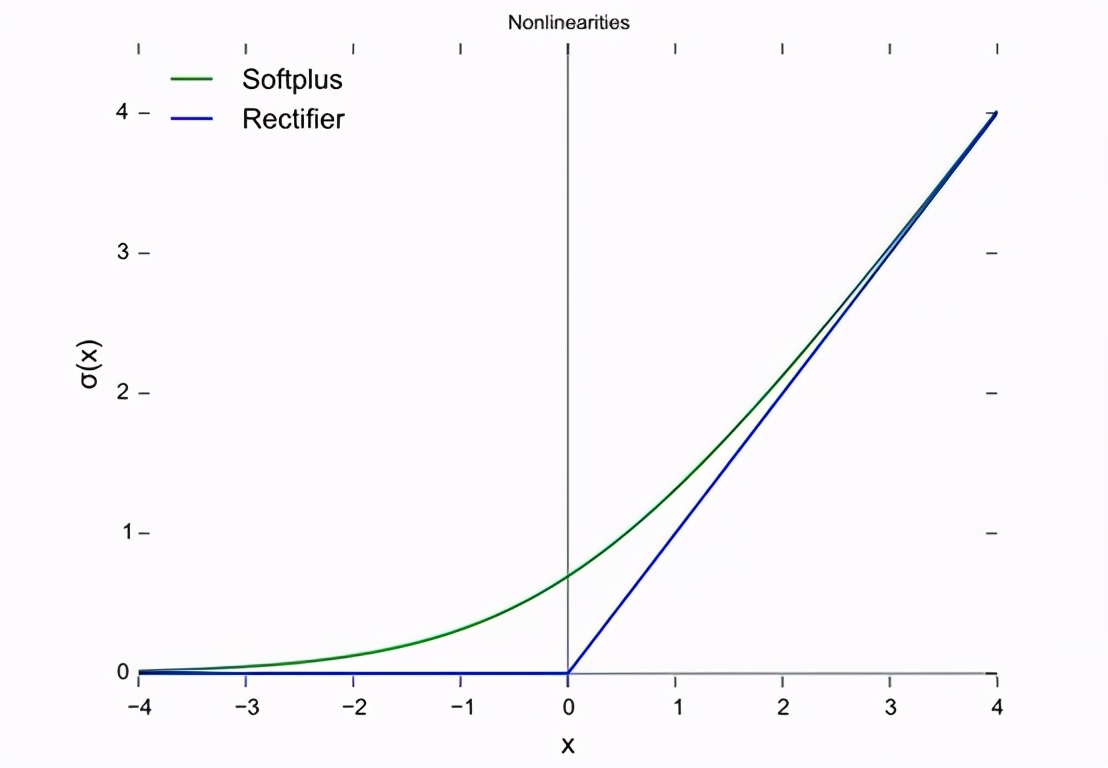
上圖中，藍線表示直線單元(ReLU)，而綠線是ReLU的變體，稱為Softplus。ReLU的其他變體包括LeakyReLU、ELU、SiLU等，用于提高某些任務的性能。

本文只考慮直線單元(ReLU)。因為默認情況下，它仍然是執行大多數深度學習任務最常用的激活函數。在用于特定目的時，其變體可能有輕微的優勢。

在2000年， Hahnloser等人首次將具有很強的生物學動機和數學證明的激活函數引入到一個動態網絡。相比于2011年之前廣泛使用的激活函數，如logistic sigmoid(靈感來自于概率理論和logistic回歸)及其更實用的tanh(對應函數雙曲正切)相比，這首次證明了該函數能夠更好地訓練更深層次的網絡。

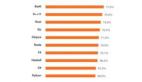
截止2017年，整流器是深度神經網絡中最受歡迎的激活函數。采用整流器的單元也稱為整流線性單元(ReLU)。

RELU的最大問題是在點0處是不可微。而研究人員傾向于使用sigmoid和tanh這種可微函數。但是在0點可微畢竟是特殊情況，所以到目前為止，ReLU還是深度學習的最佳激活功能，需要的計算量是非常小，計算速度卻很快。

在除0以外的所有點上，ReLU激活函數上都是可微的。對于大于0的值，僅考慮函數的最大值。可以這樣寫：

f(x) = max{0, z} 

簡單來說，也可以這樣：

if input > 0:    returninputelse:    return 0 

所有負數默認為0，并考慮正數的最大值。

對于神經網絡的反向傳播計算而言，ReLU的判別相對容易。唯一要做的假設是，在點0處的導數也被認為是0。這通常問題不大，而且在大多數情況下都ok。函數的導數就是斜率的值。負值的斜率是0.0，正值的斜率是1.0。

ReLU激活函數的主要優點是：

• 卷積層和深度學習：它們是卷積層和深度學習模型訓練中最常用的激活函數。
• 計算簡單：整流函數實現起來很簡單，只需要一個max()函數。
• 代表性稀疏性：整流器函數的一個重要優點是它能夠輸出一個真正的零值。
• 線性行為：當神經網絡的行為是線性或接近線性時，它更容易被優化。

然而，經過RELU單元的主要問題是所有的負值會立即變為0，這降低了模型對數據正確擬合或訓練的能力。

這意味著任何給ReLU激活函數的負輸入都會立即將圖中的值變為0。由于沒有適當地映射負值，這反過來會影響結果圖。不過，使用ReLU激活函數的不同變體(如LeakyReLU和前面討論的其他函數)，可以輕松解決這個問題。

這是一個簡短的介紹，幫你在深度學習技術時代了解整流線性單元及其重要性。畢竟，它比所有其他激活函數更受歡迎肯定是有原因的。