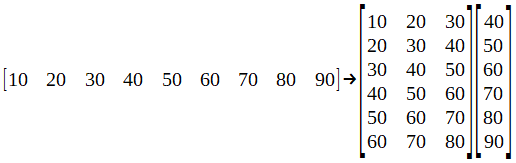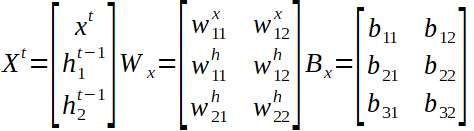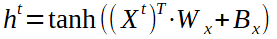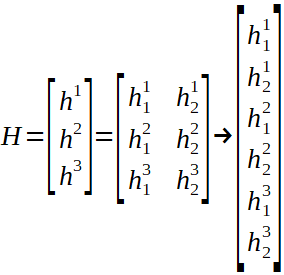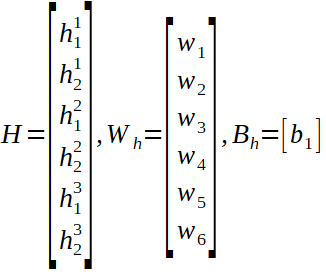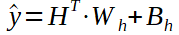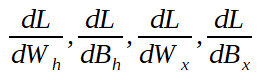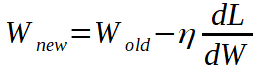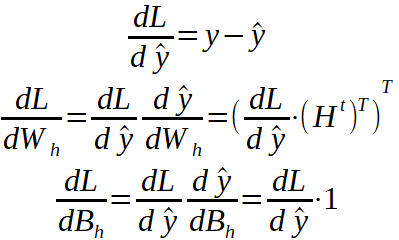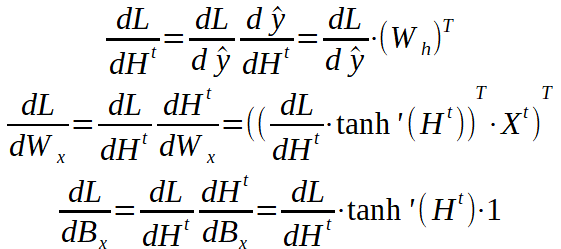RNN 從理論到PyTorch
讓我向您展示什么是RNN,在哪里使用,它們如何向前和向后傳播以及如何在PyTorch中使用它們。
大多數類型的神經網絡都可以對要對其進行訓練的樣本進行預測。一個主要的例子是MNIST數據集。像MLP這樣的常規神經網絡知道有10位數字,即使圖像與訓練網絡上的圖像非常不同,它也僅基于它們進行預測。
現在,假設我們可以通過提供9個有序數字的序列,并讓網絡猜測第10個數字,來利用這種網絡進行順序分析。網絡不僅會知道如何區分10位數字,而且還會知道從0到8的順序,下一位數字很可能是9。
在分析序列數據時,我們了解到,序列中的元素通常以某種方式相關,這意味著它們彼此依賴。因此,我們需要考慮每個元素以了解序列的想法。
劍橋大學出版社將序列定義為"事物或事件彼此跟隨的順序",或者最重要的是,"一系列相關事物或事件"。為了將此定義調整到深度學習的范圍內,順序是一組包含可訓練上下文的數據,刪除一些元素可能會使它無用。
但是序列包含什么?哪些分組數據可以具有上下文?以及如何提取上下文來利用神經網絡的力量?在進入神經網絡本身之前,讓我向您展示使用遞歸神經網絡(RNN)經常解決的兩種類型的問題。
時間序列預測
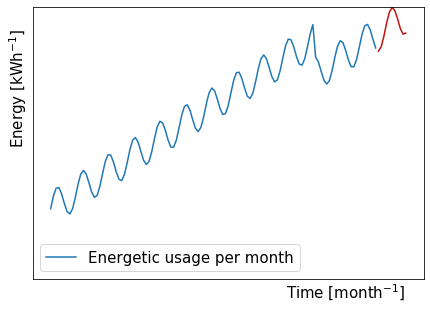
第一個示例是時間序列預測問題,其中我們用一系列現有數值(藍色)訓練神經網絡,以便預測未來的時間步長(紅色)。
如果我們按照這些家庭多年來的每月精力支出進行排序,我們可以看到正弦曲線趨勢呈上升趨勢,而突然下降。
正弦曲線部分的背景可能是整個夏季(從夏季到冬季)再到夏季的不同能量需求。精力充沛的支出增長可能來自使用更多的電器和設備,或者轉換為可能需要更多能源的更強大的電器和設備。突然跌倒的背景可能意味著一個人長大了足以離開家,而那個人所需的能量不再在那里。
您越了解上下文,通常可以通過連接輸入向量將更多信息提供給網絡,以幫助網絡理解數據。在這種情況下,對于每個月,我們可以將三個更多的值與能源聯系起來,這些價值包括電器和設備的數量,其能量效率以及家庭容納的人數。
自然語言處理
瑪麗騎自行車,自行車是____。
第二個例子是自然語言處理問題。這也是一個很好的例子,因為神經網絡必須考慮現有句子提供的上下文來完成它。
假設我們的網絡經過訓練,可以用所有格代詞完成句子。一個受過良好訓練的網絡將理解該句子是用第三人稱單數構成的,并且Mary最有可能是女性名字。因此,預測代詞應該是"她的"而不是男性的"他的"或復數的"他們的"。
現在,我們已經看到了兩個排序數據的例子,讓我們探索網絡向前和向后傳播的過程。
RNN配置
如我們所見,RNN從序列中提取信息以提高其預測能力。
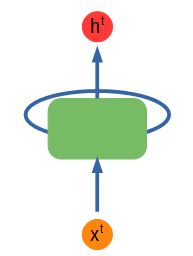
> Simple recurrent network diagram. Figure by author.
上面顯示了一個簡單的RNN圖。綠色節點輸入一些輸入x ^ t并輸出一些值h ^ t,該值也被饋送到該節點,再次包含從輸入中收集的信息。不管饋入節點的內容有什么模式,它都會學習并保留該信息以供下一次輸入。上標t代表時間步長。
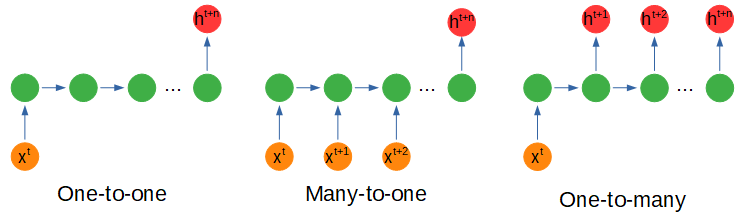
> Recurrent network configurations. Figure by author.
根據輸入或輸出的形狀,神經網絡的配置會有一些變化,稍后我們將了解節點內部會發生什么。
多對一配置是指我們以不同的時間步長輸入多個輸入以獲得一個輸出時,這可能是在電影場景的各個幀中捕獲的情感分析。
一對多使用一個輸入來獲取多個輸出。例如,我們可以使用多對一配置對表達某種情感的詩歌進行編碼,并使用一對多配置來創建具有相同情感的新詩行。
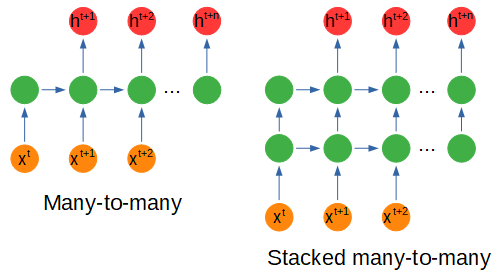
多對多使用多個輸入來獲取多個輸出,例如使用一系列值(例如在能量使用中)并預測未來的十二個月而不是一個月。
堆疊配置只是一個具有多個隱藏節點層的網絡。
RNN前傳
為了了解神經網絡節點內部發生的情況,我們將使用一個簡單的數據集作為"時間序列預測"示例。貝婁是價值的完整序列,它是作為培訓和測試數據集而進行的重組。
我從這個網站上拿了這個例子,這是一般而言深度學習的重要資源。現在,讓我們將數據集分成批次。
我在這里沒有顯示它,但不要忘記應該對數據集進行規范化。這很重要,因為神經網絡對數據集值的大小很敏感。
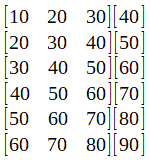
這個想法是預測未來的價值。因此,假設我們選擇了該批次的第一行:[10 20 30],在訓練了我們的網絡之后,我們應該得到40的值。要測試神經網絡,可以將向量輸入[70 80 90],并期望獲得一個如果網絡訓練有素,則值接近100。
我們將使用多對一配置,分別提供每個序列的三個時間步。當使用遞歸網絡時,輸入值不是進入網絡的唯一值,還有一個隱藏的數組,該數組的結構將在節點之間傳遞序列的上下文。我們將其初始化為零數組,并將其連接到輸入。它的尺寸(1 x 2)是個人選擇,只是使用與1 x 1步進輸入不同的尺寸。
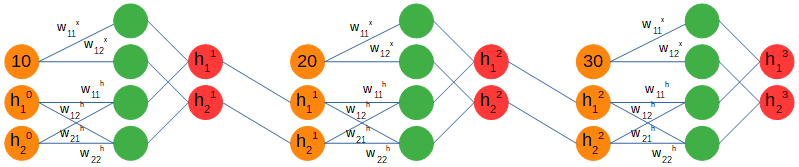
> Recurrent forward pass. Figure by author.
仔細觀察,我們可以看到權重矩陣分為兩部分。第一個處理輸入創建兩個輸出,第二個處理隱藏數組創建兩個輸出。然后將這兩組輸出加在一起,并獲得一個新的隱藏數組,其中包含來自第一個輸入(10)的信息,并將其饋送到下一個時間步輸入(20)。應當注意,權重和偏差矩陣在時間步長之間是相同的。
上面表示了全局輸入向量X ^ t,權重矩陣W和偏置矩陣B以及隱藏數組的計算。僅剩一個步驟才能完成前進。我們正在嘗試預測一個未來的價值,我們有三個隱藏的數組,每個輸入的信息作為輸出,因此我們需要將它們轉換為單個值,希望在經過許多次培訓后才是正確的值。
通過連接并重塑數組,我們可以附加一個線性層來計算最終結果。完整的網絡具有以下形式:
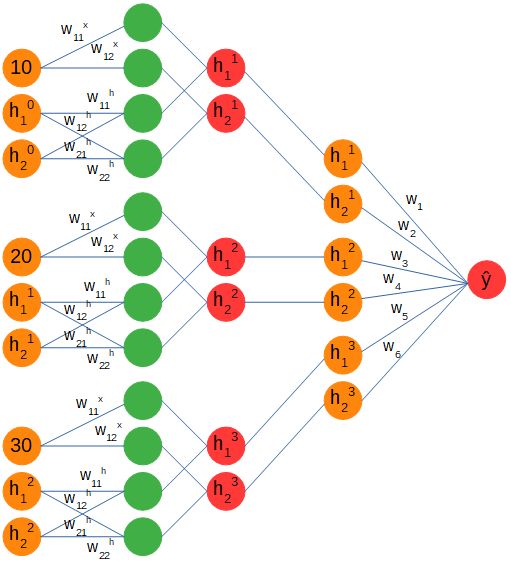
> Full recurrent diagram. Figure by author.
您可以看到多對一配置嗎?我們從一個序列中饋入三個輸入,它們的上下文由權重和偏差矩陣捕獲,并存儲在一個隱藏的數組中,該數組在每個時間步都用新信息更新。最終,存儲在隱藏數組中的上下文將經歷另一組權重和偏差,并且在將序列的所有時間步長輸入到網絡之后,將輸出一個值。
我們可以看到隱藏狀態的線性形式以及線性層的權重和偏差矩陣,以及預測值的計算(y hat)。
現在,這是RNN的前向傳播,但我們仍然沒有看到向后傳遞。
RNN向后傳遞
向后傳播是訓練每個神經網絡的非常重要的一步。在此,預測輸出和實際值之間的誤差朝著神經網絡傳播,目的是改善權重和偏差,以便每次迭代都能獲得更好的預測。
在大多數情況下,此步驟由于其復雜性而被忽略了。在提及重要內容的同時,我將向您提供一個盡可能簡單的解釋。
向后傳遞是使用微積分的鏈法則從損耗到所有權重和偏差參數的一系列推導。這意味著我們最終需要以下值(如果是多維的,則為數組):
如果您不熟悉一階導數的數學含義,但實際上,當一階導數為零時,我通常建議您閱讀有關梯度下降的文章,這通常意味著我們在系統中找到了一個最小值,并且理想情況下我們將無法進一步改善它。
這里需要注意的一點是:零也可能是最大值,它是不穩定的,不應在那里進行優化,或者是鞍點,其本身也不是很穩定。最小值可以是全局值(函數的最小值)或局部值。這對我的解釋并不重要,但是如果您想了解更多信息,可以查找一下!
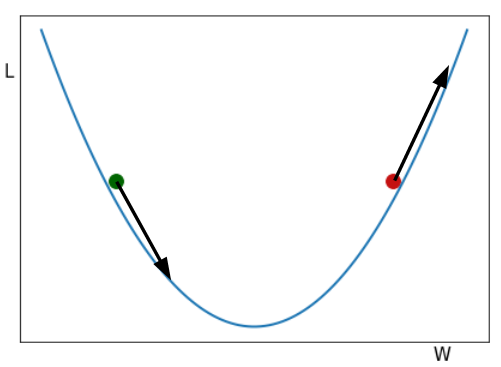
> Gradient Descent example. Two balls rolling down the hill. Figure by author.
您在圖片中看到的是兩個球從山谷中滾下來。從視覺上看,一階導數給了我們山坡的大小。如果我們沿W軸增加的方向(從左到右)行進,則對綠色球的傾斜度為負(向下),對于紅色球的傾斜度為正(向上)。
仔細閱讀下一段,然后根據需要返回到該圖。
如果我們希望損失最小,我們希望球到達山谷的最低點。W代表權重和偏差的值,因此,如果我們處于綠色球的位置,我們將減去負導數的一部分(使其為正值)到綠色球的W位置,將其向右移動并減去一部分將紅色球的W位置向左移動的正導數(使其變為負數),以使兩個球都接近最小值。
從數學上講,我們有以下內容:
η調整我們用來更新權重和偏差的導數的比例。
現在,繼續進行向后傳遞問題。我將介紹從損失到所有參數的鏈式導數,我們將看到每種導數代表什么。重要的是要牢記上面介紹的各層的方程式以及它們的參數矩陣。
要記住的一件事是,我們要查找的四個一階導數數組的形狀必須與我們要更新的參數相同。例如,陣列dL / dW_h的形狀必須與權重陣列W_h相同。上標T表示矩陣已轉置。
我們一直追溯到線性層的參數。因為我們將隱藏狀態數組重塑為線性向量,所以我們應將dL / dH ^ t重塑為串聯的隱藏狀態數組的原始形狀。目前,它是一個6 x 1的數組,但從循環圖層計算得出的隱藏數組的形狀是3 x 2。我們還將所有全局輸入連接在一起(t = 1、2和3),現在我們可以繼續進行反向傳遞了。
現在剩下要做的就是應用我們之前看到的Gradient Descent方程來更新參數,并且模型可以進行下一次迭代了。讓我們看看如何使用PyTorch構建簡單的RNN。
PyTorch的RNN
使用PyTorch非常簡單,因為我們真的不需要擔心向后傳遞。但是,即使我們不直接使用它,我仍然相信了解它的工作原理很重要。
繼續,如果我們參考PyTorch的文檔,我們可以看到它們已經具有可以使用的RNN對象。定義它時,有兩個基本參數:
- input_size —輸入x中預期要素的數量
- hidden_size —處于隱藏狀態h的特征數
input_size為1,因為我們一次使用每個序列的一個時間步長(例如,序列10、20、30中的10),而hidden_size為2,因為我們獲得了包含兩個值的隱藏狀態。
將n_layers參數定義為2意味著我們有一個帶有兩個隱藏層的堆疊RNN。
另外,我們還將參數batch_first定義為True。這意味著輸入和輸出中的批次尺寸排在首位(輸入和輸出不要錯)
輸入:輸入,h_0
- 形狀的輸入(seq_len,batch,input_size):包含輸入序列特征的張量。
- h_0的形狀(num_layers * num_directions,batch,hidden_size):張量,包含批次中每個元素的初始隱藏狀態。
RNN的輸入應該是形狀為1 x 3 x 1的輸入數組。該序列包含三個時間步長,分別是數據集的第一批10、20和30。從每個批次中,大小為1的輸入將作為該序列的三個時間步長被饋送到網絡三遍。
隱藏狀態h_0是我們的第一個隱藏數組,我們將其與形狀為1 x 1 x 2的第一時間步輸入一起饋入網絡。
輸出:輸出,h_n
- 形狀的輸出(seq_len,batch,num_directions * hidden_size):張量,包含每個t的RNN的最后一層的輸出特征(h_t)。
- h_n的形狀(num_layers * num_directions,batch,hidden_size):張量包含t = seq_len的隱藏狀態。
輸出包含形狀為1 x 3 x 2的每個時間步長由神經網絡計算的所有隱藏狀態,h_n是最后一個時間步長的隱藏狀態。這對于保持有用很有用,因為如果我們選擇使用堆疊式遞歸網絡,則這將是隱藏狀態,該狀態將在第一時間步進給,形狀為1 x 1 x 2。
所有這些數組都在上面的示例中表示,并且可以在RNN圖中看到。需要注意的另一件事是,使用遞歸網絡和"時間序列預測"的特定示例,將num_directions設置為2將意味著預測未來和過去。此處將不考慮這種類型的配置。
我將在實現RNN以及如何對其進行培訓的過程中留下一段代碼。我還將將其留給您使用,以根據需要與所需的數據集一起使用。在使用網絡之前,請不要忘記規范化數據并創建數據集和數據加載器。
總結思想
為了以一個簡短的總結來結束這個故事,我們首先看到了通常使用遞歸網絡解決的兩種類型的問題,即時間序列預測和自然語言處理。
后來,我們看到了一些典型配置的示例,以及一個實際示例,其目的是使用多對一配置預測未來的一步。
在前向傳遞中,我們了解了輸入和隱藏狀態如何與遞歸層的權重和偏差交互作用,以及如何使用隱藏狀態中包含的信息來預測下一個時間步長值。
反向傳遞只是鏈規則的應用,從損失梯度相對于預測的關系到相對于我們要優化的參數的變化。
最后,我們瀏覽了有關RNN的PyTorch文檔的一部分,并討論了用于構建基本循環網絡的最重要部分。
感謝您的閱讀!也許您從這個冗長的故事中得到了一些啟示。我寫它們是為了幫助我理解新概念,并希望也能幫助其他人。
原文鏈接:https://towardsdatascience.com/rnns-from-theory-to-pytorch-f0af30b610e1