[[391003]]

 前言

大家好，我是bigsai!最近，大數加減頻頻登上筆試的舞臺，小伙伴們在群里也分享自己遇到面試官碰到大數運算的題目，想著這么重要而簡單的知識點我還沒寫過，那得好好和大家一起總結一下。

群內情況

各位有過分類刷題的小伙伴，可能看到很多人分類 字符串、貪心、動態規劃、bfs、dfs、大數、數論等，初聽大數，你可能會差異：大數是個啥?聽起來怪高大上的。

大數，其實就是很大很大數字(可能遠超32、64位，基礎類型無法表示)的加減法，在Java中我們可以使用一個大數類(BigInteger等)很容易解決大數的各種運算，但如果遇到面試官他肯定會讓你手寫的。

這個數字一般用字符串、鏈表等形式表示、返回，大數運算的核心就是：模擬，模擬我們日常用紙筆算數字的加減乘除流程，然后再根據計算機、編程語言等特性適當存儲計算即可，不過，大數除法運算稍微特殊一點，和我們直接模擬的思維方式稍有不同，它就是轉換了一下成特殊的加減法運算，后面會細談。

大數加法

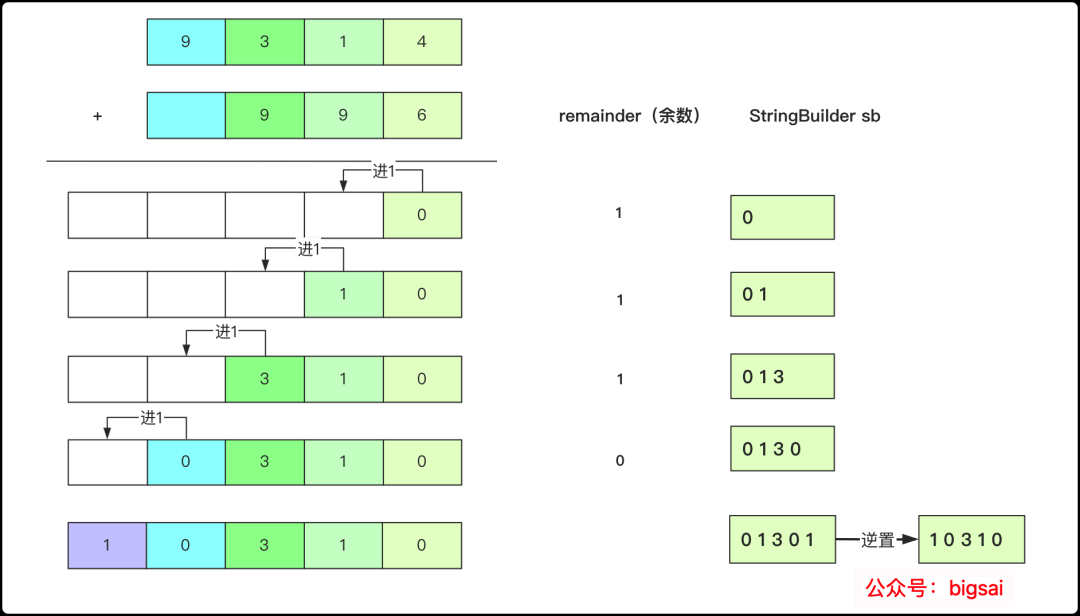
大數加法是最簡單的，簡單模擬即可。首先，我們想一下兩個數加法的流程：從右向左計算求和、進位，一直到最后。

在編程語言中同樣也是模擬從右向左逐位相加的過程，不過在具體實現上需要注意一些細節。

1、枚舉字符串將其轉換成char[]提高效率

2、從右往左進行計算，可以將結果放到一個數組中最后組成字符串，也可以使用StringBuider拼接，拼接的時候最后要逆置一下順序。

3、余數每次疊加過需要清零，兩數相加如果大于等于10即有余數，添加到結果中該位置的數也應該是該數%10的結果。

4、計算完最后還要看看余數是否為1，如果為1需要將其添加到結果，例如 "991"+"11"算三個位置為002但還有一個余數需要添加，所以應該是1002。

一個加法流程

當然在具體實現上方法較多，你可以首先就將字符串逆置然后從前往后就可以計算了。當然我這里實現的是字符串從后向前各個位對應計算，然后將結果順序添加到StringBuilder上。

這題在力扣【415兩數相加】可以檢驗自己代碼，實現代碼為：

public String addStrings(String num1, String num2) { 
// 公眾號：bigsai 歡迎你的關注 
    int len1=num1.length()-1,len2=num2.length()-1; 
    char ch1[]=num1.toCharArray(); 
    char ch2[]=num2.toCharArray(); 
 
    StringBuilder sb=new StringBuilder(); 
    int remainder =0;//計算余數 
    while (len1>=0||len2>=0) 
    { 
        int n1=len1>=0?(ch1[len1--]-'0'):0; 
        int n2=len2>=0?(ch2[len2--]-'0'):0; 
        int num=n1+n2+remainder;//求和對應數字 
        remainder=num/10;//是否進位 
        sb.append(num%10);// 添加到結果字符串中 
    } 
 
    if(remainder>0)//是否還需要進位 
    { 
        sb.append(remainder); 
    } 
    //反裝即為結果 
    return sb.reverse().toString(); 
} 

大數減法

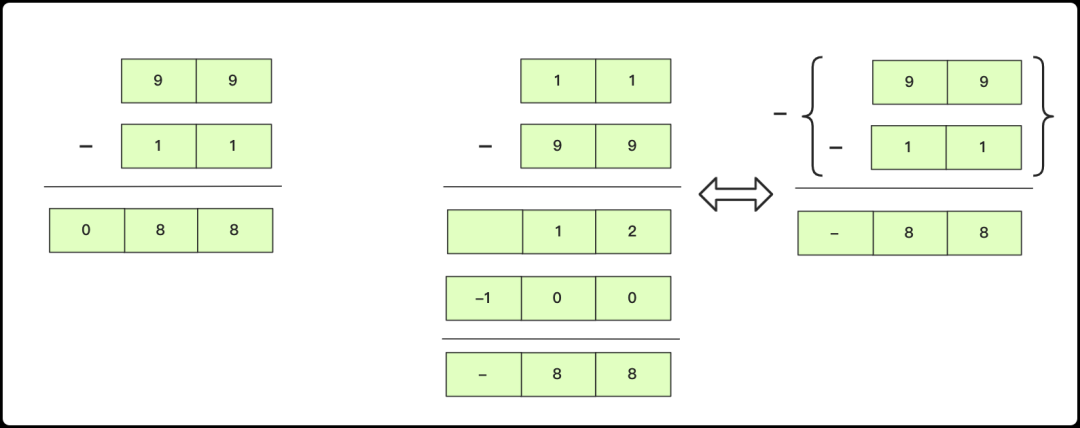
加法對應的就是減法，有了上面大數加法的實現思路，那么我想你在大數減法也應該有點想法，但是減法和加法不同的是減法有位置的區別，加法需要進位而減法需要借位。并且大整正數減法可能產生正負也不一定。

兩個正數，如果大數減去小數，那么一切正常，結果是一個正數;但如果小數減去大數，那么結果將是一個負數，并且結果處理起來比較麻煩。所以在這里全部轉成大-小處理(大-小不存在不能借位的情況)。

減法轉成大-小

1、執行計算前首先比較減數(num1)和被減數(num2)的大小，如果num1>num2,那么就模擬num1-num2的過程，如果num1

2、在比較兩個數字大小的時候，因為是字符形式，首先比較兩個字符串的長度，長的那個更大短的那個更小，如果兩個字符串等大，那么就可以通過字典序從前往后進行比較(Java可直接使用compareTo方法)。

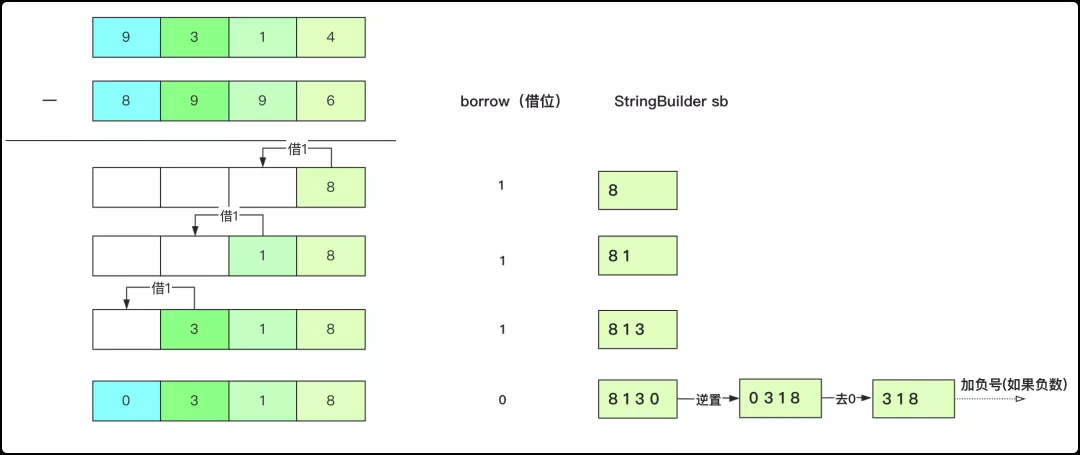
3、和加法不同的是，減法前面可能產生若干前綴0，這些0是需要你去掉的，例如"1100"-"1000"計算得到的結果為"0100",你就要把前面的0去掉返回"100"。

4、具體實現的時候和加法相似，如果使用StringBuilder存儲，需要逆置順序，如果是個負數，前面還要加上'-'.

5、每個位置正常進行減法運算，如果值小于0，那么就需要向上借位(+10),那么處理上一位進行減法時候還要將借位的處理一下。

一個減法大概流程

這題在力扣上沒有原題，但是可以在小米OJ【大數相減】上驗證自己代碼的正確性，具體實現的代碼為：

public static boolean compare(String num1,String num2) 
{ 
    if(num1.length()<num2.length()) 
        return  false; 
    else if(num1.length()>num2.length()) 
        return true; 
    else 
        return num1.compareTo(num2)>0; 
} 
public static  String subtractString(String num1,String num2) { 
    char sign='+';//正負號 
    //讓num1>num2 如果num1<num2 那么結果就是—(num2-num1)  
    //可以先將num1和num2交換和前面情況統一 
    if(!compare(num1,num2)) 
    { 
        sign='-'; 
        String team = num2; 
        num2 = num1; 
        num1 = team; 
    } 
    int len1=num1.length()-1; 
    int len2=num2.length()-1; 
 
    char ch1[] = num1.toCharArray(); 
    char ch2[] = num2.toCharArray(); 
    StringBuilder sb=new StringBuilder(); 
    int borrow=0;//借位 
    while (len1>=0||len2>=0) 
    { 
        int n1=len1>=0?(ch1[len1--]-'0'):0; 
        int n2=len2>=0?(ch2[len2--]-'0'):0; 
 
        int num=n1-n2-borrow; 
        borrow=0; 
        if(num<0)//需要向前借位 
        { 
            borrow=1; 
            num+=10; 
        } 
        sb.append(num); 
    } 
 
    sb=sb.reverse();//需要先翻轉 
    int index = 0;//去掉前面沒用的’0‘ 
    while (index<sb.length()&&sb.charAt(index) == '0') 
    { 
        index++; 
    } 
    //如果兩個數相同 直接返回"0" 
    if(index==sb.length()) 
        return "0"; 
    if(sign=='+')//如果正數  
        return  sb.substring(index); 
    else  return sign+sb.substring(index);//負數需要返回 
} 

 大數乘法

大數乘法乍一想可能比較復雜，因為乘法比起加法可能進位不光是1，還有兩個數各種位置都需要相乘計算，這時候就需要我們化繁為簡了。

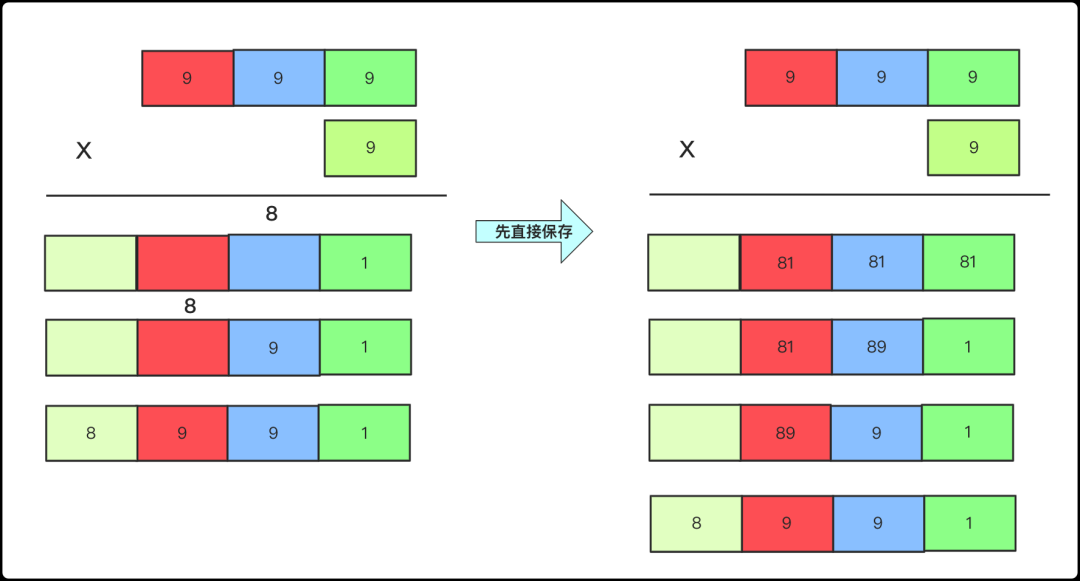
多*多考慮起來可能有些麻煩，但是如果多*一考慮起來呢?如果是多位乘以一位數，那么就拿一位的分別乘以多位數的個位、十位、百位，在計算的同時考慮一下進位的情況。

但是也可以先直接用int類型數組存儲各位的乘積然后從右向左進行進位，如下圖所示。

先計算后進位

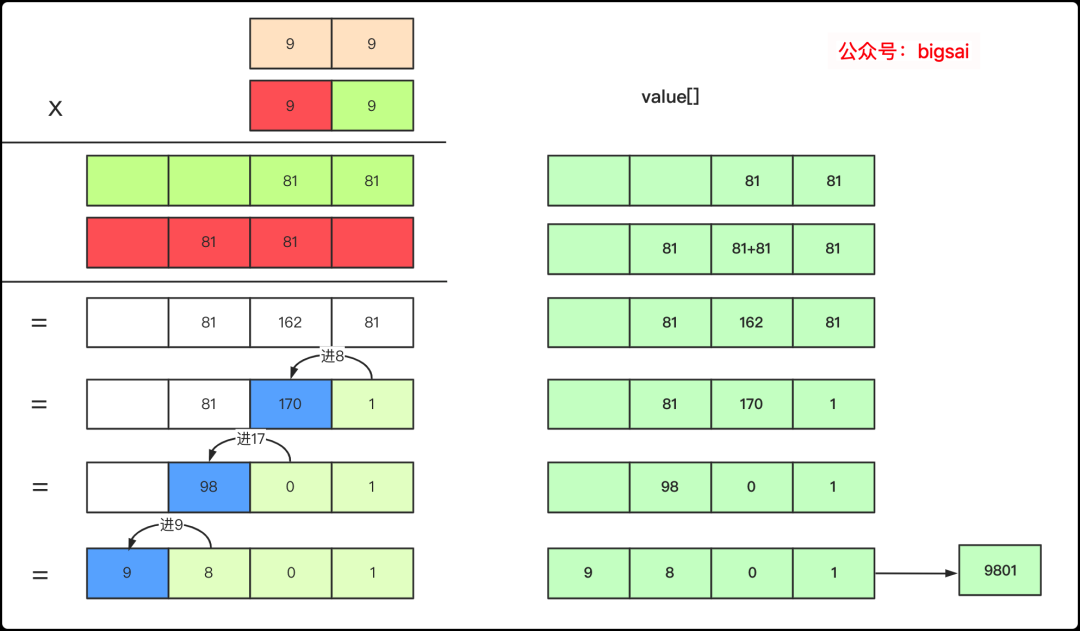
而多*多 也是這個道理，將不同位乘積先疊加到對應位置上，然后從右向左進位，一直到不需要進位為止。

一個乘法流程

你可能會疑問，如果兩個數組的長度分別為a和b這個數組到底該開多大呢?

• a+b大小就夠了，怎么分析呢?其中一個a不變。另一個b變成最小b+1數字即十的倍數，那么這樣在相乘的時候也不過是a+b長度，所以這里a+b長度就夠了。

這題有力扣對應題可以去試試【43字符串相乘】，具體代碼為：

public String multiply(String num1, String num2) { 
    if("0".equals(num1)||"0".equals(num2))return "0"; 
    char a[]=num1.toCharArray(); 
    char b[]=num2.toCharArray(); 
 
    int value[]=new int[a.length+b.length]; 
 
    for(int i=a.length-1;i>=0;i--) 
    { 
        for(int j=b.length-1;j>=0;j--) 
        { 
            int index=a.length-1-i+b.length-1-j; 
            value[index]+=(a[i]-'0')*(b[j]-'0'); 
        } 
    } 
    for(int i=0;i<value.length-1;i++) 
    { 
        value[i+1]+=value[i]/10; 
        value[i]=value[i]%10; 
    } 
    int index=value.length-1; 
    while(value[index]==0) 
    {index--;} 
    StringBuilder sBuilder=new StringBuilder(); 
    while (index>=0) { 
        sBuilder.append(value[index--]); 
    } 
    return sBuilder.toString(); 
} 

大數除法

大數加減乘都搞定了，通過模擬來實現，但是大數除法也通過模擬來實現?

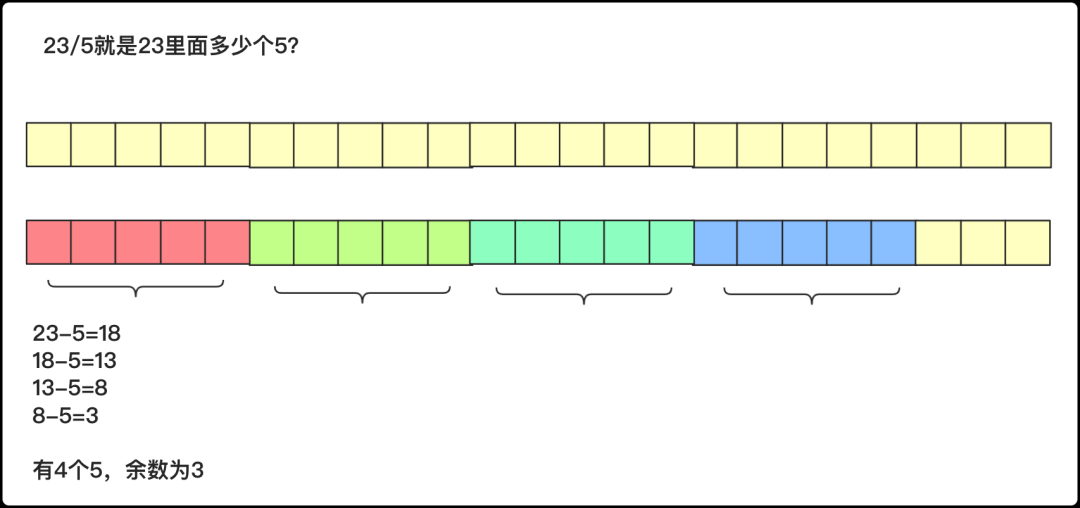
并不是，對于大數a/b，一般最多要求求到其整數解或者余數，即a/b=c……d(a,b,c,d均為整);也就是a里面有c個b，并且還剩下d。核心是先求c是多少，對于程序來說，可以通過枚舉啊，將除法變成減法，從a中不斷減d，一直到不能減為止。

除法轉成減法運算

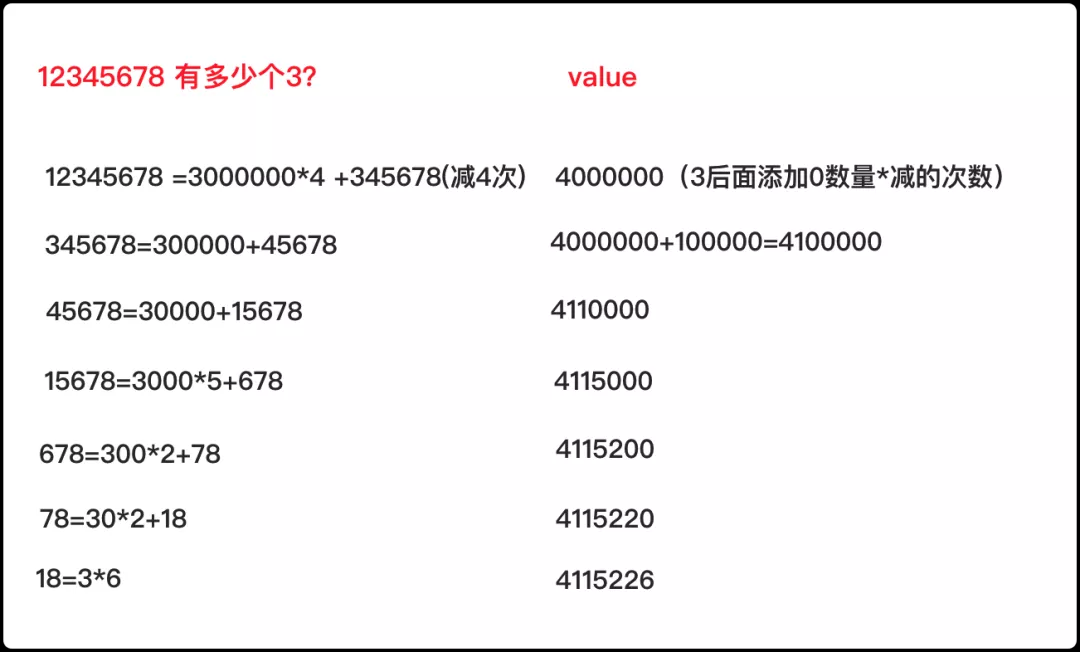
但是有個問題，如果被除數a很大很大，可能有居多個b，那么這樣時間復雜度太高了，不可能執行那么多次，那么需要怎么樣去優化這個方法呢?

那就要加速尋找次數，減少這個減法的次數了，減法次數減小的一個最好方案就是能不能擴大除數b。如果b后面加個'0'，那么算出來的結果就乘以10，減法的次數變成原來十分之一。根據這個思想我們可以一直每次找到b的最大10的倍數(小于a)計算減的次數再換算成減b的總詞數，將結果要以字符串方式保留，后面一直迭代到最后為止,這雖然是一道除法運算的題，但是也蘊含減法和加法(次數疊加到結果中)。

計算思想

當然，也有一些人使用二分法來壓縮尋找可以被減的次數也是可以的(加法可以迭代數字實現二分倍數)，具體實現的話也不是很困難，但是代碼量可能比較多所以一般的面試筆試不會讓你現場寫的，所以好好掌握前面的減法、減法、乘法的代碼即可。

當然，如果你依然很想看大數除法部分的代碼，可以百度搜一下或者在文末評論催更一下，如果有感興趣的可以后面把代碼補充上。

結語

到這里，大數的加減乘除基本都講解完啦，不知道你有沒有收獲，因為這里的大數都是用字符串的方式存儲和處理，遇到的最多，但是也可能遇到一些鏈表、數組等其他形式存儲的需要處理，但是整體的思想都是一樣的。