[[404279]]

前言

大家好，我是bigsai。

拓撲排序，很多人都可能聽說但是不了解的一種算法。不知者大多會提出這樣的疑問：

這是某種排序算法?這好像是一種圖論算法?圖也能排序?

非線性結構在傳統(tǒng)意義上確實不太好排序，而拓撲排序它是對有向圖的頂點排成一個線性序列。并且不一定唯一。

什么是拓撲排序?

對一個有向無環(huán)圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意一對頂點u和v，若邊∈E(G)，則u在線性序列中出現(xiàn)在v之前。通常，這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列，簡稱拓撲序列。簡單的說，由某個集合上的一個偏序得到該集合上的一個全序，這個操作稱之為拓撲排序。

拓撲排序有何作用?

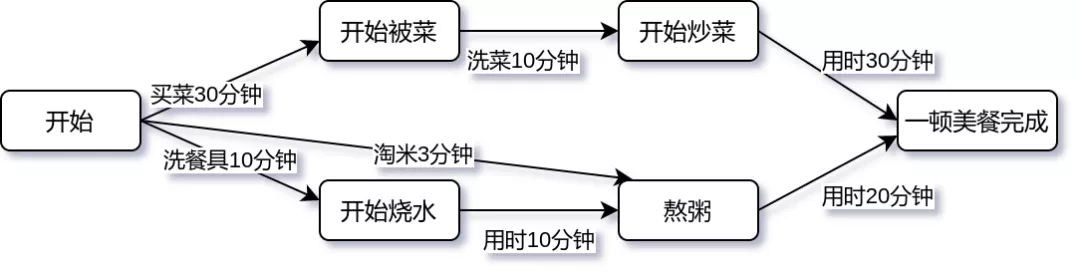
拓撲排序的應用其實還是蠻多的，拓撲排序在一些工程有多道工序時候可以獲取一個有效的加工順序、還有些游戲里的任務成就必須滿足一個符合的拓撲排序才能解鎖下一關、還有一些項目或者環(huán)境的依賴關系集……

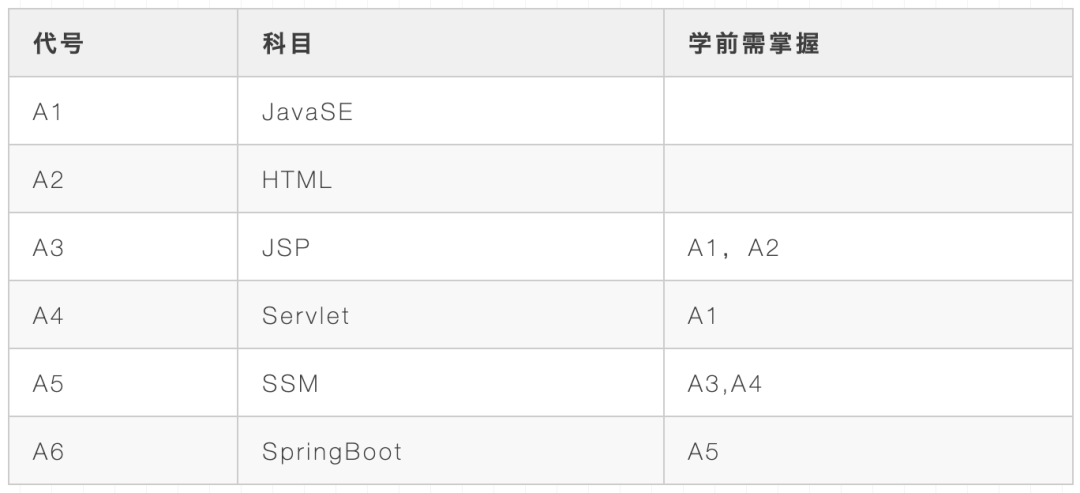
當然上面的例子可能不夠具體，離我們稍微近一點的就是課程學習上，比如你學習數(shù)據(jù)結構之前基本要學習C或者C++這門課，因為數(shù)據(jù)結構中需要懂和會用C++的代碼;學習操作系統(tǒng)、計算機網(wǎng)絡之前要學習數(shù)據(jù)結構這門課，因為里面涉及到很多數(shù)據(jù)結構和算法;學習Java Web開發(fā)前要學習JavaSE和HTML這兩門課;不同院校課程安排截然不同但均能很好的連接起來，就是因為安排的課程滿足一個拓撲排序。

拓撲排序還是不能理解?我舉個更詳細的例子，學習Java系列的教程部分，可能有下面這個順序：

就比如學習Java系類(部分)從Java基礎，到JSP/Servlet，到SSM，到SpringBoot，SpringCloud等是個循序漸進、且有前提依賴的過程。在JSP學習要首先掌握Java基礎和HTML基礎。學習框架要掌握JSP/Servlet和JDBC之類才行。那么，這個學習過程即構成一個拓撲序列。當然這個序列也不唯一，你可以對不關聯(lián)的學科隨意選擇順序(比如Html和Java可以隨便先開始哪一個)。

那上述序列可以簡單表示為：

這五種均為可以選擇的學習方案，對課程安排可以有參考作用，這五個都是上面有向無環(huán)圖(DAG)的拓撲序列，只是小的選擇的策略不同(先學Java或者先學HTML不要緊，但是要滿足整個順序要求)，不影響滿足規(guī)則順序!

對于拓撲排序，還有一些比較專業(yè)的名詞需要銘記：

DAG：有向無環(huán)圖

AOV網(wǎng)：數(shù)據(jù)在頂點，頂點表示活動，邊表示活動的先后關系，可以理解為一種面向對象。

AOE網(wǎng)：數(shù)據(jù)在邊上，頂點表示事件，有向邊表示活動，邊上的權值表示該活動持續(xù)的時間，可以理解為面向過程。

很多人不知道AOE網(wǎng)干啥用的，拓撲排序是解決一個工程能否順序進行的問題，但有時還需解決工程完成需要的最短時間。而AOE經(jīng)常使用在求關鍵路徑中(這里就先不進行詳細介紹內容和算法了),圖片來源https://www.cnblogs.com/svod5306/p/14723338.html)。

我們今天講的拓撲排序就是在AOV中找到不破壞圖結構的序列，對于有向無環(huán)圖，需要注意一下圖中：若A在B前面，則不存在B在A前面的路徑(不能成環(huán))。圖中兩個相鄰節(jié)點在拓撲序列中只需要滿足前后關系而不一定需要相鄰(節(jié)點只需滿足相對的前后關系，所以拓撲排序并不一定唯一)。

算法分析

上面簡單的介紹了拓撲排序，下面詳細講講拓撲排序的求法。

正常步驟為(方法不一定唯一)：

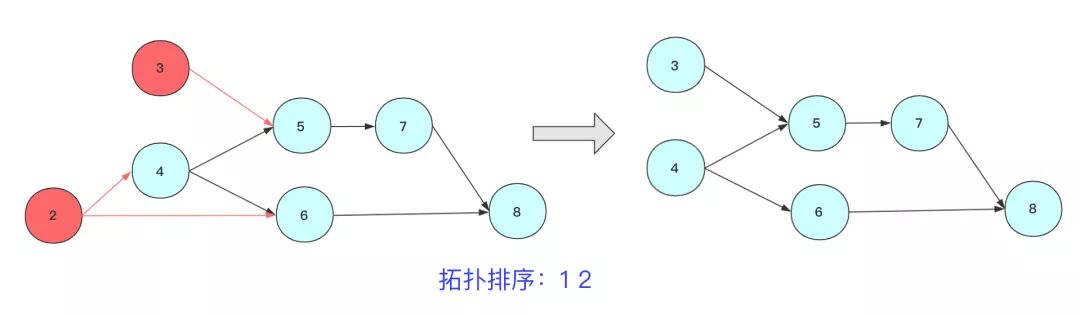
1.從DAG圖中找到一個沒有前驅的頂點輸出。可以遍歷入度為0的節(jié)點，也可以用優(yōu)先隊列維護。

2.刪除以這個點為起點的邊。刪除一條邊，其指向節(jié)點的入度減1，這樣為了找到下個沒有前驅節(jié)點的頂點。

3.重復上述，直到最后一個頂點被輸出。如果還有頂點未被輸出，則說明有環(huán)!

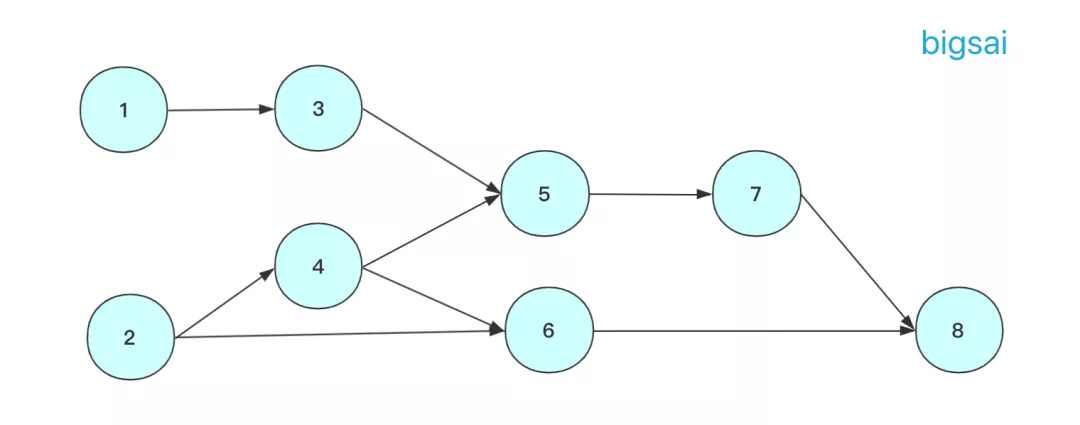
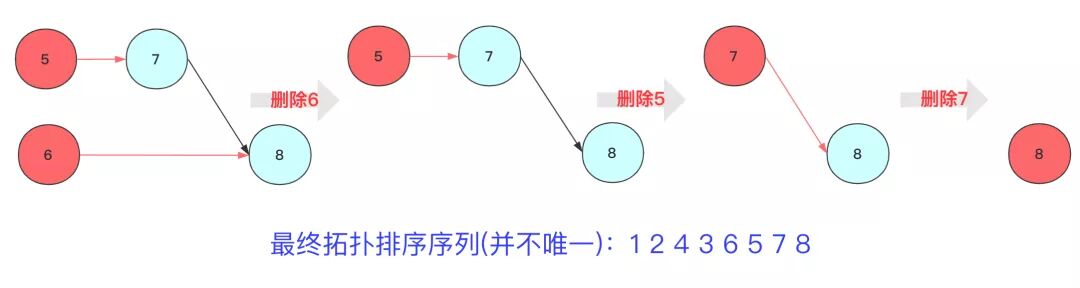
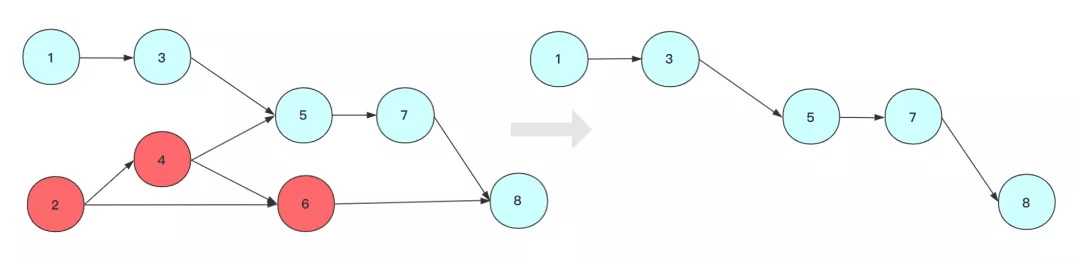
對于上圖的簡單序列，可以簡單描述步驟為：

step1：刪除節(jié)點1(或者2)及其指向的邊，將節(jié)點輸出

step2：刪除節(jié)點2(或者3)及其指向的邊，將節(jié)點輸出

step2(這里進行兩步)：刪除節(jié)點3(或者4)及其指向的邊，將節(jié)點輸出，緊接著刪除節(jié)點3(或者6)其指向的邊，將節(jié)點輸出。

step3：按照上述規(guī)則重復進行，直到所有節(jié)點都被刪除。

這樣就完成一次拓撲排序流程，得到一個拓撲序列，但是這個序列并不唯一，從算法執(zhí)行過程中也看到有很多選擇方案，具體得到結果看你算法的設計了，但只要滿足DAG圖中前后相對關系。

另外觀察 1 2 4 3 6 5 7 8 這個序列滿足我們所說的有關系的節(jié)點指向的在前面，被指向的在后面。如果完全沒關系那不一定前后(例如1,2)

代碼實現(xiàn)

對于拓撲排序，如何用代碼實現(xiàn)呢?

雖然在上面詳細介紹了思路和流程，也很通俗易懂，但是實際上代碼的實現(xiàn)還是很需要斟酌的，如何在空間和時間上能夠得到較好的平衡且取得較好的效率?

首先要考慮存儲，對于節(jié)點，是用鄰接矩陣還是鄰接表存儲呢，通常拓撲排序如果使用矩陣存儲都是比較稀疏的，比較浪費內存空間，這里還是使用鄰接表來存儲節(jié)點。

另外，如果圖中節(jié)點是1，2，3，4，5，6這樣的有序編號，我們可以直接用數(shù)組，但是如果遇到1，2，88，9999類似不連續(xù)跨度很大編號節(jié)點，也可以考慮用Map存儲映射一下位置。

那么我們具體的代碼思想為：

①新建node類，包含節(jié)點數(shù)值和它的指向節(jié)點集合(這里直接用List集合)

②初始化一個人node數(shù)組，輸入/枚舉節(jié)點之間關系，被指向的節(jié)點入度+1!(例如A—>C)那么C的入度+1;

③掃描所有node(這里掃描數(shù)組)。將所有入度為0的點加入一個容器棧(隊列)中。

④當棧(隊列)不空的時候，拋出其中任意一個node(只要入度為零可以隨便選擇順序)。將node輸出，并且node指向的所有節(jié)點入度減1。如果某個點的入度被減為0，那么就將它加入棧(隊列)。

⑤重復上述操作，直到棧(隊列)為空。

這里主要是利用棧或者隊列儲存入度只為0的節(jié)點，只需要初次掃描表將入度為0的放入棧(隊列)中。

因為節(jié)點之間是有相關性的，一個節(jié)點若想入度為零，那么它的前驅節(jié)點點肯定在它前入度為0，拆除關聯(lián)箭頭將自己入度減1，在一個有向無環(huán)圖中總會有大于等于1個入度為0的節(jié)點。

在具體實現(xiàn)上，方式是有多樣的，我的這個只是一個簡單的演示，效率不一定很高，大家參考一下即可。

具體實現(xiàn)代碼為：

import java.util.ArrayDeque; 
import java.util.ArrayList; 
import java.util.List; 
import java.util.Queue; 
import java.util.Stack; 
 
public class tuopu { 
    static class node 
    { 
        int value; 
        List<Integer> next; 
        public node(int value) { 
            this.value=value; 
            next=new ArrayList<Integer>(); 
        } 
        public void setnext(List<Integer>list) { 
            this.next=list; 
        } 
    } 
 
    public static void main(String[] args) { 
        // TODO Auto-generated method stub 
        node []nodes=new node[9];//儲存節(jié)點 
        int a[]=new int[9];//儲存入度 
        List<Integer>list[]=new ArrayList[10];//臨時空間，為了存儲指向的集合 
        for(int i=1;i<9;i++) 
        { 
            nodes[i]=new node(i); 
            list[i]=new ArrayList<Integer>(); 
        } 
        initmap(nodes,list,a); 
 
        //主要流程 
        //Queue<node>q1=new ArrayDeque<node>(); 
        Stack<node>s1=new Stack<node>(); 
        for(int i=1;i<9;i++) 
        { 
            //System.out.print(nodes[i].next.size()+" 55 "); 
            //System.out.println(a[i]); 
            if(a[i]==0) {s1.add(nodes[i]);} 
 
        } 
        while(!s1.isEmpty()) 
        { 
            node n1=s1.pop();//拋出輸出 
            System.out.print(n1.value+" "); 
            List<Integer>next=n1.next; 
            for(int i=0;i<next.size();i++) 
            { 
                a[next.get(i)]--;//入度減一 
                if(a[next.get(i)]==0)//如果入度為0 
                { 
                    s1.add(nodes[next.get(i)]); 
                } 
            } 
        } 
    } 
 
    private static void initmap(node[] nodes, List<Integer>[] list, int[] a) { 
        list[1].add(3); 
        nodes[1].setnext(list[1]); 
        a[3]++; 
        list[2].add(4);list[2].add(6); 
        nodes[2].setnext(list[2]); 
        a[4]++;a[6]++; 
        list[3].add(5); 
        nodes[3].setnext(list[3]); 
        a[5]++; 
        list[4].add(5);list[4].add(6); 
        nodes[4].setnext(list[4]); 
        a[5]++;a[6]++; 
        list[5].add(7); 
        nodes[5].setnext(list[5]); 
        a[7]++; 
        list[6].add(8); 
        nodes[6].setnext(list[6]); 
        a[8]++; 
        list[7].add(8); 
        nodes[7].setnext(list[7]); 
        a[8]++; 
 
    } 
} 

輸出結果

2 4 6 1 3 5 7 8 

當然，上面說過用棧和隊列都可以!如果使用隊列就會得到1 2 3 4 5 6 7 8 的拓撲序列

至于圖的構造，因為沒有條件可能效率并不高，算法也可能不太完美，如有優(yōu)化錯誤還請大佬指正!

拓撲排序找環(huán)

前面說到，拓撲排序需要在有向無環(huán)圖中才能得到一個拓撲序列，但是如果給定一個有向圖，怎么知道它是否可以形成一個拓撲序列呢?

當然是在拓撲排序算法上進行改動，我們在進行拓撲排序會刪除所有入度為0的節(jié)點，但是如有有環(huán)那么刪除節(jié)點個數(shù)就小于所有節(jié)點個數(shù)，在具體實現(xiàn)上，我們只需要在棧或者隊列拋出時候通過一個計數(shù)器統(tǒng)計數(shù)字即可。

當然這個問題力扣207有原題可以看看自己代碼是否能夠ac，問題描述：

• 你這個學期必須選修 numCourses 門課程，記為 0 到 numCourses - 1 。
• 在選修某些課程之前需要一些先修課程。先修課程按數(shù)組 prerequisites 給出，其中 prerequisites[i] = [ai, bi] ，表示如果要學習課程 ai 則 必須 先學習課程 bi 。
• 例如，先修課程對 [0, 1] 表示：想要學習課程 0 ，你需要先完成課程 1 。

請你判斷是否可能完成所有課程的學習?如果可以，返回 true ;否則，返回 false 。

分析上面已經(jīng)給出，不過在具體實現(xiàn)代碼的時候比較靈活，不一定非得創(chuàng)建node類，思路上理的清即可。

實現(xiàn)代碼：

class Solution { 
    public boolean canFinish(int numCourses, int[][] prerequisites) { 
        int indegree[]=new int[numCourses]; 
        List<Integer> next[]=new ArrayList[numCourses]; 
 
        for(int i=0;i<numCourses;i++){ 
            next[i]=new ArrayList(); 
        } 
        for(int i=0;i<prerequisites.length;i++) { 
            int preid=prerequisites[i][1]; 
            int courseid=prerequisites[i][0]; 
            indegree[courseid]++;//入度加一 
            next[preid].add(courseid);//next指向 
        } 
        Queue<Integer>queue=new ArrayDeque<>(); 
        for(int i=0;i<numCourses;i++) {//加入入度為0的節(jié)點 
            if(indegree[i]==0){ 
                queue.add(i); 
            } 
        } 
        int nodeNum=0;//判斷刪除節(jié)點數(shù)量 入度為0刪除 如果刪除所有那么返回true 
        while (!queue.isEmpty()) 
        { 
            nodeNum++; 
            int nodeId=queue.poll(); 
            for(int i=0;i<next[nodeId].size();i++) 
            { 
                int nodeIndex=next[nodeId].get(i); 
                indegree[nodeIndex]--; 
                if(indegree[nodeIndex]==0) { 
                    queue.add(nodeIndex); 
                } 
            } 
        } 
        if(nodeNum==numCourses) 
            return true; 
        return false; 
    } 
} 

 好了，到這里拓撲排序內容講解完畢，謝謝!