尋找旋轉數組中的最小數字
本文轉載自微信公眾號「神奇的程序員K」,作者神奇的程序員K。轉載本文請聯系神奇的程序員K公眾號。
前言
把一個數組最開始的若干個元素搬到數組的末尾,就稱之為數組的旋轉。有一個遞增排序數組,將其開頭的若干個元素移動至數組的末尾,尋找其中的最小值。
本文就跟大家分享下如何用最快的速度找到遞增旋轉數組中的最小值,歡迎各位感興趣的開發者閱讀本文。
實現思路
乍一看這個問題,一部分開發者首先想到的解法就是從頭到尾遍歷下數組,這樣就能找出最小的元素。這種思路的時間復雜度是O(n),沒有將題目中的條件利用起來,因此這種方案不是本題的正確答案。
舉例分析
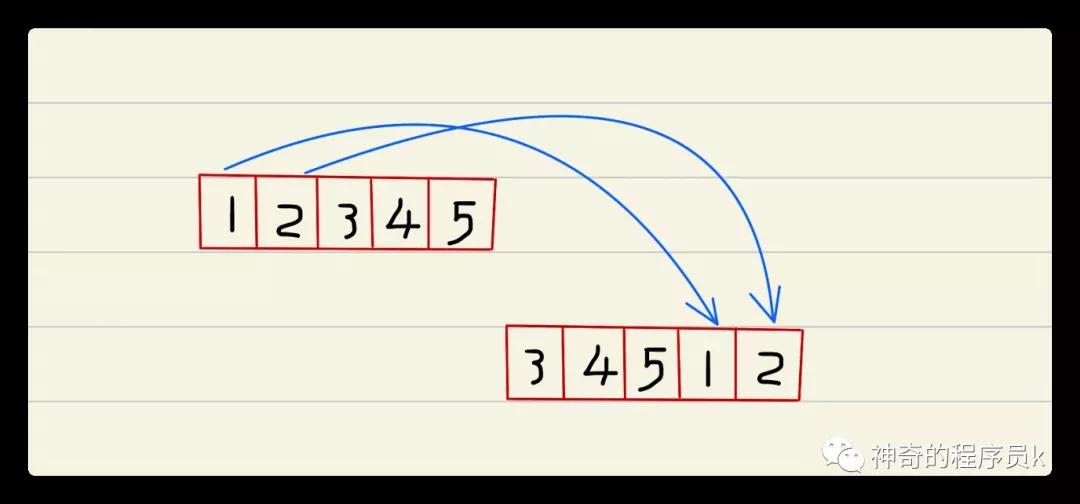
接下來,我們來分析下題目,通過舉例、觀察來尋找突破口。我們先來列舉一個遞增數組。
如上圖所示,我們準備了一個1 ~ 5的遞增數組,然后將其開頭的兩個元素搬到了數組的末尾,這樣就構成了一個旋轉數組。
經過一番觀察后,我們可以發現:
- 旋轉后的數組可以劃分為兩個已經排序的小數組
- 前面子數組的元素都大于等于后面子數組的元素
- 最小的數字是這兩個子數組的分界線
二分查找
經過上面的分析,我們可知旋轉后的數組在一定程度上是排好序的,因此我們可以嘗試使用二分查找的思路來尋找最小的元素。
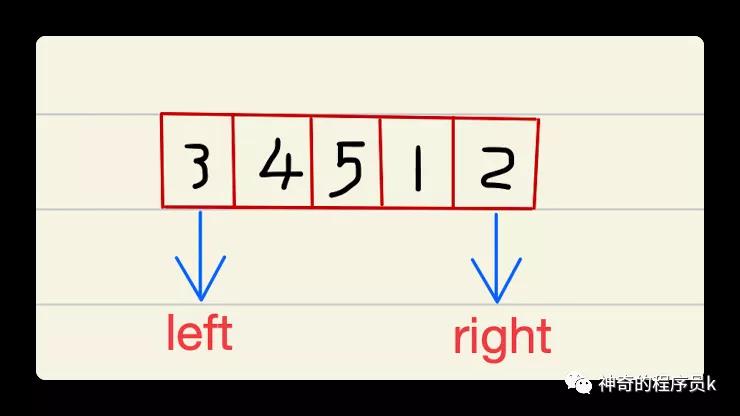
接下來,我們準備兩個指針(左指針、右指針),左指針指向數組的第一個元素,右指針指向數組的末尾元素,如下圖所示:
觀察上圖后,我們發現它們的中間元素是5、最小值在5的后面,因此我們就可以排除中間值之前的元素了,移動左指針至5,如下圖所示:
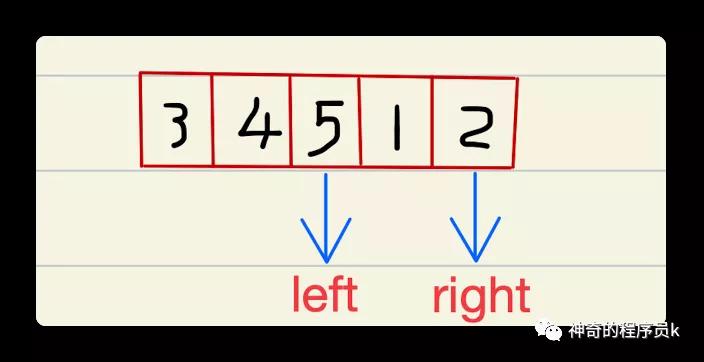
此時,它們的中間元素是1,我們發現最小值2的前面,因此我們就可以將右指針移動至中間1,如下所所示:圖片
最后,我們發現左指針與右指針相鄰,右指針指向的元素正好是旋轉數組的最小元素。
經過上述畫圖分析后,我們可以得到如下規律:
- 如果兩個指針的中間元素大于等于左指針指向的元素,那么最小值一定在中間元素的后面,移動左指針至中間值位置縮小查找范圍
- 如果兩個指針的中間元素小于等于右指針指向的元素,那么最小值一定在中間元素的前面,移動右指針至中間值位置縮小查找范圍
- 左指針一定指向前面的遞增子數組,右指針一定指向后面的遞增子數組
- 當左、右指針相鄰時,右指針所指向的元素就是這個數組的最小值
時間復雜度分析:每次移動指針,查找范圍都會縮小到原先的一半,因此總的時間復雜度為O(logn)
特殊情況
上述規律可以滿足大多數情況,當出現下述情況時我們就不能采用二分查找了:
- 當數組的0號元素小于最后一個元素時,證明這個數組是排好序的,它的最小值是數組的第0號元素
- 當左指針與右指針指向的元素相同且它們的中間元素也與其相同,那么就只能使用順序查找,如下圖所示:
實現代碼
接下來,我們根據上述所講內容來總結下思路:
- 判斷數組是否已經排好序(第一個元素是否小于最后一個元素)
- 左指針指向的值大于等于右指針指向的值就根據條件移動左、右指針:
- 循環終止條件:左指針與右指針相鄰
- 求左、右指針的中間索引
- 左指針指向的值與右指針指向的值相同且中間元素也與之相同(使用順序查找 )
- 中間值大于等于左指針指向的值,移動左指針位置至中間值位置
- 中間值小于等于右指針指向的值,移動右指針位置至中間值位置
- 循環結束,返回最小值
代碼如下所示:
- // 把一個數組最開始的若干個元素搬到數組的末尾,我們稱之為數組的旋轉。
- // 輸入一個遞增排序的數組的一個旋轉,輸出旋轉數組的最小元素。
- // 例如,數組[3,4,5,1,2]為[1,2,3,4,5]的一個旋轉,該數組的最小值為1。
- export default class FindWhirlingArrayMinVal {
- private leftPointer;
- private rightPointer;
- private middleIndex;
- constructor() {
- this.leftPointer = 0;
- this.rightPointer = 0;
- this.middleIndex = 0;
- }
- public getMinValue(incrementArray: Array<number>): number {
- this.rightPointer = incrementArray.length - 1;
- // 第一個元素小于最后一個元素,證明數組是排好序的
- if (incrementArray[this.leftPointer] < incrementArray[this.rightPointer]) {
- // 其最小值為第一個元素
- return incrementArray[this.leftPointer];
- }
- while (
- incrementArray[this.leftPointer] >= incrementArray[this.rightPointer]
- ) {
- // 循環終止條件: 右指針與左指針相鄰,最小值為右指針所指向的值
- if (this.rightPointer - this.leftPointer === 1) {
- this.middleIndex = this.rightPointer;
- break;
- }
- // 求中間值
- this.middleIndex = Math.floor((this.leftPointer + this.rightPointer) / 2);
- // 左指針指向的值與右指針指向的值相同且中間元素也與之相同
- // 則無法使用二分查找,需要順序查找
- if (
- incrementArray[this.leftPointer] ===
- incrementArray[this.rightPointer] &&
- incrementArray[this.middleIndex] === incrementArray[this.leftPointer]
- ) {
- // 按順序查找
- let minValue = incrementArray[0];
- for (let i = 0; i < incrementArray.length; i++) {
- if (incrementArray[i] < minValue) {
- minValue = incrementArray[i];
- }
- }
- return minValue;
- }
- if (
- incrementArray[this.middleIndex] >= incrementArray[this.leftPointer]
- ) {
- // 中間值大于等于左指針指向的值
- // 移動左指針至中間值位置
- this.leftPointer = this.middleIndex;
- } else if (
- incrementArray[this.middleIndex] <= incrementArray[this.rightPointer]
- ) {
- // 中間值小于等于右指針指向的值
- // 移動右指針至中間值位置
- this.rightPointer = this.middleIndex;
- }
- }
- // 循環結束,返回最小值
- return incrementArray[this.middleIndex];
- }
- }
完整代碼請移步:findWhirlingArrayMinVal-test.ts