[[411439]]

DeepMind 提出的 Rainbow 算法，可以讓 AI 玩 Atari 游戲的水平提升一大截，但該算法計算成本非常高，一個主要原因是學(xué)術(shù)研究發(fā)布的標(biāo)準(zhǔn)通常是需要在大型基準(zhǔn)測試上評估新算法。來自谷歌的研究者通過添加和移除不同組件，在有限的計算預(yù)算、中小型環(huán)境下，以小規(guī)模實驗得到與 Rainbow 算法一致的結(jié)果。

人們普遍認(rèn)為，將傳統(tǒng)強化學(xué)習(xí)與深度神經(jīng)網(wǎng)絡(luò)結(jié)合的深度強化學(xué)習(xí)，始于 DQN 算法的開創(chuàng)性發(fā)布。DQN 的論文展示了這種組合的巨大潛力，表明它可以產(chǎn)生玩 Atari 2600 游戲的有效智能體。之后有多種方法改進了原始 DQN，而 Rainbow 算法結(jié)合了許多最新進展，在 ALE 基準(zhǔn)測試上實現(xiàn)了 SOTA 的性能。然而這一進展帶來了非常高的計算成本，擁有充足計算資源的和沒有計算資源之間的差距被進一步拉大。

在 ICML 2021 的一篇論文《Revisiting Rainbow: Promoting more Insightful and Inclusive Deep Reinforcement Learning Research》中，研究者首先討論了與 Rainbow 算法相關(guān)的計算成本。研究者探討了通過結(jié)合多種算法組件，以小規(guī)模實驗得到與 Rainbow 算法一致的結(jié)果，并將該想法進一步推廣到在較小的計算預(yù)算上進行的研究如何提供有價值的科學(xué)見解。

論文地址：https://arxiv.org/abs/2011.14826

Rainbow 計算成本高的一個主要原因是學(xué)術(shù)研究發(fā)布的標(biāo)準(zhǔn)通常是需要在大型基準(zhǔn)測試（例如 ALE，其中包含 57 款強化學(xué)習(xí)智能體能夠?qū)W會玩 Atari 2600 游戲）上評估新算法。通常使用 Tesla P100 GPU 訓(xùn)練模型學(xué)會玩一個游戲大約需要五天時間。此外，如果想要建立有意義的置信邊界，通常至少執(zhí)行 5 次運行。

因此，在全套 57 款游戲上訓(xùn)練 Rainbow 需要大約 34,200 個 GPU hour（約 1425 天）才能提供令人信服的性能實驗數(shù)據(jù)。這樣的實驗只有能夠在多個 GPU 上并行訓(xùn)練時才可行，這使得較小的研究小組望而卻步。

Rainbow 算法

與原始 Rainbow 算法的論文一樣，在 ICML 2021 的這篇論文中，研究者評估了在原始 DQN 算法中添加以下組件的效果：雙 Q 學(xué)習(xí)（double Q-learning）、優(yōu)先經(jīng)驗回放（prioritized experience replay，PER）、競爭網(wǎng)絡(luò)、多步學(xué)習(xí)、分布式強化學(xué)習(xí)和嘈雜網(wǎng)絡(luò)。

該研究在四個經(jīng)典控制環(huán)境中進行評估。需要注意的是，相比于 ALE 游戲需要 5 天，這些環(huán)境在 10-20 分鐘內(nèi)就可以完成完全訓(xùn)練：

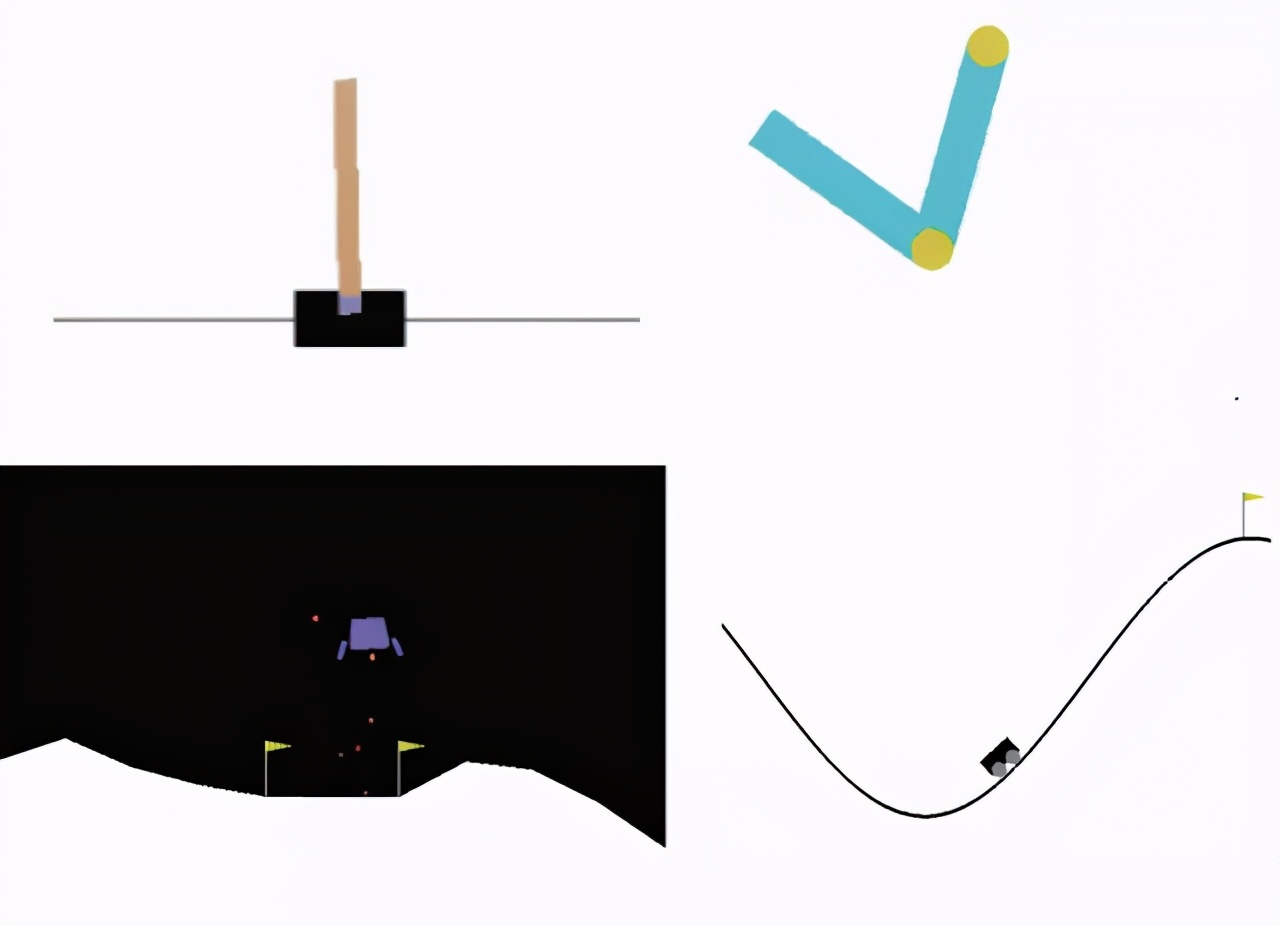
左上：在 CartPole 中，游戲任務(wù)是智能體通過左右移動平衡推車上的一根桿子；右上：在 Acrobot 中，有兩個杠桿和兩個連接點，智能體需要向兩個杠桿之間的連接點施加力以抬高下面的杠桿使其高于某個高度要求。左下：在 LunarLander 中，智能體的任務(wù)是將飛船降落在兩個旗幟之間；右下：在 MountainCar 中，智能體需要在兩座山丘之間借助一定的動力將車開到右邊的山頂。

研究者探究了將每個組件單獨添加到 DQN 以及從完整 Rainbow 算法中刪除每個組件的效果，并發(fā)現(xiàn)總的來說每一個算法組件的添加都確實改進了基礎(chǔ) DQN 的學(xué)習(xí)效果。然而，該研究也發(fā)現(xiàn)了一些重要的差異，例如通常被認(rèn)為能起到改進作用的分布式 RL 自身并不總是能夠產(chǎn)生改進。實際上，與 Rainbow 論文中的 ALE 結(jié)果相反，在經(jīng)典控制環(huán)境中，分布式 RL 僅在與其他組件結(jié)合時才會產(chǎn)生改進。

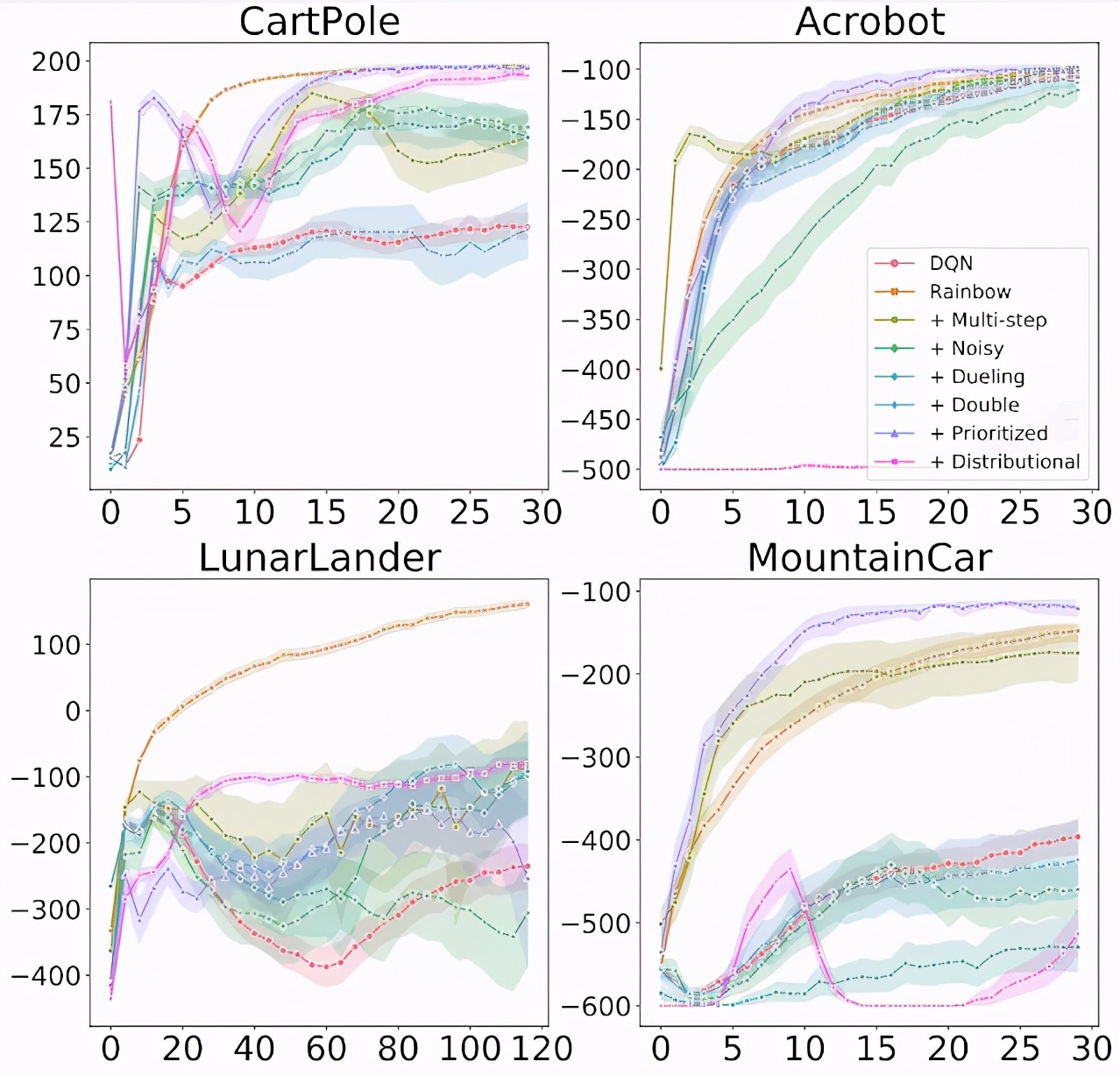
上圖顯示了在 4 個經(jīng)典控制環(huán)境中，向 DQN 添加不同組件時的訓(xùn)練進度。x 軸為訓(xùn)練 step，y 軸為性能（越高越好）。

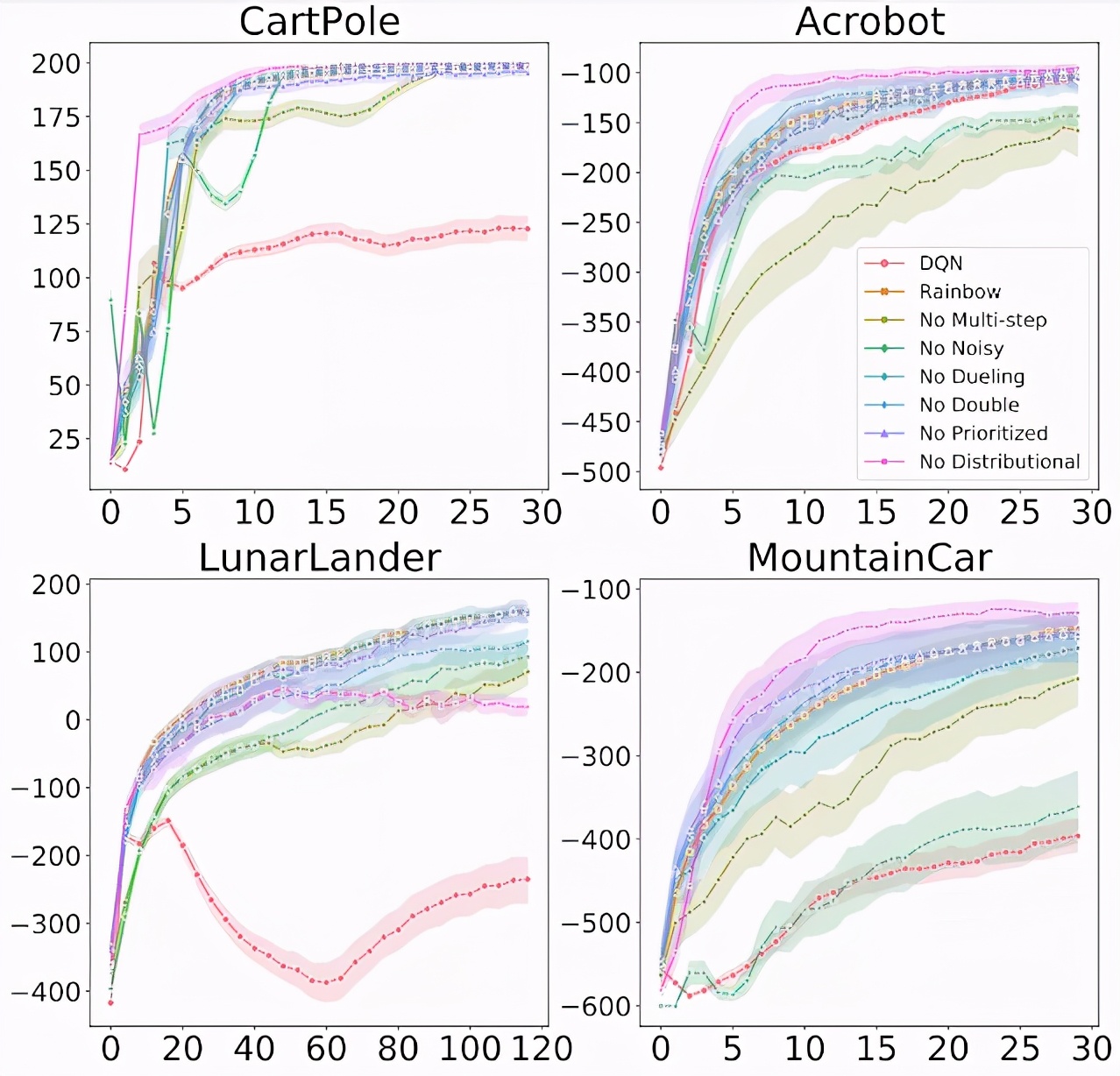
上圖顯示了在 4 個經(jīng)典控制環(huán)境中，從 Rainbow 中移除各種組件時的訓(xùn)練進度。x 軸為訓(xùn)練 step，y 軸為性能（越高越好）。

研究者還在 MinAtar 環(huán)境中重新運行了 Rainbow 實驗，MinAtar 環(huán)境由一組五個小型化的 Atari 游戲組成，實驗結(jié)果與原 Rainbow 論文類似。MinAtar 游戲的訓(xùn)練速度大約是常規(guī) Atari 2600 游戲的 10 倍，其中后者的訓(xùn)練速度是在最初的 Rainbow 算法上評估的。此外，該研究的實驗結(jié)果還有一些有趣的方面，例如游戲動態(tài)和給智能體添加基于像素的輸入。因此，該研究提供了一個具有挑戰(zhàn)性的中級環(huán)境，介于經(jīng)典控制和完整的 Atari 2600 游戲之間。

綜合來看，研究者發(fā)現(xiàn)現(xiàn)在的結(jié)果與原始 Rainbow 論文的結(jié)果一致——每個算法組件產(chǎn)生的影響可能因環(huán)境而異。研究者建議使用單一智能體來平衡不同算法組件之間的權(quán)衡，該研究的 Rainbow 版本可能與原始版本高度一致，這是因為將所有組件組合在一起會產(chǎn)生整體性能更好的智能體。然而，在不同算法組件之間，有一些重要的細(xì)節(jié)變化值得進行更徹底的探究。

「優(yōu)化器 - 損失函數(shù)」不同組合實驗

DQN 被提出時，同時采用了 Huber 損失和 RMSProp 優(yōu)化器。對于研究者而言，在構(gòu)建 DQN 時使用相同的選擇是一種常見的做法，因為研究者將大部分時間用在了其他算法設(shè)計上。

而該研究重新討論了 DQN 在低成本、小規(guī)模經(jīng)典控制和 MinAtar 環(huán)境中使用的損失函數(shù)和優(yōu)化器。研究者使用 Adam 優(yōu)化器進行了一些初始實驗，目前 Adam 優(yōu)化器是最流行的優(yōu)化器，并在實驗中結(jié)合使用了一個更簡單的損失函數(shù)，即均方誤差損失 (MSE）。由于在開發(fā)新算法時，優(yōu)化器和損失函數(shù)的選擇往往被忽略，而該研究發(fā)現(xiàn)在所有的經(jīng)典控制和 MinAtar 環(huán)境中，這二者的改變都能讓實驗結(jié)果有顯著的改進。

因此，研究者將兩個優(yōu)化器（RMSProp、Adam 優(yōu)化器）與兩個損失函數(shù)（Huber、MSE 損失）進行了不同的組合，并在整個 ALE 平臺（包含 60 款 Atari 2600 游戲）上進行了評估。結(jié)果發(fā)現(xiàn) Adam+MSE 組合優(yōu)于 RMSProp+Huber 組合。

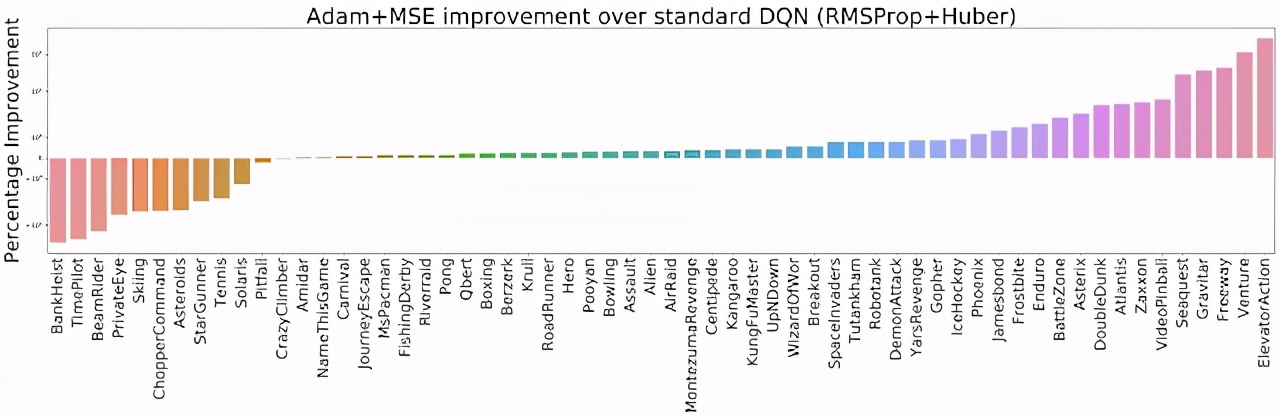
在默認(rèn) DQN 設(shè)置下（RMSProp + Huber），評估 Adam+MSE 組合帶來的改進（越高越好）。

此外，在比較各種「優(yōu)化器 - 損失函數(shù)」組合的過程中，研究者發(fā)現(xiàn)當(dāng)使用 RMSProp 時，Huber 損失往往比 MSE 表現(xiàn)得更好（實線和橙色虛線之間的間隙可以說明這一點）。

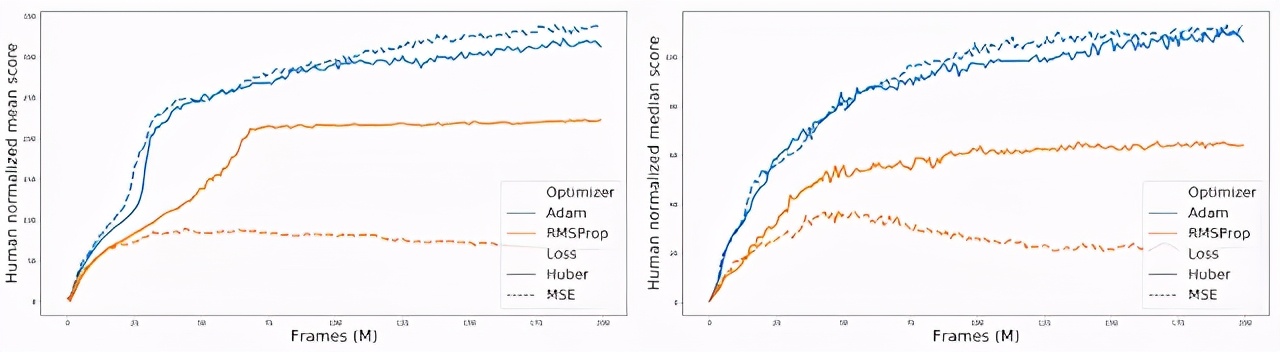
對 60 款 Atari 2600 游戲的標(biāo)準(zhǔn)化得分進行匯總，比較不同的「優(yōu)化器 - 損失函數(shù)」組合。

在有限的計算預(yù)算下，該研究研究者能夠在高層次上復(fù)現(xiàn)論文《Rainbow: Combining Improvements in Deep Reinforcement Learning》的研究，并且發(fā)現(xiàn)新的、有趣的現(xiàn)象。顯然，重新審視某事物比首次發(fā)現(xiàn)更容易。然而，研究者開展這項工作的目的是為了論證中小型環(huán)境實證研究的相關(guān)性和重要性。研究者相信，這些計算強度較低的環(huán)境能夠很好地對新算法的性能、行為和復(fù)雜性進行更關(guān)鍵和徹底的分析。該研究希望 AI 研究人員能夠把小規(guī)模環(huán)境作為一種有價值的工具，評審人員也要避免忽視那些專注于小規(guī)模環(huán)境的實驗工作。