[[426900]]

本文轉載自微信公眾號「高性能架構探索」，作者雨樂。轉載本文請聯系高性能架構探索公眾號。

今年，北京的雨尤其多，淅淅瀝瀝的。整個中秋節前兩天，都是在雨中度過，沒了往日中秋節的快樂氣氛，幸運的是，在中秋節當天，天氣晴朗，算是對整個假期畫上了個還算滿意的句號。

聽著淅淅瀝瀝的雨聲，想起前段時間在脈脈上看了一篇帖子，阿里P8去面試某條，掛在了一面算法上。而自己在3年前面試某公司，也栽在了同樣的一道算法上。正所謂吃一塹長一智，把該算法題重新整理了下，分享給大家，希望能夠有用。

接雨水

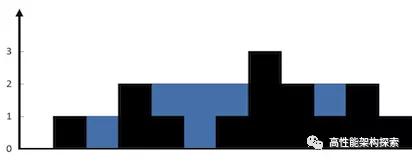
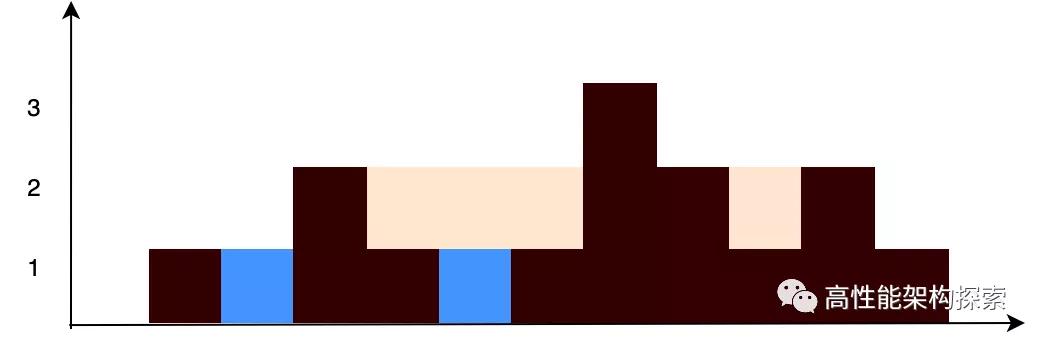
給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖，計算按此排列的柱子，下雨之后能接多少雨水。

接雨水

輸入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 輸出：6

解釋：上面是由數組[0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖，在這種情況下，可以接6個單位的雨水(藍色部分表示雨水)

看到題目的第一眼，感覺很簡單，但是卻不知道從何入手。下面我們將遵循循序漸進的方式，分析此題目的解法。

暴力解法

看到題目的一刻，出于思維定式，必定去查找"凹"型槽的最低部分，然后。。。，如此如此，越來越頭大，直至放棄。

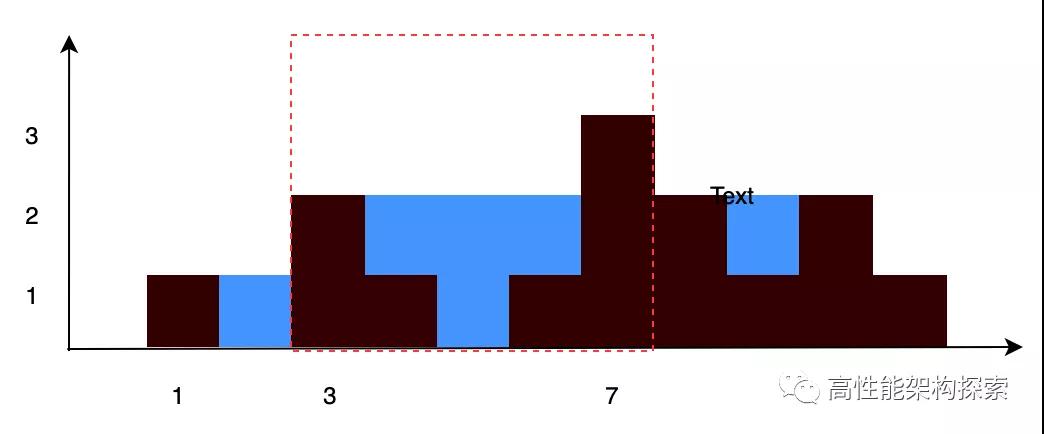
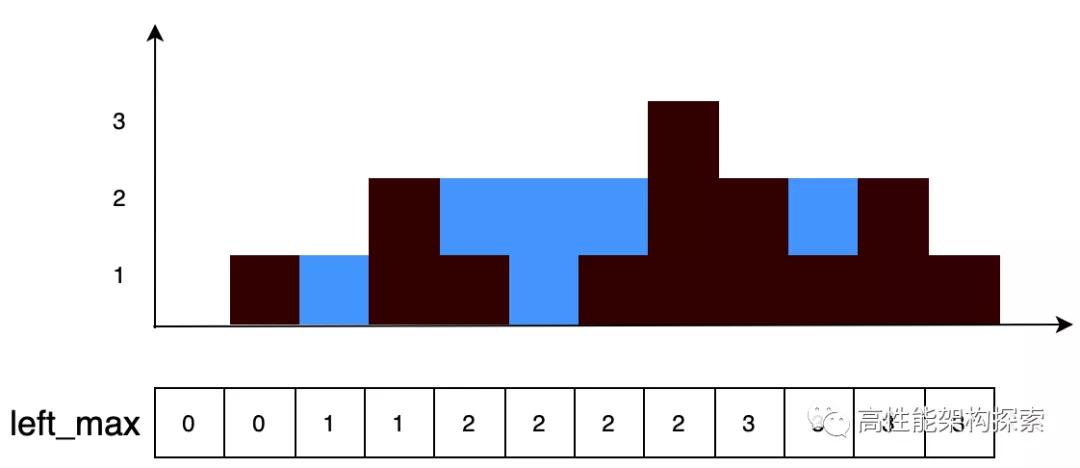
我們不妨換個思路，每根柱子上能放多少雨水。那么每根柱子上盛放雨水的高度怎么計算呢?就是其左右兩邊柱子最大高度的較小者與其高度之差，文字上理解起來比較費力，用圖的方式更加便于大家理解。

下面我們將計算柱子坐標(3)-(7)即紅框內的盛水量。

我們首先定義4個變量:

• res 盛水總量，其初始化為0
• height 當前柱子高度
• left_max 左邊最大高度(包括當前柱子本身
• right_max 右邊最大高度(包括其本身)

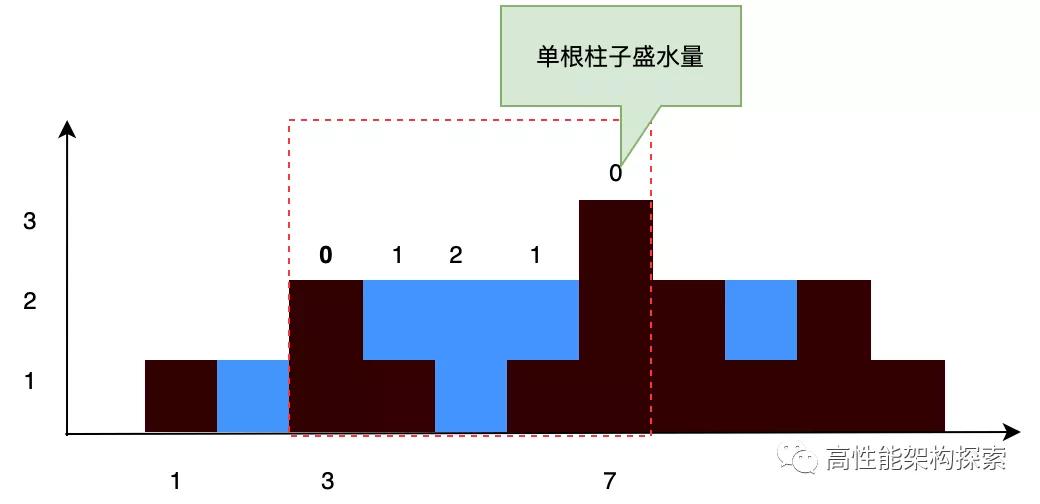
首先，計算柱子(3)處其盛水量。其左邊最大高度left_max為2，右邊最大高度right_max為3，那么橫坐標3處盛水量為min(left_max, right_max) - height 賦值之后為min(2, 3) - 2，答案為0，也就是說柱子(3)可盛水量為0。

接著我們計算柱子(4)處盛水量。按照上述計算規則，左邊最大高度為2，右邊最大高度為3，那么柱子(4)可盛水量為min(2, 3)- 1，答案為1。

然后計算柱子(5)處的盛水量，按照上述計算規則，左邊最大高度為2，右邊最大高度為3，那么柱子(5)可盛水量為min(2, 3)- 0，答案為2。

然后計算柱子(6)處的盛水量，按照上述計算規則，左邊最大高度為2，右邊最大高度為3，那么柱子(6)可盛水量為min(2, 3)- 1，答案為1。

最后計算柱子(7)處的盛水量，左邊最大高度為3，右邊最大高度為3，那么柱子(7)可盛水量為min(3, 3) - 3即0.

因此，柱子(3)到柱子(7)之間所盛水量res = 0 + 1 + 2 + 1 + 0 = 4.

代碼實現一：

int trap(vector<int>& height) { 
  int res = 0; 
   
  for (int cur = 0; cur < height.size(); ++cur) { 
    int left_max = 0; 
    int right_max = 0; 
     
    // 計算左邊最大高度 
    for (int left = 0; left <= cur; ++left) { 
       left_max = std::max(left_max, height[left]); 
    } 
     
    // 計算右邊最大高度 
    for (int right = cur; right < height.size(); ++right) { 
      right_max = std::max(right_max, height[right]); 
    } 
     
    // 計算總盛水量 
    res += std::min(left_max, right_max) - height[cur]; 
  } 
   
  return res; 
} 

上述規則有個trick，就是計算兩邊最高的時候，都將柱子本身的高度計算在內，這樣做是為了在計算盛水量的時候，方便計算。

假設計算柱子(3)，如果在計算兩邊最大高度的時候不包括柱子(3)本身的高度，那么柱子(3)左邊最大高度為1，右邊最大高度為3，在計算盛水量的時候，就需要判min(lext_max, right_max)與柱子(3)本身的大小，否則會出現負值，代碼實現如下。

代碼實現二

int trap(vector<int>& height) { 
  int res = 0; 
   
  for (int cur = 0; cur < height.size(); ++cur) { 
    int left_max = 0; 
    int right_max = 0; 
     
    // 計算左邊最大高度 
    // 注意，與實現一相比，left到cur的前一個截止 
    for (int left = 0; left < cur; ++left) { 
       left_max = std::max(left_max, height[left]); 
    } 
     
    // 計算右邊最大高度 
    // 注意，與實現一相比，right從下一個開始 
    for (int right = cur + 1; right < height.size(); ++right) { 
      right_max = std::max(right_max, height[right]); 
    } 
     
    // 計算總盛水量 
    int mx = std::min(left_max, right_max); 
    if (mx > height[cur]) { // 需要進行判斷 
      res += mx - height[cur]; 
    } 
  } 
   
  return res; 
} 

暴力解法，理解起來簡單，時間復雜度為O(n2),提交之后，毫無疑問會TLE，下面我們從其他方面對暴力法進行優化。

為了便于理解，后面的實現將使用實現二的思想。

動態規劃

看了暴力法的實現，我們基本思路已經有了，其時間復雜度為O(n2)，時間主要消耗在查找兩邊最大柱子高度上。那么有沒有什么辦法，能夠 常數次 遍歷就能獲取到所有柱子的兩邊高度呢?

我們仍然以

height = [0,1,0,2,1,0,1,3,2,1,2,1] 

為例，計算雙邊最大值。

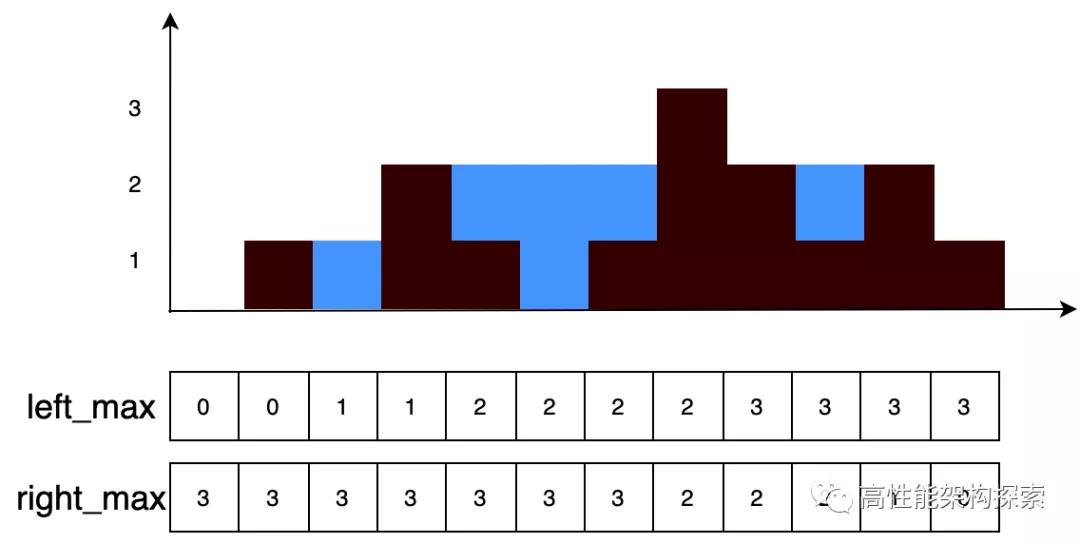
左側最大值

定義數組left_max，其中left_max[i]代碼第i個柱子左邊最大高度。

下面我們來計算柱子左側的最大高度：

• 柱子(0)，左側最大高度為0(其左側沒有柱子)
• 柱子(1)，左側最大高度為0(左側只有柱子0)
• 柱子(2)，左側最大高度為1([0 1]數組的最大值)
• 柱子(3)，左側最大高度為1([0 1 0]數組最大值)
• 柱子(4)，左側最大高度為2([0 1 0 2]數組最大值)
• 柱子(5)，左側最大高度為2([0 1 0 2 1]數組最大值)
• 柱子(6)，左側最大高度為2([0 1 0 2 1 0]數組最大值)
• 柱子(7)，左側最大高度為2([0 1 0 2 1 0 1]數組最大值)
• 柱子(8)，左側最大高度為3([0 1 0 2 1 0 1 3]數組最大值)
• 柱子(9)，左側最大高度為3([0 1 0 2 1 0 1 3 2]數組最大值)
• 柱子(10)，左側最大高度為3([0 1 0 2 1 0 1 3 2 1]數組最大值)
• 柱子(11)，左側最大高度為3([0 1 0 2 1 0 1 3 2 1 2]數組最大值)

左側最大值

從上述規則，我們進行分析，發現有一定的規律可循，即當前柱子左側最大高度 為 max(上一個柱子左側最大高度, 上一個柱子高度)。

代碼表示如下:

std::vector<int> left_max(height.size(), 0); 
for (int i = 1; i < height.size(); ++i) { 
  left_max[i] = std::max(left_max[i - 1], height[i]); 
} 

對上述代碼進行稍許變化后如下：

std::vector<int> left_max(height.size(), 0); 
int mx = 0; 
for (int i = 0; i < height.size(); ++i) { 
  left_max[i] = mx; 
  mx = std::max(mx, height[i]); 
} 

右側最大值

定義數組right_max，其中left_max[i]代碼第i個柱子右邊最大高度。

因為要計算右側最大值，所以必須從最后一個開始向前計算(如果從第一個開始計算的，那么跟暴力法沒區別了)。height = [0,1,0,2,1,0,1,3,2,1,2,1]

• 柱子(11)，右側最大高度為0(其右側沒有柱子)
• 柱子(10)，右側最大高度為1([1]的最大值)
• 柱子(9)，右側最大高度為2([2 1]的最大值)
• 柱子(8)，右側最大高度為2([1 2 1]的最大值)
• 柱子(7)，右側最大高度為2([2 1 2 1]的最大值)
• 柱子(6)，右側最大高度為3([3 2 1 2 1]的最大值)
• 柱子(5)，右側最大高度為3([1 3 2 1 2 1]的最大值)
• 柱子(4)，右側最大高度為3([0 1 3 2 1 2 1]的最大值)
• 柱子(3)，右側最大高度為3([1 0 1 3 2 1 2 1]的最大值)
• 柱子(2)，右側最大高度為3([2 1 0 1 3 2 1 2 1]的最大值)
• 柱子(1)，右側最大高度為3([0 2 1 0 1 3 2 1 2 1]的最大值)
• 柱子(0)，右側最大高度為3([1 0 2 1 0 1 3 2 1 2 1]的最大值)

右側最大值

既然計算出來了雙邊最大值，那么我們來實現下代碼：

int trap(vector<int>& height) { 
  int res = 0; 
  std::vector<int> left_max(height.size());  
  std::vector<int> right_max(height.size());  
  int mx = 0; 
   
  // 循環一、計算左側最大值 
  for (int i = 0; i < height.size(); ++i) { 
    left_max[i] = mx; 
    mx = std::max(mx, height[i]); 
  } 
   
  mx = 0; 
  // 循環二、計算右側最大值 
  for (int i = height.size() - 1; i >= 0; --i) { 
    right_max[i] = mx; 
    mx = std::max(mx, height[i]); 
  } 
   
  // 循環三、計算所盛雨水量 
  for (int i = 0; i < height.size(); ++i) { 
    int mn = std::min(left_max[i], right_max[i]); 
    if (mn > height[i]) { 
      res += mn - height[i]; 
    } 
  } 
   
  return res; 
} 

上述代碼較暴力方法優化后，時間復雜度優化為O(n), 提交后AE。

動態規劃

上述代碼中有3個循環，空間復雜度為O(2n)，又作為c++ coder這是不能忍的，能不能再進行優化呢?我們看到循環三單純為計算盛雨量，能否將循環二和循環3合并，并且優化空間復雜度呢?必須可以，為了閱讀起來方便，我們實現代碼如下：

int trap(vector<int>& height) { 
  int res = 0; 
  std::vector<int> v(height.size());  
  int mx = 0; 
   
  // 循環一、計算左側最大值 
  for (int i = 0; i < height.size(); ++i) { 
    v[i] = mx; 
    mx = std::max(mx, height[i]); 
  } 
   
  mx = 0; 
  // 循環二、計算右側最大值 并 計算盛水量 
  for (int i = height.size() - 1; i >= 0; --i) { 
    int mn = std::min(mx, v[i]); 
    mx = std::max(mx, height[i]); 
    if (mn > height[i]) { 
      res += mn - height[i]; 
    } 
  } 
   
  return res; 
} 

優化后的動態規劃

雙指針

動態規劃方法，時間復雜度和空間復雜度都是O(n)，下面我們介紹一種只有一次循環且空間復雜度為O(1)的算法，這就是雙指針算法。

接雨水算法的核心思想，就是計算當前柱子的盛水量，也就是左右兩邊的最大值的較小者與當前柱子之差。我們先求出數組雙端柱子的較小值，然后兩邊柱子跟這個較小值相比較，如果較小值為左邊的柱子，則左邊柱子向右移動，直至比當前較小值大。反之，如果較小值為右側柱子，則右側柱子向左移動，直至比當前值大。

left 和 right 兩個指針分別指向數組的首尾位置，從兩邊向中間掃描，在當前兩指針確定的范圍內，先比較兩頭找出較小值，如果較小值是 left 指向的值，則從左向右掃描，如果較小值是 right 指向的值，則從右向左掃描，若遇到的值比當較小值小，則將差值存入結果，如遇到的值大，則重新確定新的窗口范圍，以此類推直至 left 和 right 指針重合

int trap(vector<int>& height) { 
  int res = 0; 
  int left = 0; 
  int right = height.size() - 1; 
  while (left < right) { 
    int mn = min(height[left], height[right]); 
    if (mn == height[left]) { 
      ++left; 
      while (left < right && height[left] < mn) { 
        res += mn - height[left++]; 
      } 
    } else { 
      --right; 
      while (left < right && height[right] < mn) { 
        res += mn - height[right--]; 
      } 
    } 
  } 
  return res; 
} 

單調棧

此種方法較前面的兩種(暴力法和雙指針法)，如果說前面兩種方法都是求每根柱子上盛水量之和的話(即 按列計算)，那么單調棧方法則是 按行計算 每一層的盛水量，如下圖所示：

逐層計算

每一行水左右肯定都會被柱子卡住。那么從左向右遍歷柱子，如果高度在下降，那么顯然不會蓄水。如果高度上升了，那就說明中間是個低點，這之間可以蓄水。而這個下降的高度用單調棧來維護就行了，棧里我們只放下標。

遍歷高度，如果此時棧為空，或者當前高度小于等于棧頂高度，則把當前高度的坐標壓入棧，注意這里不直接把高度壓入棧，而是把坐標壓入棧，這樣方便在后來算水平距離。當遇到比棧頂高度大的時候，就說明有可能會有坑存在，可以裝雨水。此時棧里至少有一個高度，如果只有一個的話，那么不能形成坑，直接跳過，如果多余一個的話，那么此時把棧頂元素取出來當作坑，新的棧頂元素就是左邊界，當前高度是右邊界，只要取二者較小的，減去坑的高度，長度就是右邊界坐標減去左邊界坐標再減1，二者相乘就是盛水量。

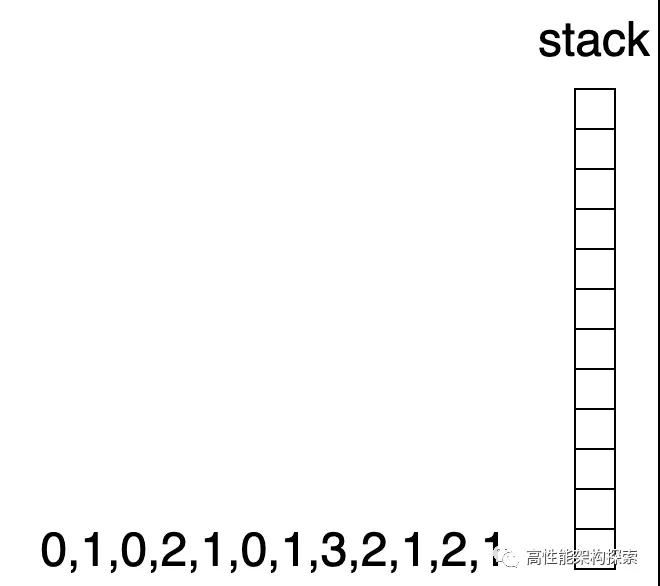
我們仍然以數組height = [0,1,0,2,1,0,1,3,2,1,2,1]為例來說明單調棧的用法。

假設res初始值為0，用其來計算height數組所表示的柱子高度最大盛水量。

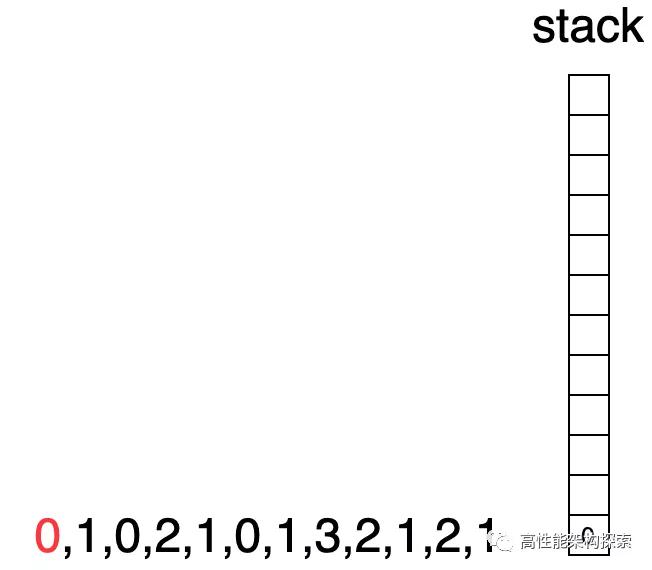
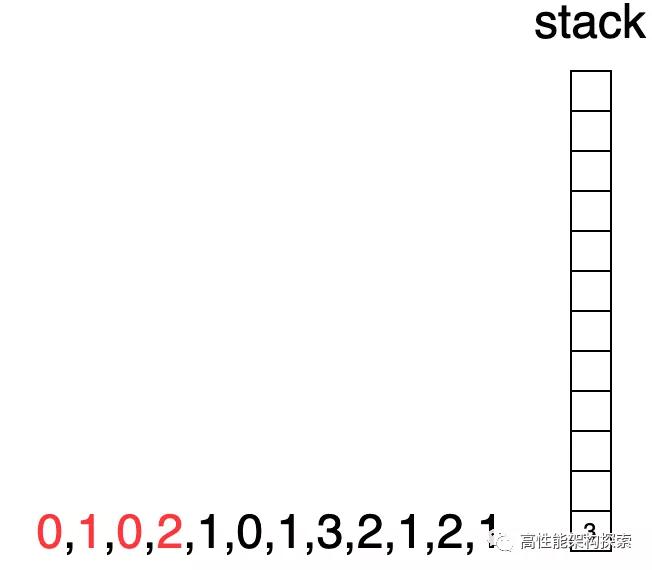
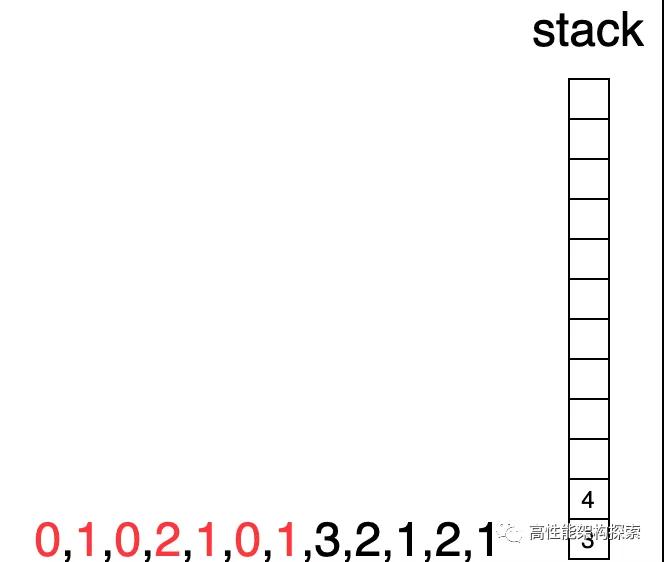
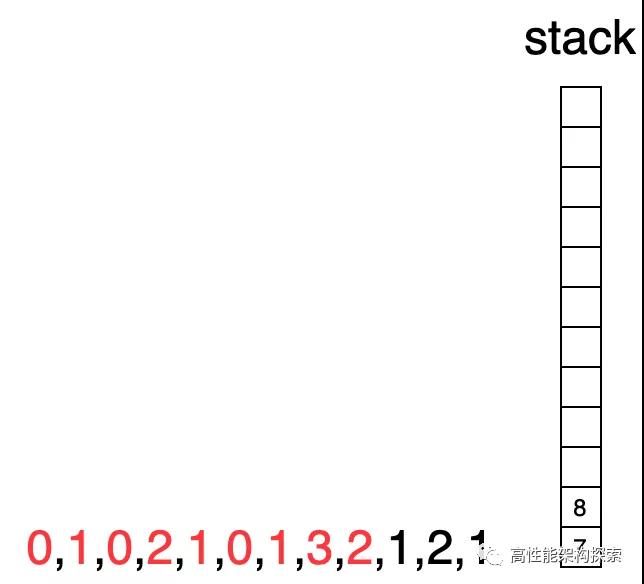
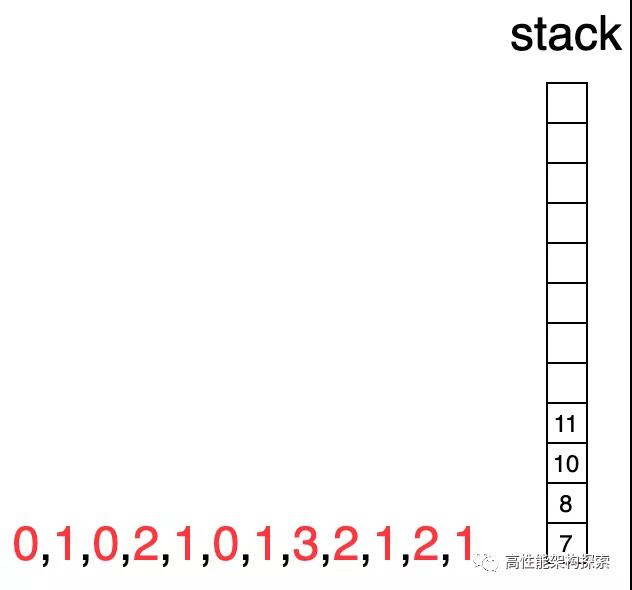
• 初始化時候，棧為空。

棧為空

• 因為棧為空，所以下標0入棧，如下圖所示：



• 由于下標1所指向的數組height[1] = 1大于棧頂下標所指向的數，所以下標0出棧，下標1入棧。



• 由于下標2指向的值小于棧頂值，則下標2入棧。

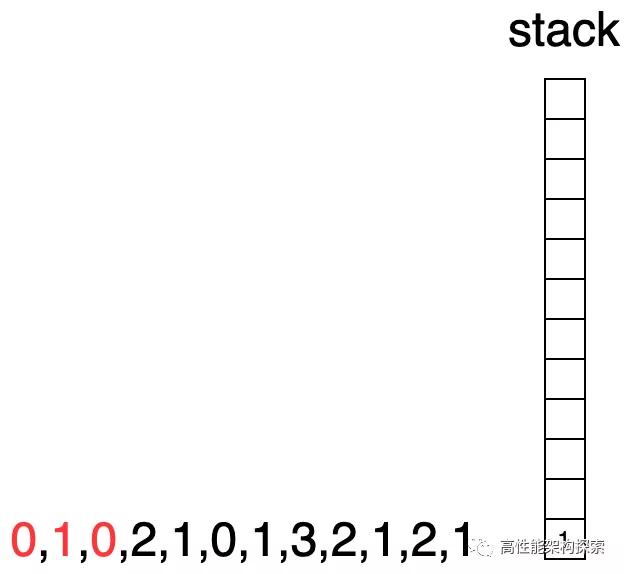
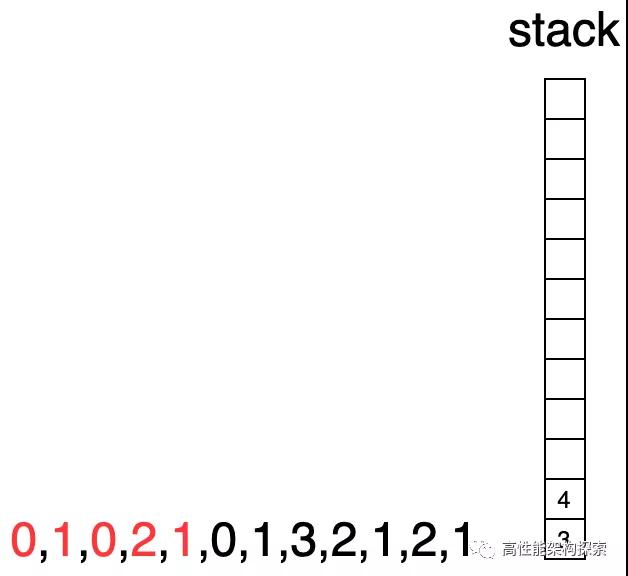
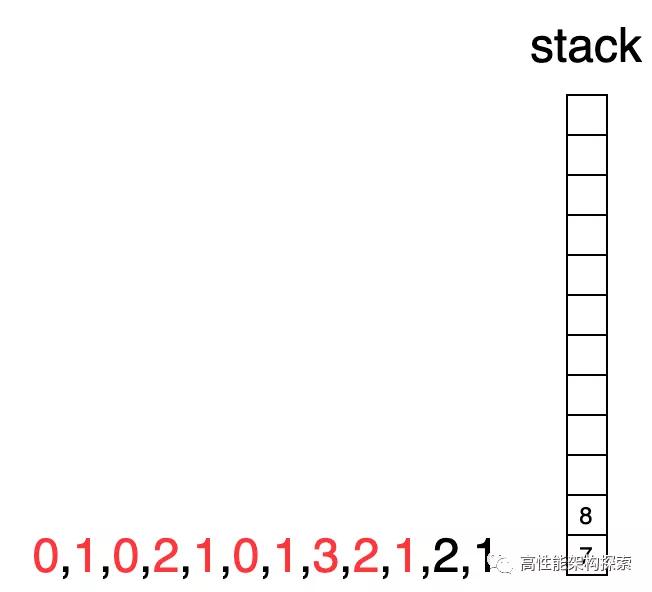
此時下標指向3，由于下標3指向的值大于棧頂下標指向的值，則出棧，計算增量盛水量((min(2, 1) - 0) * (3 - 1 - 1) = 1)，即增量為1，此時res = 1。

• 由于下標1所指向的高度小于下標3指向高度，則下標1出棧，此時棧為空，則下標3進棧。



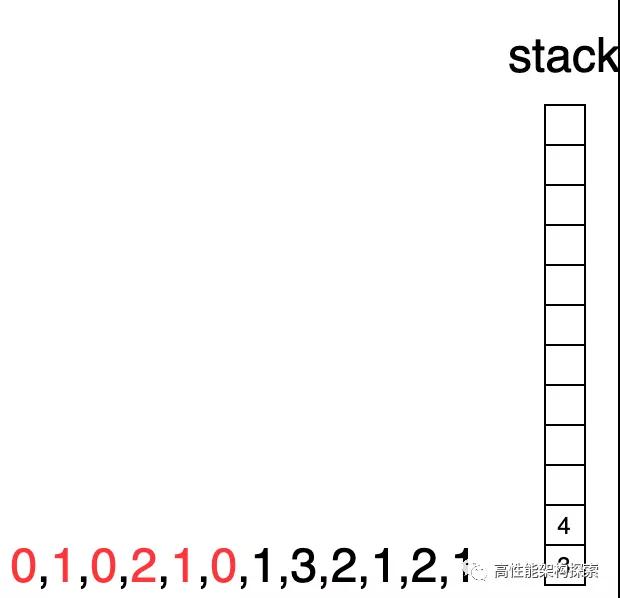
• 下標4指向的值小于棧頂下標指向的值(1 < 2),下標4入棧



• 下標5指向的值小于棧頂下標指向的值(0 < 1),下標5入棧



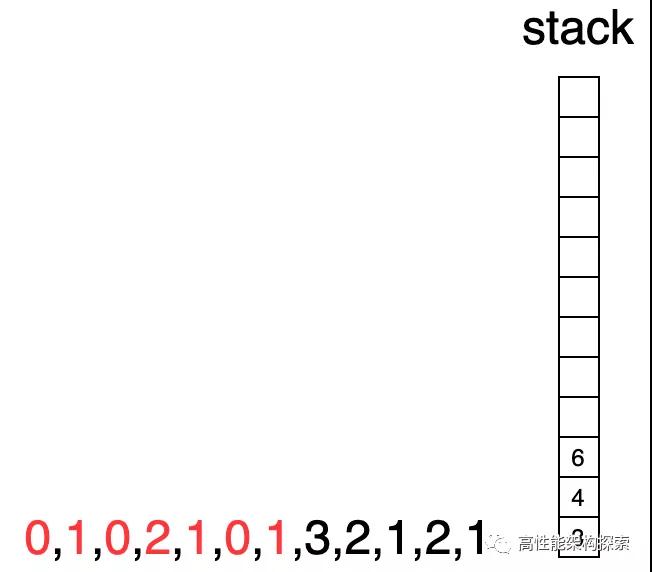
• 此時下標6指向的值為1，大于棧頂下標所指向的值(1 > 0)，則執行出棧，同時計算盛水增量((min(1, 1) - 0) * (6 - 4 - 1)),增量為1，此時res = 1 + 1 = 2。



• 下標6所指向的值等于棧頂指向的值(1 = 1),下標6入棧

• 此時下標指向7，其值大于棧頂值(3 > 1)，則棧頂出棧，計算增量為((min(3, 1) - 1) * (7 - 4 - 1)),增量為0，此時res = 1 + 1 + 0 = 2

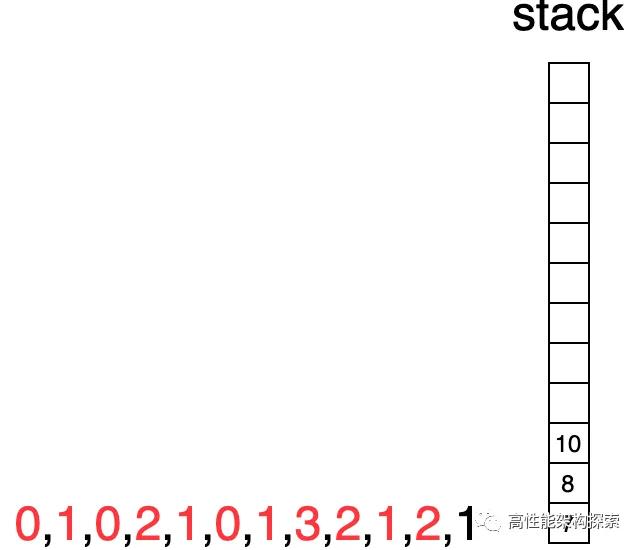
• 此時，下標仍為7，棧頂值為4，由于當前下標指向值大于棧頂指向值，則出棧，計算盛水增量((min(3, 2) - 1) * (7 - 3 - 1)),增量為3，此時res = 1 + 1 + 0 + 3 = 5

計算增量盛水量

• 此時棧內只有下標3，且其所指向值小于當前下標指向值(2 < 3)，則出棧

下標3出棧

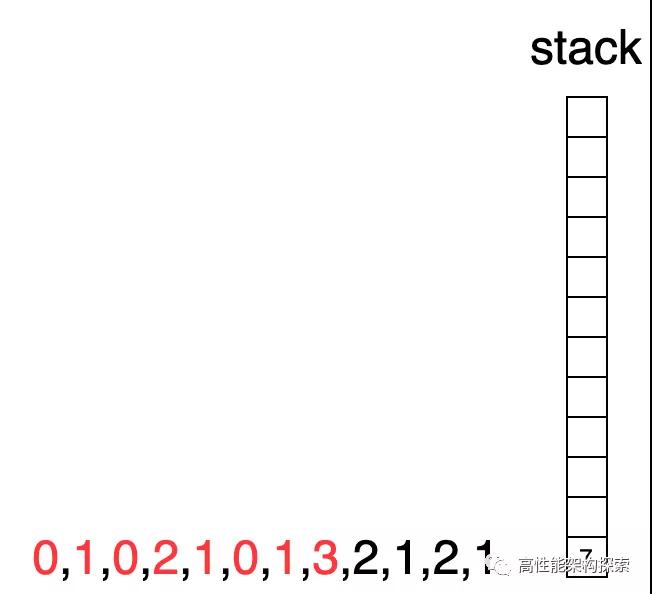
此時棧為空，則下標7入棧

• 下標8指向值小于棧頂指向值(2 < 3),下標8入棧



• 下標9指向值小于棧頂指向值(1 < 2),下標9入棧



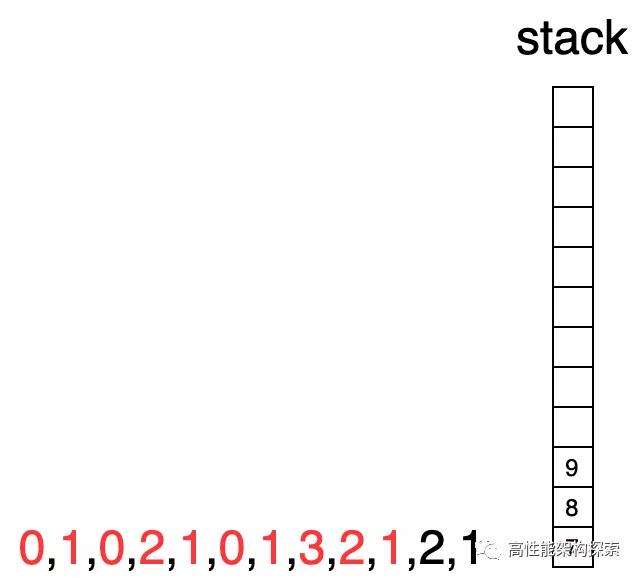
• 此時下標為10，其對應值大于棧頂指向值(2 > 1)，則棧頂出棧，并計算增量((min(2, 2) - 1) * (10 - 8 - 1)),增量為1，此時res = 1 + 1 + 0 + 3 + 1 = 6



• 下標10指向值小于棧頂值，入棧

下標11指向值小于棧頂值，入棧

此時，數組循環結束，盡管棧內還有數，坐標為7 8 10 11，指向的值為3 2 2 1，但其已經不能構成一個凹槽進行盛水，所以算法執行結束。

代碼實現如下：

int trap(vector<int>& height) { 
  stack<int> st; 
  int i = 0, res = 0, n = height.size(); 
  while (i < n) { 
    if (st.empty() || height[i] <= height[st.top()]) { 
    st.push(i++); 
} else { 
    int t = st.top(); st.pop(); 
    if (st.empty()) continue; 
    res += (min(height[i], height[st.top()]) - height[t]) * (i - st.top() - 1); 
    } 
  } 
  return res; 
} 

寫在最后

架構或者底層原理分析方面，需要調研大量的資料，研究分析源碼，很耗費精力。所以后面的文章中，可能會有算法(leetcode經典算法)、面試(針對面試中遇到的一些經典問題)以及架構和底層穿插發表。