幾個有趣的算法,你知道嗎?
本文轉載自微信公眾號「微醫大前端技術」,作者孫領芝 。轉載本文請聯系微醫大前端技術公眾號。
根據身份證號碼計算出性別、年齡
一、身份證號碼國家標準
1、范圍
《公民身份號碼》(GB11643-1999)該標準規定了公民身份號碼的編碼對象、號碼的結構和表現形式,使每個編碼對象獲得一個唯一的、不變的法定號碼。
2、號碼的結構
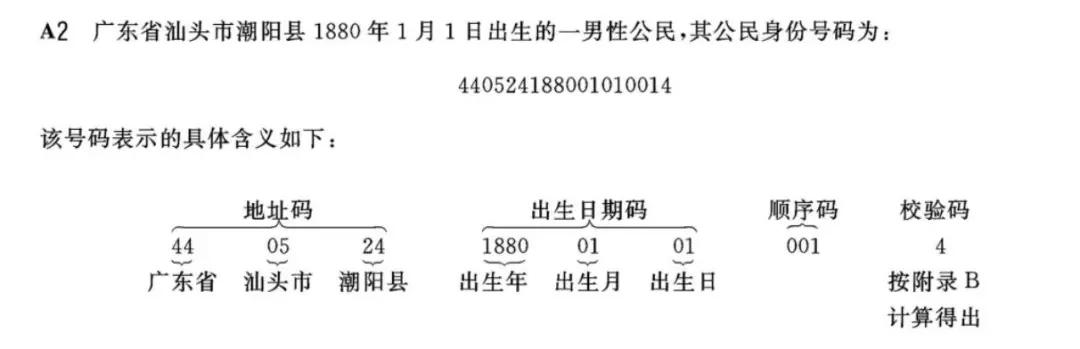
公民身份號碼是特征組合碼,由十七位數字本體碼和一位校驗碼組成。排列順序從左至右依次為:六位數字地址碼,八位數字出生日期碼,三位數字順序碼和一位數字校驗碼。
2.1、地址碼
表示編碼對象常住戶口所在縣(市、旗、區)的行政區劃代碼
2.2、出生日期碼
表示編碼對象出生的年、月、日
2.3、順序碼
表示在同一地址碼所標識的區域范圍內,對同年、同月、同日出生的人編定的順序號,順序碼的奇數分配給男性,偶數分配給女性。
2.4、校驗碼
根據前面十七位數字碼,按照 ISO 7064:1983.MOD 11-2 中的校驗碼計算方法計算確定
(1)十七位數字本體碼加權求和公式:S = Sum(Ai * Wi)
| 身份證號 | 1 | 1 | 0 | 1 | 0 | 5 | 1 | 9 | 4 | 9 | 1 | 2 | 3 | 1 | 0 | 0 | 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 加權因子 | 7 | 9 | 10 | 5 | 8 | 4 | 2 | 1 | 6 | 3 | 7 | 9 | 10 | 5 | 8 | 4 | 2 |
| Ai * Wi | 7 | 9 | 0 | 5 | 0 | 20 |
S = 7 + 9 + 0 + 5 + 0 + 20 + 2 + 9 + 24 + 27 + 7 + 18 + 30 + 5 + 0 + 0 + 4 = 167
(2)計算模:Y = mod(S, 11) Y = 167 % 11 => 2
(3)通過模得到對應的校驗碼
| 模 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 校驗碼 | 1 | 0 | X | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
模為 2 時,校驗碼為 X。
二、代碼實現
1、身份證號正確性校驗
- const WEIGHT = [7,9,10,5,8,4,2,1,6,3,7,9,10,5,8,4,2]
- const MO = [1,0,'X',9,8,7,6,5,4,3,2]
- function isRightId(id){
- const arr = id.split('')
- const checkNumber = arr.pop() // 去除校驗碼,將 pop 的返回值賦值給 checkNumber
- let sum = 0
- arr.forEach((ele, index) => {
- sum += ele * WEIGHT[index]
- })
- const m = sum % 11
- const result = MO[m]
- return result+'' === checkNumber
- }
- console.log(isRightId('11010519491231002X')) // true
- console.log(isRightId('110105194912310029')) // false
2、由身份證號計算年齡
- function getAge(id){
- // 1、先判斷身份證號的正確性
- // 2、判斷是否在世
- const year = id.substr(6,4)
- const month = id.substr(10,2)
- const day = id.substr(12,2)
- const timeBrth = new Date(`${year}/${month}/${day}`).getTime()
- const timeNow = new Date().getTime()
- const longTime = timeNow - timeBrth
- const days = longTime / (1*24*60*60*1000)
- let result = ''
- if(days<31){
- result = parseInt(days) + '天'
- }else if(days<365){
- result = `${parseInt(days/30)}月${parseInt(days%30)}天`
- }else{
- result = `${parseInt(days/365)}歲${parseInt(days%365/30)}月${parseInt(days%365%30)}天`
- }
- return result
- }
- console.log(getAge('11010519491231002X')) // 71 歲 8 月 16 天
- console.log(getAge('11010520210820002X')) // 6 天
- console.log(getAge('11010520210720002X')) // 1 月 7 天
3、由身份證號判斷性別
- function getSex(id){
- // 1、先判斷身份證號的正確性
- const sex = id.substr(16,1)
- return sex%2? '男': '女'
- }
- console.log(getSex('11010519491231002X')) // 女
- console.log(getSex('11010520210820001X')) // 男
三、其他
1、變性手術后,身份證號碼是否更改?
跨性別人士身份證性別變更后,依戶口所在派出所公示為準,進行身份證號碼變更。
2、計算年齡前應先確認是否在世。
四、參考資料
《公民身份號碼》(GB11643-1999)
動態規劃
1、定義
動態規劃(Dynamic Programming,DP)是運籌學的一個分支,是求解決策過程最優化的過程。
可以簡單的理解為是對傳統遞歸的一種優化。在 DP 的實踐中很重要的就是遞推關系和邊界條件。
2、簡單:爬樓梯
題目
假設你正在爬樓梯。需要 n 階你才能到達樓頂。
每次你可以爬 1 或 2 個臺階。你有多少種不同的方法可以爬到樓頂呢?
注意 給定 n 是一個正整數。
- 輸入:2
- 輸出:2
- 解釋: 有兩種方法可以爬到樓頂。
- 1. 1 階 + 1 階
- 2. 2 階
示例 2:
- 輸入:3
- 輸出:3
- 解釋: 有三種方法可以爬到樓頂。
- 1. 1 階 + 1 階 + 1 階
- 2. 1 階 + 2 階
- 3. 2 階 + 1 階
代碼:
- // 把數據緩存在一個數組中
- var climbStairs = function(n) {
- let dp = []
- dp[0]=1;
- dp[1]=1;
- for(let i=2;i<=n;i++){
- dp[i]=dp[i-1]+dp[i-2];
- }
- return dp[n];
- };
- // 使用遞歸
- var climbStairs = function(n) {
- if(n===1) return 1
- if(n===2) return 2
- return climbStairs(n-1) + climbStairs(n-2)
- };
思路:
f(x)=f(_x_?1)+f(x_?2) 爬到第 x _級臺階的方案數是爬到第 x - 1 級臺階的方案數和爬到第 x - 2 級臺階的方案數的和。
LeetCode 運行結果:
3、中等:最長回文子串
題目
給你一個字符串 s,找到 s 中最長的回文子串。
示例 1:
- 輸入:s = "babad"
- 輸出:"bab"
- 解釋:"aba" 同樣是符合題意的答案。
示例 2:
- 輸入:s = "cbbd"
- 輸出:"bb"
思路:
當 s[i+1 : j-1] 是回文串,并且 s 的第 i 和 j 個字母相同時,s[i:j] 才會是回文串。
即:P(i,j)=P(i+1,j?1) 且 (Si == Sj)。
邊界條件:子串的長度為 1 或 2。對于長度為 1 的子串,它顯然是個回文串;對于長度為 2 的子串,只要它的兩個字母相同,它就是一個回文串。
- P(i, i) = true
- P(i, i+1) = (Si == Si+1)
代碼:
- function longestPalindrome (s) {
- // 先判斷字符串長度,如果為 1 則直接返回
- let len = s.length
- if (len < 2) return s
- // 初始化變量
- let maxLen = 1
- let begin = 0
- // dp[i][j] 表示 s[i..j] 是否是回文串
- let dp = []
- // 初始化:所有長度為 1 的子串都是回文串
- for (let i = 0; i < len; i++) {
- dp[i] = []
- dp[i][i] = true
- }
- // 將字符串切割為數組
- let charArray = s.split('')
- // 遞推開始
- for (let L = 2; L <= len; L++) { // 枚舉子串長度
- // 枚舉左邊界,左邊界的上限設置可以寬松一些
- for (let i = 0; i < len; i++) {
- // 由 L 和 i 可以確定右邊界,即 j - i + 1 = L 得
- let j = L + i - 1;
- // 如果右邊界越界,退出當前循環
- if (j >= len) {
- break;
- }
- // 判斷是否為回文
- if (charArray[i] !== charArray[j]) {
- dp[i][j] = false
- } else {
- // 對于一個子串而言,如果它是回文串,并且長度大于 2,那么將它首尾的兩個字母去除之后,它仍然是個回文串。
- let flag = j - i < 3
- dp[i][j] = flag ? true : dp[i + 1][j - 1]
- }
- // 當 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,記錄回文長度和起始位置
- if (dp[i][j] && j - i + 1 > maxLen) {
- maxLen = j - i + 1;
- begin = i;
- }
- }
- }
- return s.substring(begin, begin + maxLen);
- }
- console.log(longestPalindrome('babad'), 'babad') // bab babad
- console.log(longestPalindrome('cbbd'), 'cbbd') // bb cbbd
LeetCode 運行結果:
4、困難:接雨水
題目:
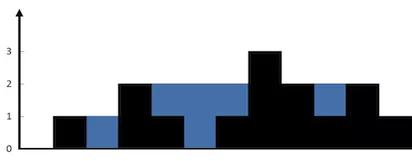
給定 n 個非負整數表示每個寬度為 1 的柱子的高度圖,計算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
- 輸入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 輸出:6
- 解釋:上面是由數組 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度圖,在這種情況下,可以接 6 個單位的雨水(藍色部分表示雨水)。
示例 2:
- 輸入:height = [4,2,0,3,2,5]
- 輸出:9
代碼:
- function trap(height) {
- // 不滿足條件,直接返回
- let len=height.length;
- if(len<=2) return 0;
- let maxLeft = []; // 第 i 根柱子左邊最高柱子的高度
- let maxRight = []; // 第 i 根柱子右邊最高柱子的高度
- maxLeft[0] = height[0];
- for(let i=1; i<len; i++){
- maxLeft[i] = Math.max(height[i], maxLeft[i-1]) // 動態轉移
- }
- maxRight[len-1] = height[len-1];
- for(let j=len-2; j>=0; j--){
- maxRight[j] = Math.max(height[j], maxRight[j+1]) // 動態轉移
- }
- let sum=0;
- for(let i=0;i<len;i++) sum+=Math.min(maxLeft[i],maxRight[i])-height[i];
- return sum;
- }
思路:
每一列柱子接的雨水是該柱子兩側最高柱子的最小值減去該柱子高度。
LeetCode 運行結果:
附件:雙指針法
代碼:
- function trap(height) {
- let ans=0;
- for(let i=1; i<height.length-1; i++){
- let l_hight = height[i];
- let r_hight = height[i];
- // 找到 i 列右側最高柱子高度
- for(let r=i; r<height.length; r++){
- if(height[r]>r_hight) r_hight=height[r];
- }
- // 找到 i 列柱子左側最高柱子高度
- for(let l=i; l>=0; l--){
- if(height[l]>l_hight) l_hight=height[l];
- }
- ans+=Math.min(l_hight,r_hight)-height[i];
- }
- return ans;
- }
LeetCode 運行結果:
5、參考資料
來源:力扣(LeetCode)
https://leetcode-cn.com/problems/climbing-stairs/
https://leetcode-cn.com/problems/longest-palindromic-substring/
https://leetcode-cn.com/problems/trapping-rain-water/
貪心算法
1、定義
在對問題求解時,總是做出在當前看來是最好的選擇。
2、分餅干
假設你是一位很棒的家長,想要給你的孩子們一些小餅干。但是,每個孩子最多只能給一塊餅干。對每個孩子 i,都有一個胃口值 g[i],這是能讓孩子們滿足胃口的餅干的最小尺寸;并且每塊餅干 j,都有一個尺寸 s[j] 。如果 s[j] >= g[i],我們可以將這個餅干 j 分配給孩子 i ,這個孩子會得到滿足。你的目標是盡可能滿足越多數量的孩子,并輸出這個最大數值。
示例 1: 輸入: g = [1,2,3], s = [1,1] 輸出: 1
示例 2: 輸入: g = [1,2], s = [1,2,3] 輸出: 2
- function findContentChildren1(children, cookies){
- children = children.sort((a, b) => a - b)
- cookies = cookies.sort((a, b) => a - b)
- let childrenLength = children.length
- let cookiesLength = cookies.length
- let count = 0
- for(let i = 0, j = 0; i < childrenLength && j < cookiesLength; i++, j++){
- while(j < cookiesLength && children[i] > cookies[j]){
- j++
- }
- if(j < cookiesLength){
- count++
- }
- }
- return count
- }
- console.log(findContentChildren1([1,2,3], [1,1])) // 1
- console.log(findContentChildren1([1,2], [1,2,3])) // 2
- console.log(findContentChildren1([1,2,3], [1,1,3,4])) // 3
核心思想:
- 將孩子的胃口、餅干的大小都按照從小到大排序。
- for 循環遍歷,比較孩子的胃口 children[i]和餅干的大小 cookies[j]之間的關系,當當前餅干不能滿足孩子的胃口時,選擇下一個餅干進行比較。
- 如果滿足孩子的胃口,且 j 在范圍內,則 count 加 1。
代碼解讀:
- 定義函數 findContentChildren,接受 2 個參數,分別為 children:孩子的胃口,cookies 餅干的大小。
- 將 children 和 cookies 按照從小到大排序。
- 定義能夠滿足孩子胃口的個數 count,并最終將 count 返回。
- 循環遍歷,當 children[i] > cookies[j] 即當前餅干不能滿足孩子時,j++選擇下一塊餅干進行比較。
- 如果 children[i] <= cookies[j] 即當前餅干能滿足孩子,且 j 在范圍內,則 count 加 1。
- 進入下一次循環(即嘗試滿足下一個孩子)。
3、買股票
給定一個整數數組 prices,其中第 i 個元素代表了第 i 天的股票價格 ;整數 fee 代表了交易股票的手續費用。你可以無限次地完成交易,但是你每筆交易都需要付手續費。如果你已經購買了一個股票,在賣出它之前你就不能再繼續購買股票了。返回獲得利潤的最大值。注意:這里的一筆交易指買入持有并賣出股票的整個過程,每筆交易你只需要為支付一次手續費。
示例 1:輸入:prices = [1, 3, 2, 8, 4, 9], fee = 2, 輸出:8
解釋:
能夠達到的最大利潤:
在此處買入 prices[0] = 1 在此處賣出 prices[3] = 8 在此處買入 prices[4] = 4 在此處賣出 prices[5] = 9 總利潤: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2:輸入:prices = [1,3,7,5,10,3], fee = 3 輸出:6
- function maxProfit(list, fee){
- const length = list.length
- let buy = list[0] + fee // 假定:買入時機為第 1 天
- let profit = 0
- for(let i = 1; i < length; i++){
- if(list[i]+fee < buy){ // 如果股票價格降低,則調整買入時機
- buy = list[i]+fee
- }else if(list[i] > buy){ // 如果有利潤,則賣出
- profit += list[i] - buy // 計算利潤
- buy = list[i] // 調整買入時機
- }
- }
- return profit
- }
- console.log(maxProfit([1, 3, 2, 8, 4, 9], 2)) // 8
- console.log(maxProfit([1,3,7,5,10,3], 3)) // 6
代碼解讀:
- 定義函數 maxProfit,接受 2 個參數,list 為股票價格趨勢,fee 為手續費
- 定義 profit,并在最后將 profit 返回
- 假定:買入時機為第 1 天(即:list[0])
- 如果股票價格降低,則調整買入時機為后一天
- 如果有利潤,則賣出,并計算利潤,再次調整買入時機(即循環步驟 3、4、5)
核心思想:
- 假定:買入時機為第 1 天
- 如果股票價格降低,則調整買入時機為后一天
- 如果有利潤,則賣出,并且計算利潤
- 再次 - 假定:買入時機(循環步驟 1-3)
4、情侶牽手
N 對情侶坐在連續排列的 2N 個座位上,想要牽到對方的手。計算最少交換座位的次數,以便每對情侶可以并肩坐在一起。一次交換可選擇任意兩人,讓他們站起來交換座位。人和座位用 0 到 2N-1 的整數表示,情侶們按順序編號,第一對是 (0, 1),第二對是 (2, 3),以此類推,最后一對是 (2N-2, 2N-1)。
這些情侶的初始座位 row[i] 是由最初始坐在第 i 個座位上的人決定的。
示例 1:
輸入: row = [0, 2, 1, 3] 輸出: 1 解釋: 我們只需要交換 row[1]和 row[2]的位置即可。
示例 2:
輸入: row = [3, 2, 0, 1] 輸出: 0 解釋: 無需交換座位,所有的情侶都已經可以手牽手了。
- /**
- * @param {number[]} row
- * @return {number}
- */
- var minSwapsCouples = function(row) {
- let hashMap = {}; // {人: 位置}
- for(let i=0; i<row.length; i++){
- hashMap[row[i]] = i
- }
- let ans = 0; // 交換次數
- for(let i=0; i<row.length; i+=2){ // 按照一對遍歷
- let lover=row[i]^1; // row[i]的情侶
- if(hashMap[lover] !== i+1){ // 如果不相鄰,就交換
- ans++;
- hashMap[row[i+1]] = hashMap[lover]; // row[i+1]使用了 lover 的下標
- // 交換位置
- [row[i+1], row[hashMap[lover]]] = [row[hashMap[lover]], row[i+1]]
- hashMap[lover]=i+1; // lover 的下標改為 i+1 使其相鄰
- }
- }
- return ans;
- };
核心思想:
- 遍歷數組,檢查情侶是否相鄰,如果不是,就調整一個的位置使其相鄰。
- 我們盡量只挪動情侶中的一位,另一位不動,這樣才能保證挪動次數最少。
- 這樣交換,不會影響其他的情侶。
代碼解讀:
- 定義函數 minSwapsCouples,接收一個參數 row 即情侶座位關系的數組。
- 得到{人: 位置}的對象。
- 定義交換次數 ans,并在最后將其返回。
- 遍歷左側情侶,檢查右側是否為 TA 的情侶,如果不是,則找到 TA 的情侶并調換座位。
5、參考資料
本文題目來源:力扣(LeetCode)
鏈接:https://leetcode-cn.com
孫領芝: 一個愛好碳水的山東大妞。