求解“微信群覆蓋”的三種方法:暴力,染色,鏈表,并查集
這是一篇聊算法的文章,從一個小面試題開始,擴展到一系列基礎算法,包含幾個部分:
(1) 題目簡介;
(2) 思路一:暴力法;
(3) 思路二:染色法;
(4) 思路三:鏈表法;
(5) 思路四:并查集法。
除了聊方案,重點分享思考過程。文章較長,可提前收藏。
第一部分:題目簡介
問題提出:求微信群覆蓋
微信有很多群,現進行如下抽象:
(1) 每個微信群由一個唯一的gid標識;
(2) 微信群內每個用戶由一個唯一的uid標識;
(3) 一個用戶可以加入多個群;
(4) 群可以抽象成一個由不重復uid組成的集合,例如:
- g1{u1, u2, u3}
- g2{u1, u4, u5}
可以看到,用戶u1加入了g1與g2兩個群。
畫外音:
- gid和uid都是uint64;
- 集合內沒有重復元素;
假設微信有M個群(M為億級別),每個群內平均有N個用戶(N為十級別).
現在要進行如下操作:
(1) 如果兩個微信群中有相同的用戶,則將兩個微信群合并,并生成一個新微信群;
例如,上面的g1和g2就會合并成新的群:
g3{u1, u2, u3, u4, u5};
畫外音:集合g1中包含u1,集合g2中包含u1,合并后的微信群g3也只包含一個u1。
(2) 不斷的進行上述操作,直到剩下所有的微信群都不含相同的用戶為止;
將上述操作稱:求群的覆蓋。
設計算法,求群的覆蓋,并說明算法時間與空間復雜度。
畫外音:你遇到過類似的面試題嗎?
對于一個復雜的問題,思路肯定是“先解決,再優化”,大部分人不是神,很難一步到位。先用一種比較“笨”的方法解決,再看“笨方法”有什么痛點,優化各個痛點,不斷升級方案。
第二部分:暴力法
拿到這個問題,很容易想到的思路是:
(1) 先初始化M個集合,用集合來表示微信群gid與用戶uid的關系;
(2) 找到哪兩個(哪些)集合需要合并;
(3) 接著,進行集合的合并;
(4) 迭代步驟二和步驟三,直至所有集合都沒有相同元素,算法結束;
第一步,如何初始化集合?
set這種數據結構,大家用得很多,來表示集合:
(1) 新建M個set來表示M個微信群gid;
(2) 每個set插入N個元素來表示微信群中的用戶uid;
set有兩種最常見的實現方式,一種是樹型set,一種是哈希型set。
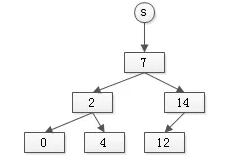
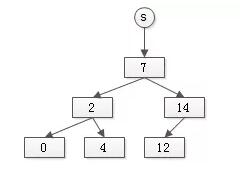
假設有集合:
s={7, 2, 0, 14, 4, 12}
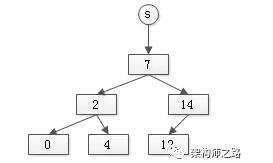
樹型set的實現如下:
其特點是:
- 插入和查找的平均時間復雜度是O(lg(n));
- 能實現有序查找;
- 省空間;
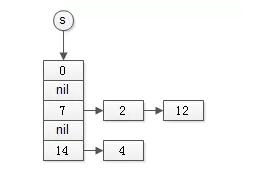
哈希型set實現如下:
其特點是:
- 插入和查找的平均時間復雜度是O(1);
- 不能實現有序查找;
畫外音:求群覆蓋,哈希型實現的初始化更快,復雜度是O(M*N)。
第二步,如何判斷兩個(多個)集合要不要合并?
集合對set(i)和set(j),判斷里面有沒有重復元素,如果有,就需要合并,判重的偽代碼是:
- // 對set(i)和set(j)進行元素判斷并合并
- (1) foreach (element in set(i))
- (2) if (element in set(j))
- merge(set(i), set(j));
第一行(1)遍歷第一個集合set(i)中的所有元素element;
畫外音:這一步的時間復雜度是O(N)。
第二行(2)判斷element是否在第二個集合set(j)中;
畫外音:如果使用哈希型set,第二行(2)的平均時間復雜度是O(1)。
這一步的時間復雜度至少是O(N)*O(1)=O(N)。
第三步,如何合并集合?
集合對set(i)和set(j)如果需要合并,只要把一個集合中的元素插入到另一個集合中即可:
- // 對set(i)和set(j)進行集合合并
- merge(set(i), set(j)){
- (1) foreach (element in set(i))
- (2) set(j).insert(element);
- }
第一行(1)遍歷第一個集合set(i)中的所有元素element;
畫外音:這一步的時間復雜度是O(N)。
第二行(2)把element插入到集合set(j)中;
畫外音:如果使用哈希型set,第二行(2)的平均時間復雜度是O(1)。
這一步的時間復雜度至少是O(N)*O(1)=O(N)。
第四步:迭代第二步與第三步,直至結束
對于M個集合,暴力針對所有集合對,進行重復元素判斷并合并,用兩個for循環可以暴力解決:
- (1)for(i = 1 to M)
- (2) for(j= i+1 to M)
- //對set(i)和set(j)進行元素判斷并合并
- foreach (element in set(i))
- if (element in set(j))
- merge(set(i), set(j));
遞歸調用,兩個for循環,復雜度是O(M*M)。
綜上,如果這么解決群覆蓋的問題,時間復雜度至少是:
- O(M*N) // 集合初始化的過程
- +
- O(M*M) // 兩重for循環遞歸
- *
- O(N) // 判重
- *
- O(N) // 合并
畫外音:實際復雜度要高于這個,隨著集合的合并,集合元素會越來越多,判重和合并的成本會越來越高。
第三部分:染色法
總的來說,暴力法效率非常低,集合都是一個一個合并的,同一個元素在合并的過程中要遍歷很多次。很容易想到一個優化點,能不能一次合并多個集合?
暴力法中,判斷兩個集合se<i>t和set<j>是否需要合并,思路是:遍歷set中的所有element,看在set中是否存在,如果存在,說明存在交集,則需要合并。
哪些集合能夠一次性合并?
當某些集合中包含同一個元素時,可以一次性合并。
怎么一次性發現,哪些集合包含同一個元素,并合并去重呢?
回顧一下工作中的類似需求:
M個文件,每個文件包含N個用戶名,或者N個手機號,如何合并去重?
最常見的玩法是:
- cat file_1 file_2 … file_M | sort | uniq > result
這里的思路是什么?
(1) 把M*N個用戶名/手機號輸出;
(2) sort排序,排序之后相同的元素會相鄰;
(3) uniq去重,相鄰元素如果相同只保留一個;
“排序之后相同的元素會相鄰”,就是一次性找出所有可合并集合的關鍵,這是染色法的核心。
舉一個栗子:
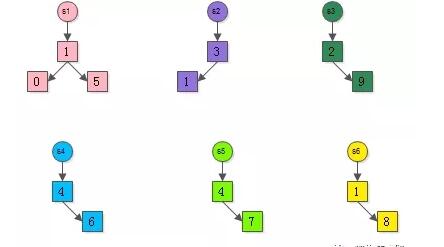
假設有6個微信群,每個微信群有若干個用戶:
- s1={1,0,5} s2={3,1} s3={2,9}
- s4={4,6} s5={4,7} s6={1,8}
假設使用樹形set來表示集合。
首先,給同一個集合中的所有元素染上相同的顏色,表示來自同一個集合。
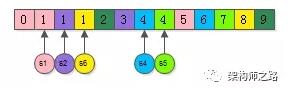
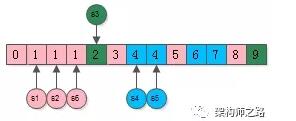
然后,對所有的元素進行排序,會發現:
(1) 相同的元素一定相鄰,并且一定來自不同的集合;
(2) 同一個顏色的元素被打散了;
這些相鄰且相同的元素,來自哪一個集合,這些集合就是需要合并的,如上圖:
(1) 粉色的1來自集合s1,紫色的1來自集合s2,黃色的1來自集合s6,所以s1s2s6需要合并;
(2) 藍色的4來自集合s4,青色的4來自集合s5,所以s4s5需要合并;
不用像暴力法遍歷所有的集合對,而是一個排序動作,就能找到所有需要合并的集合。
畫外音:暴力法一次處理2個集合,染色法一次可以合并N個集合。
集合合并的過程,可以想象為,相同相鄰元素所在集合,染成第一個元素的顏色:
(1) 紫色和黃色,染成粉色;
(2) 青色,染成藍色;
最終,剩余三種顏色,也就是三個集合:
- s1={0,1,3,5,8}
- s3={2,9}
- s4={4,6,7}
神奇不神奇!!!
染色法有意思么?但仍有兩個遺留問題:
(1) 粉色1,紫色1,黃色1,三個元素如何找到這三個元素所在的集合s1s2s6呢?
(2) s1s2s6三個集合如何快速合并?
畫外音:假設總元素個數n=M*N,如果使用樹形set,合并的復雜度為O(n*lg(n)),即O(M*N*lg(M*N))。
我們繼續往下看。
第四部分:鏈表法
染色法遺留了兩個問題:
- 步驟(2)中,如何通過元素快速定位集合?
- 步驟(3)中,如何快速合并集合?
我們繼續聊聊這兩個問題的優化思路。
問題一:如何由元素快速定位集合?
普通的集合,只能由集合根(root)定位元素,不能由元素逆向定位root,如何支持元素逆向定位root呢?
很容易想到,每個節點增加一個父指針即可。
更具體的:
- element{
- int data;
- element* left;
- element* right;
- }
升級為:
- element{
- element* parent; // 指向父節點
- int data;
- element* left;
- element* right;
- }
如上圖:所有節點的parent都指向它的上級,而只有root->parent=NULL。
對于任意一個元素,找root的過程為:
- element* X_find_set_root(element* x){
- element* temp=x;
- while(temp->parent != NULL){
- temptemp= temp->parent;
- }
- return temp;
- }
很容易發現,由元素找集合根的時間復雜度是樹的高度,即O(lg(n))。
有沒有更快的方法呢?
進一步思考,為什么每個節點要指向父節點,直接指向根節點是不是也可以。
更具體的:
- element{
- int data;
- element* left;
- element* right;
- }
升級為:
- element{
- element* root; // 指向集合根
- int data;
- element* left;
- element* right;
- }
如上圖:所有節點的parent都指向集合的根。
對于任意一個元素,找root的過程為:
- element* X_find_set_root(element* x){
- return x->root;
- }
很容易發現,升級后,由元素找集合根的時間復雜度是O(1)。
畫外音:不能更快了吧。
另外,這種方式,能在O(1)的時間內,判斷兩個元素是否在同一個集合內:
- bool in_the_same_set(element* a, element* b){
- return (a->root == b->root);
- }
甚為方便。
畫外音:兩個元素的根相同,就在同一個集合內。
問題二:如何快速進行集合合并?
暴力法中提到過,集合合并的偽代碼為:
- merge(set(i), set(j)){
- foreach(element in set(i))
- set(j).insert(element);
- }
把一個集合中的元素插入到另一個集合中即可。
假設set(i)的元素個數為n1,set(j)的元素個數為n2,其時間復雜度為O(n1*lg(n2))。
在“微信群覆蓋”這個業務場景下,隨著集合的不斷合并,集合高度越來越高,合并會越來越慢,有沒有更快的集合合并方式呢?
仔細回顧一下:
(1) 樹形set的優點是,支持有序查找,省空間;
(2) 哈希型set的優點是,快速插入與查找;
而“微信群覆蓋”場景對集合的頻繁操作是:
(1) 由元素找集合根;
(2) 集合合并;
那么,為什么要用樹形結構或者哈希型結構來表示集合呢?
畫外音:優點完全沒有利用上嘛。
讓我們來看看,這個場景中,如果用鏈表來表示集合會怎么樣,合并會不會更快?
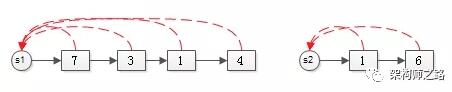
- s1={7,3,1,4}
- s2={1,6}
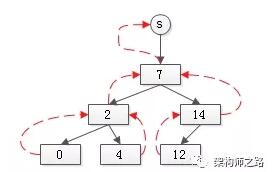
如上圖,分別用鏈表來表示這兩個集合。可以看到,為了滿足“快速由元素定位集合根”的需求,每個元素仍然會指向根。
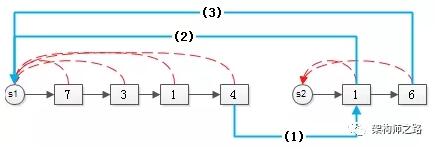
s1和s2如果要合并,需要做兩件事:
- 集合1的尾巴,鏈向集合2的頭(藍線1);
- 集合2的所有元素,指向集合1的根(藍線2,3);
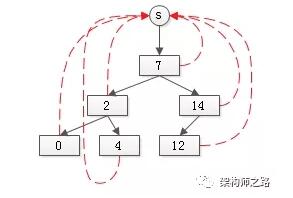
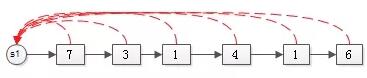
合并完的效果是:
變成了一個更大的集合。
假設set(1)的元素個數為n1,set(2)的元素個數為n2,整個合并的過程的時間復雜度是O(n2)。
畫外音:時間耗在set(2)中的元素變化。
咦,我們發現:
(1) 將短的鏈表,接到長的鏈表上;
(2) 將長的鏈表,接到短的鏈表上;
所使用的時間是不一樣的。
為了讓時間更快,一律使用更快的方式:“元素少的鏈表”主動接入到“元素多的鏈表”的尾巴后面。這樣,改變的元素個數能更少一些,這個優化被稱作“加權合并”。
對于M個微信群,平均每個微信群N個用戶的場景,用鏈表的方式表示集合,按照“加權合并”的方式合并集合,最壞的情況下,時間復雜度是O(M*N)。
畫外音:假設所有的集合都要合并,共M次,每次都要改變N個元素的根指向,故為O(M*N)。
于是,對于“M個群,每個群N個用戶,微信群求覆蓋”問題,使用“染色法”加上“鏈表法”,核心思路三步驟:
(1) 全部元素全局排序;
(2) 全局排序后,不同集合中的相同元素,一定是相鄰的,通過相同相鄰的元素,一次性找到所有需要合并的集合;
(3) 合并這些集合,算法完成;
其中:
- 步驟(1),全局排序,時間復雜度O(M*N);
- 步驟(2),染色思路,能夠迅猛定位哪些集合需要合并,每個元素增加一個屬性指向集合根,實現O(1)級別的元素定位集合;
- 步驟(3),使用鏈表表示集合,使用加權合并的方式來合并集合,合并的時間復雜度也是O(M*N);
總時間復雜度是:
- O(M*N) //排序
- +
- O(1) //由元素找到需要合并的集合
- *
- O(M*N) //集合合并
神奇不神奇!!!
神奇不止一種,還有其他方法嗎?我們接著往下看。
第五部分:并查集法
分離集合(disjoint set)是一種經典的數據結構,它有三類操作:
- Make-set(a):生成一個只有一個元素a的集合;
- Union(X, Y):合并兩個集合X和Y;
- Find-set(a):查找元素a所在集合,即通過元素找集合;
這種數據結構特別適合用來解決這類集合合并與查找的問題,又稱為并查集。
能不能利用并查集來解決求“微信群覆蓋”問題呢?
一、并查集的鏈表實現
鏈表法里基本聊過,為了保證知識的系統性,這里再稍微回顧一下。
如上圖,并查集可以用鏈表來實現。
鏈表實現的并查集,Find-set(a)的時間復雜度是多少?
集合里的每個元素,都指向“集合的句柄”,這樣可以使得“查找元素a所在集合S”,即Find-set(a)操作在O(1)的時間內完成。
鏈表實現的并查集,Union(X, Y)的時間復雜度是多少?
假設有集合:
- S1={7,3,1,4}
- S2={1,6}
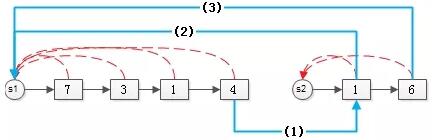
合并S1和S2兩個集合,需要做兩件事情:
(1) 第一個集合的尾元素,鏈向第二個集合的頭元素(藍線1);
(2) 第二個集合的所有元素,指向第一個集合的句柄(藍線2,3);
合并完的效果是:
變成了一個更大的集合S1。
集合合并時,將短的鏈表,往長的鏈表上接,這樣變動的元素更少,這個優化叫做“加權合并”。
畫外音:實現的過程中,集合句柄要存儲元素個數,頭元素,尾元素等屬性,以方便上述操作進行。
假設每個集合的平均元素個數是n,Union(X, Y)操作的時間復雜度是O(n)。
能不能Find-set(a)與Union(X, Y)都在O(1)的時間內完成呢?
可以,這就引發了并查集的第二種實現方法。
二、并查集的有根樹實現
什么是有根樹,和普通的樹有什么不同?
常用的set,就是用普通的二叉樹實現的,其元素的數據結構是:
- element{
- int data;
- element* left;
- element* right;
- }
通過左指針與右指針,父親節點指向兒子節點。
而有根樹,其元素的數據結構是:
- element{
- int data;
- element* parent;
- }
通過兒子節點,指向父親節點。
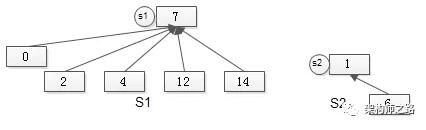
假設有集合:
- S1={7,3,1,4}
- S2={1,6}
通過如果通過有根樹表示,可能是這樣的:
所有的元素,都通過parent指針指向集合句柄,所有元素的Find-set(a)的時間復雜度也是O(1)。
畫外音:假設集合的首個元素,代表集合句柄。
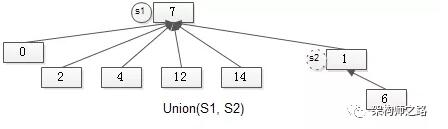
有根樹實現的并查集,Union(X, Y)的過程如何?時間復雜度是多少?
通過有根樹實現并查集,集合合并時,直接將一個集合句柄,指向另一個集合即可。
如上圖所示,S2的句柄,指向S1的句柄,集合合并完成:S2消亡,S1變為了更大的集合。
容易知道,集合合并的時間復雜度為O(1)。
會發現,集合合并之后,有根樹的高度變高了,與“加權合并”的優化思路類似,總是把節點數少的有根樹,指向節點數多的有根樹(更確切的說,是高度矮的樹,指向高度高的樹),這個優化叫做“按秩合并”。
新的問題來了,集合合并之后,不是所有元素的Find-set(a)操作都是O(1)了,怎么辦?
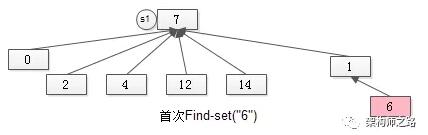
如圖S1與S2合并后的新S1,首次“通過元素6來找新S1的句柄”,不能在O(1)的時間內完成了,需要兩次操作。
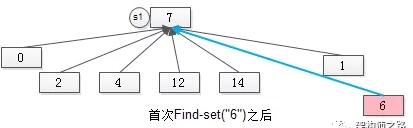
但為了讓未來“通過元素6來找新S1的句柄”的操作能夠在O(1)的時間內完成,在首次進行Find-set(“6”)時,就要將元素6“尋根”路徑上的所有元素,都指向集合句柄,如下圖。
某個元素如果不直接指向集合句柄,首次Find-set(a)操作的過程中,會將該路徑上的所有元素都直接指向句柄,這個優化叫做“路徑壓縮”。
畫外音:路徑上的元素第二次執行Find-set(a)時,時間復雜度就是O(1)了。
實施“路徑壓縮”優化之后,Find-set的平均時間復雜度仍是O(1)。
稍微總結一下。
通過鏈表實現并查集:
(1) Find-set的時間復雜度,是O(1)常數時間;
(2) Union的時間復雜度,是集合平均元素個數,即線性時間;
畫外音:別忘了“加權合并”優化。
通過有根樹實現并查集:
(1) Union的時間復雜度,是O(1)常數時間;
(2) Find-set的時間復雜度,通過“按秩合并”與“路徑壓縮”優化后,平均時間復雜度也是O(1);
即,使用并查集,非常適合解決“微信群覆蓋”問題。
知其然,知其所以然,思路往往比結果更重要。
算法,其實還是挺有意思的。
【本文為51CTO專欄作者“58沈劍”原創稿件,轉載請聯系原作者】