面試官:請說出四種不使用第三方變量交換兩個變量值的方法
哈嘍,大家好,我是阿Q。前幾天有個小伙伴去面試,被面試官的一個問題勸退了:請說出幾種不使用第三方變量交換兩個變量值的方法。
問題有點繞,好不容易縷清了面試官的問題,卻發現答不上來。一時間尷尬無比,只能硬著頭皮說不會。
遇到交換變量值的問題,通常我們的做法是:定義一個新的變量,借助它完成交換。
代碼如下:
- t = a;
- a = b;
- b = t;
但問題的重點是“不使用第三方變量”,那就變得“可愛”起來了。思考過后,拋出以下四種方法來解決該問題:
- 變量本身交換數值;
- 算術運算;
- 指針地址操作;
- 位運算;
變量本身交換數值
- b = (a + b) - (a = b);
首先執行 a + b 操作,然后將 b 賦值給 a,則 b = a + b - b = a,這就完成了 ab 的互換操作。
算術運算
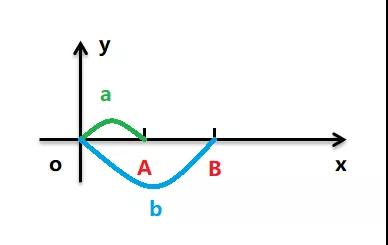
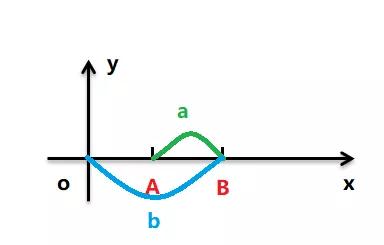
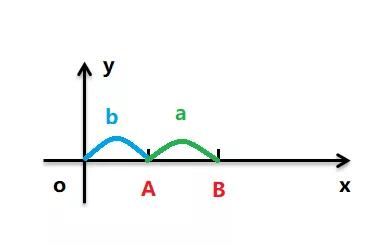
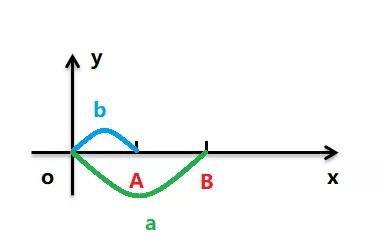
如圖所示:OA = a; OB = b; AB = b - a;
首先我們把 AB 之間的距離 b - a 賦值給 a,此時 AB = a, OB = b 。
由于要達到 ab 交換的目的,所以 OA 要等于 b,而此時 OA 的距離為 b - a ,所以得將 b - a 賦值給 b ,此時 OA = b, AB = a 。
很容易從圖中看出,OB 的距離為 b + a,所以我們只需要將 b + a 賦值給 a 就可以完成兩者的交換了。
綜上所述,我們的步驟為
- int a = 10;
- int b = 15;
- a = b - a; //b=15;a=5;
- b = b - a; //b=10;a=5;
- a = b + a; //b=10;a=15;
該算法只能用于整型類型。
指針地址操作
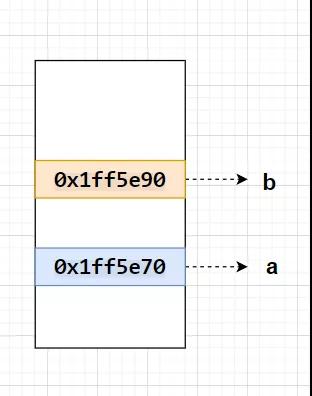
我們可以把 a 和 b 想象為內存中的地址值,假設 a 為 0x01ff5e70 ,b 為 0x01ff5e90 ,而 b - a 表示兩個變量在內存中的儲存位置隔了多少個字節。所以我們理論上也可以按算術運算的邏輯來交換兩個變量的值。
代碼如下(此處是 c 語言):
- //其中 a 和 b 都是指針變量,里邊存儲著10和20的地址
- int *a = new int(10); //a=0x01ff5e70 ,此處代表a中存儲的地址
- int *b = new int(20); //b=0x01ff5e90 ,此處代表b中存儲的地址
- //指針變量相減得到20和10的地址間隔了多少個字節,然后轉為指針變量
- a = (int*)(b-a); //b=0x01ff5e90;a=0x8
- b = (int*)(b-a); //b=0x01ff5e70;a=0x8
- a=(int*)(b+long(a));//b=0x01ff5e70;a=0x01ff5e90
b - a = 0x01ff5e90 - 0x01ff5e70 = 0x20,0x20 轉換為十進制為 32 位,因為一個 int 占4位,所以這里是 0x8 。
以上只是理論狀態下的執行過程,如果直接執行是不能實現交換的。因為上邊的代碼忽略了一個問題:代碼編譯之后,變量都是存在內存中的,而內存區都會存在基地址。
基地址可以理解為某塊內存的起點。上邊的數據都是在基地址的基礎上做了偏移。
變量的地址 = 變量的基地址 + 變量的偏移地址
當我們進行 b - a 操作的時候,得到結果為 8 ,然后轉化為指針變量的時候就會給 8 自動添加基地址,此時的結果就不是 0x8 了,所以會導致結果錯誤。
另外,地址運算不能出現負數,即當 a 的地址大于 b 的地址時,b - a < 0 ,系統自動采用補碼的形式表示負的位移,也會產生錯誤。
為了解決這個問題,我們只需要保證 b - a 得到的結果不受基地址的影響即可,所以給出以下解決方案。
- int *a = new int(10);
- int *b = new int(20);
- cout << a << "`````";
- cout << b << "`````";
- if(a < b){
- a = (int*)(b-a);
- cout << a << "`````";
- b=(int*)(b-(long(a)&0x0000ffff));
- cout << b << "`````";
- a=(int*)(b+long(a));
- cout << a << "`````";
- } else {
- b = (int*)(a-b);
- cout << b << "`````";
- a=(int*)(a-(long(b)&0x0000ffff));
- cout << a << "`````";
- b=(int*)(a+long(b));
- cout << b << "`````";
- }
執行結果:
- 0x8dbe70`````0x8dbe90`````0x8`````0x8dbe70`````0x8dbe90`````
看到這,不知道大家是否真的看懂了。反正我第一次看到這兒時,感覺非常清晰(其實完全沒有理解),第二次看的時候懵逼了,完全不懂,所以還得大家仔細思考一下才行。
b=(int*)(b-(long(a)&0x0000ffff)); 指令的精妙之處就在于采用了位運算中的與運算,將 a 和 0x0000ffff 進行與運算后,b - a 的基地址計算結果被屏蔽,只保留了偏移地址的計算結果,也就是我們需要的字節數。
在交換很大的數據類型時,該方法執行速度比算術算法快。因為它交換的是地址,而變量值在內存中是沒有移動過的。
位運算
既然上邊用到了位運算,那我們再說一種直接通過“異或“完成交換的方法。
簡單介紹一下異或的規則:
- 如果a、b兩個值不相同,則異或結果為1;
- 如果a、b兩個值相同,異或結果為0。
代碼如下
- int a=10, b=12;//二進制:a=1010;b=1100;
- a = a^b;//a=0110;b=1100
- b = a^b;//a=0110;b=1010
- a = a^b;//a=1100;b=1010
- System.out.println("a="+ a +",b="+ b);
執行結果
- a=12,b=10
異或運算能夠使數據中的某些位翻轉,其他位不變。這就意味著任意一個數與任意一個給定的值連續異或兩次,值不變。
簡單總結
以上四種方法均實現了不借助第三方變量來完成兩個變量值的交換:
- 算術運算和位運算計算量相當,只能進行整形數據的交換;
- 地址運算中計算較復雜,可以很輕松的實現大類型(比如自定義的類或結構)的交換;
- 理論上重載 “^” 運算符,也可以實現任意結構的交換;
以上就是今天的全部內容了,如果你有不同的意見或者更好的idea,歡迎聯系阿Q,添加阿Q可以加入技術交流群參與討論呦!
本文轉載自微信公眾號「阿Q說代碼」,可以通過以下二維碼關注。轉載本文請聯系阿Q說代碼公眾號。