一篇帶你了解DP入門之爬樓梯
爬樓梯
力扣題目鏈接:https://leetcode-cn.com/problems/climbing-stairs
假設(shè)你正在爬樓梯。需要 n 階你才能到達(dá)樓頂。
每次你可以爬 1 或 2 個(gè)臺(tái)階。你有多少種不同的方法可以爬到樓頂呢?
注意:給定 n 是一個(gè)正整數(shù)。
示例 1:
- 輸入:2
- 輸出:2
- 解釋:有兩種方法可以爬到樓頂。
- 1 階 + 1 階
- 2 階
示例 2:
- 輸入:3
- 輸出:3
- 解釋:有三種方法可以爬到樓頂。
- 1 階 + 1 階 + 1 階
- 1 階 + 2 階
- 2 階 + 1 階
思路
本題大家如果沒(méi)有接觸過(guò)的話,會(huì)感覺(jué)比較難,多舉幾個(gè)例子,就可以發(fā)現(xiàn)其規(guī)律。
爬到第一層樓梯有一種方法,爬到二層樓梯有兩種方法。
那么第一層樓梯再跨兩步就到第三層 ,第二層樓梯再跨一步就到第三層。
所以到第三層樓梯的狀態(tài)可以由第二層樓梯 和 到第一層樓梯狀態(tài)推導(dǎo)出來(lái),那么就可以想到動(dòng)態(tài)規(guī)劃了。
我們來(lái)分析一下,動(dòng)規(guī)五部曲:
定義一個(gè)一維數(shù)組來(lái)記錄不同樓層的狀態(tài)
確定dp數(shù)組以及下標(biāo)的含義
dp[i]:爬到第i層樓梯,有dp[i]種方法
確定遞推公式
如果可以推出dp[i]呢?
從dp[i]的定義可以看出,dp[i] 可以有兩個(gè)方向推出來(lái)。
首先是dp[i - 1],上i-1層樓梯,有dp[i - 1]種方法,那么再一步跳一個(gè)臺(tái)階不就是dp[i]了么。
還有就是dp[i - 2],上i-2層樓梯,有dp[i - 2]種方法,那么再一步跳兩個(gè)臺(tái)階不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]與dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推導(dǎo)dp[i]的時(shí)候,一定要時(shí)刻想著dp[i]的定義,否則容易跑偏。
這體現(xiàn)出確定dp數(shù)組以及下標(biāo)的含義的重要性!
dp數(shù)組如何初始化
在回顧一下dp[i]的定義:爬到第i層樓梯,有dp[i]中方法。
那么i為0,dp[i]應(yīng)該是多少呢,這個(gè)可以有很多解釋,但都基本是直接奔著答案去解釋的。
例如強(qiáng)行安慰自己爬到第0層,也有一種方法,什么都不做也就是一種方法即:dp[0] = 1,相當(dāng)于直接站在樓頂。
但總有點(diǎn)牽強(qiáng)的成分。
那還這么理解呢:我就認(rèn)為跑到第0層,方法就是0啊,一步只能走一個(gè)臺(tái)階或者兩個(gè)臺(tái)階,然而樓層是0,直接站樓頂上了,就是不用方法,dp[0]就應(yīng)該是0.
其實(shí)這么爭(zhēng)論下去沒(méi)有意義,大部分解釋說(shuō)dp[0]應(yīng)該為1的理由其實(shí)是因?yàn)閐p[0]=1的話在遞推的過(guò)程中i從2開始遍歷本題就能過(guò),然后就往結(jié)果上靠去解釋dp[0] = 1。
從dp數(shù)組定義的角度上來(lái)說(shuō),dp[0] = 0 也能說(shuō)得通。
需要注意的是:題目中說(shuō)了n是一個(gè)正整數(shù),題目根本就沒(méi)說(shuō)n有為0的情況。
所以本題其實(shí)就不應(yīng)該討論dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,這個(gè)初始化大家應(yīng)該都沒(méi)有爭(zhēng)議的。
所以我的原則是:不考慮dp[0]如果初始化,只初始化dp[1] = 1,dp[2] = 2,然后從i = 3開始遞推,這樣才符合dp[i]的定義。
確定遍歷順序
從遞推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍歷順序一定是從前向后遍歷的
舉例推導(dǎo)dp數(shù)組
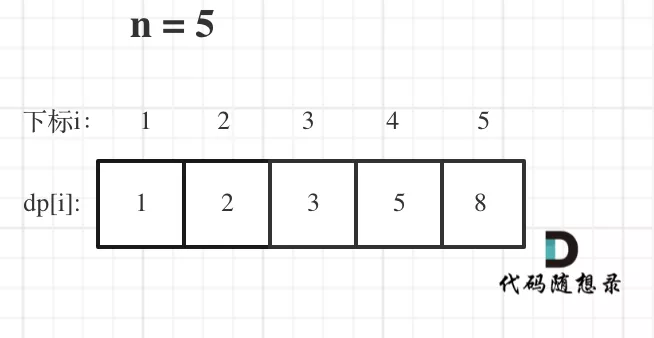
舉例當(dāng)n為5的時(shí)候,dp table(dp數(shù)組)應(yīng)該是這樣的
爬樓梯
如果代碼出問(wèn)題了,就把dp table 打印出來(lái),看看究竟是不是和自己推導(dǎo)的一樣。
此時(shí)大家應(yīng)該發(fā)現(xiàn)了,這不就是斐波那契數(shù)列么!
唯一的區(qū)別是,沒(méi)有討論dp[0]應(yīng)該是什么,因?yàn)閐p[0]在本題沒(méi)有意義!
以上五部分析完之后,C++代碼如下:
- // 版本一
- class Solution {
- public:
- int climbStairs(int n) {
- if (n <= 1) return n; // 因?yàn)橄旅嬷苯訉?duì)dp[2]操作了,防止空指針
- vector<int> dp(n + 1);
- dp[1] = 1;
- dp[2] = 2;
- for (int i = 3; i <= n; i++) { // 注意i是從3開始的
- dp[i] = dp[i - 1] + dp[i - 2];
- }
- return dp[n];
- }
- };
- 時(shí)間復(fù)雜度:
- 空間復(fù)雜度:
當(dāng)然依然也可以,優(yōu)化一下空間復(fù)雜度,代碼如下:
- // 版本二
- class Solution {
- public:
- int climbStairs(int n) {
- if (n <= 1) return n;
- int dp[3];
- dp[1] = 1;
- dp[2] = 2;
- for (int i = 3; i <= n; i++) {
- int sum = dp[1] + dp[2];
- dp[1] = dp[2];
- dp[2] = sum;
- }
- return dp[2];
- }
- };
- 時(shí)間復(fù)雜度:
- 空間復(fù)雜度:
后面將講解的很多動(dòng)規(guī)的題目其實(shí)都是當(dāng)前狀態(tài)依賴前兩個(gè),或者前三個(gè)狀態(tài),都可以做空間上的優(yōu)化,但我個(gè)人認(rèn)為面試中能寫出版本一就夠了哈,清晰明了,如果面試官要求進(jìn)一步優(yōu)化空間的話,我們?cè)偃?yōu)化。
因?yàn)榘姹疽徊拍荏w現(xiàn)出動(dòng)規(guī)的思想精髓,遞推的狀態(tài)變化。
拓展
這道題目還可以繼續(xù)深化,就是一步一個(gè)臺(tái)階,兩個(gè)臺(tái)階,三個(gè)臺(tái)階,直到 m個(gè)臺(tái)階,有多少種方法爬到n階樓頂。
這又有難度了,這其實(shí)是一個(gè)完全背包問(wèn)題,但力扣上沒(méi)有這種題目,所以后續(xù)我在講解背包問(wèn)題的時(shí)候,今天這道題還會(huì)拿從背包問(wèn)題的角度上來(lái)再講一遍。
這里我先給出我的實(shí)現(xiàn)代碼:
- class Solution {
- public:
- int climbStairs(int n) {
- vector<int> dp(n + 1, 0);
- dp[0] = 1;
- for (int i = 1; i <= n; i++) {
- for (int j = 1; j <= m; j++) { // 把m換成2,就可以AC爬樓梯這道題
- if (i - j >= 0) dp[i] += dp[i - j];
- }
- }
- return dp[n];
- }
- };
代碼中m表示最多可以爬m(xù)個(gè)臺(tái)階。
以上代碼不能運(yùn)行哈,我主要是為了體現(xiàn)只要把m換成2,粘過(guò)去,就可以AC爬樓梯這道題,不信你就粘一下試試,哈哈。
此時(shí)我就發(fā)現(xiàn)一個(gè)絕佳的大廠面試題,第一道題就是單純的爬樓梯,然后看候選人的代碼實(shí)現(xiàn),如果把dp[0]的定義成1了,就可以發(fā)難了,為什么dp[0]一定要初始化為1,此時(shí)可能候選人就要強(qiáng)行給dp[0]應(yīng)該是1找各種理由。那這就是一個(gè)考察點(diǎn)了,對(duì)dp[i]的定義理解的不深入。
然后可以繼續(xù)發(fā)難,如果一步一個(gè)臺(tái)階,兩個(gè)臺(tái)階,三個(gè)臺(tái)階,直到 m個(gè)臺(tái)階,有多少種方法爬到n階樓頂。這道題目leetcode上并沒(méi)有原題,絕對(duì)是考察候選人算法能力的絕佳好題。
這一連套問(wèn)下來(lái),候選人算法能力如何,面試官心里就有數(shù)了。
其實(shí)大廠面試最喜歡問(wèn)題的就是這種簡(jiǎn)單題,然后慢慢變化,在小細(xì)節(jié)上考察候選人。
總結(jié)
這道題目和動(dòng)態(tài)規(guī)劃:斐波那契數(shù)題目基本是一樣的,但是會(huì)發(fā)現(xiàn)本題相比動(dòng)態(tài)規(guī)劃:斐波那契數(shù)難多了,為什么呢?
關(guān)鍵是 動(dòng)態(tài)規(guī)劃:斐波那契數(shù) 題目描述就已經(jīng)把動(dòng)規(guī)五部曲里的遞歸公式和如何初始化都給出來(lái)了,剩下幾部曲也自然而然的推出來(lái)了。
而本題,就需要逐個(gè)分析了,大家現(xiàn)在應(yīng)該初步感受出關(guān)于動(dòng)態(tài)規(guī)劃,你該了解這些!里給出的動(dòng)規(guī)五部曲了。
簡(jiǎn)單題是用來(lái)掌握方法論的,例如昨天斐波那契的題目夠簡(jiǎn)單了吧,但昨天和今天可以使用一套方法分析出來(lái)的,這就是方法論!
所以不要輕視簡(jiǎn)單題,那種憑感覺(jué)就刷過(guò)去了,其實(shí)和沒(méi)掌握區(qū)別不大,只有掌握方法論并說(shuō)清一二三,才能觸類旁通,舉一反三哈!
就醬,循序漸進(jìn)學(xué)算法,認(rèn)準(zhǔn)「代碼隨想錄」!
其他語(yǔ)言版本
Java
- class Solution {
- public int climbStairs(int n) {
- // 跟斐波那契數(shù)列一樣
- if(n <= 2) return n;
- int a = 1, b = 2, sum = 0;
- for(int i = 3; i <= n; i++){
- sum = a + b;
- a = b;
- b = sum;
- }
- return b;
- }
- }
- // 常規(guī)方式
- public int climbStairs(int n) {
- int[] dp = new int[n + 1];
- dp[0] = 1;
- dp[1] = 1;
- for (int i = 2; i <= n; i++) {
- dp[i] = dp[i - 1] + dp[i - 2];
- }
- return dp[n];
- }
- // 用變量記錄代替數(shù)組
- public int climbStairs(int n) {
- int a = 0, b = 1, c = 0; // 默認(rèn)需要1次
- for (int i = 1; i <= n; i++) {
- c = a + b; // f(i - 1) + f(n - 2)
- a = b; // 記錄上一輪的值
- b = c; // 向后步進(jìn)1個(gè)數(shù)
- }
- return c;
- }
Python
- class Solution:
- def climbStairs(self, n: int) -> int:
- # dp[i]表示爬到第i級(jí)樓梯的種數(shù), (1, 2) (2, 1)是兩種不同的類型
- dp = [0] * (n + 1)
- dp[0] = 1
- for i in range(n+1):
- for j in range(1, 3):
- if i>=j:
- dp[i] += dp[i-j]
- return dp[-1]
Go
- func climbStairs(n int) int {
- if n==1{
- return 1
- }
- dp:=make([]int,n+1)
- dp[1]=1
- dp[2]=2
- for i:=3;i<=n;i++{
- dp[i]=dp[i-1]+dp[i-2]
- }
- return dp[n]
- }
Javascript
- var climbStairs = function(n) {
- // dp[i] 為第 i 階樓梯有多少種方法爬到樓頂
- // dp[i] = dp[i - 1] + dp[i - 2]
- let dp = [1 , 2]
- for(let i = 2; i < n; i++) {
- dp[i] = dp[i - 1] + dp[i - 2]
- }
- return dp[n - 1]
- };