本文轉載自微信公眾號「神光的編程秘籍」，作者神說要有光。轉載本文請聯系神光的編程秘籍公眾號。

TS 類型體操小冊掘金排期到 4月份了，有點晚。。。

所以，我把其中一個套路提出來作為文章發了，大家可以提前感受下，到時候也會設置為小冊的試讀章節。

這個套路叫做數組長度做計數，就是用數組長度實現加減乘除、各種計數，是六大套路里最騷的一個。

下面是正文(小冊原文)：

套路四：數組長度做計數

TypeScript 類型系統不是圖靈完備，各種邏輯都能寫么，但好像沒發現數值相關的邏輯。

沒錯，數值相關的邏輯比較繞，被我單獨摘了出來，就是這節要講的內容。

這是類型體操的第四個套路：數組長度做計數。

數組長度做計數

TypeScript 類型系統沒有加減乘除運算符，怎么做數值運算呢?

不知道大家有沒有注意到數組類型取 length 就是數值。

比如：

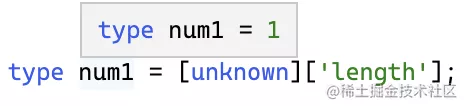
而數組類型我們是能構造出來的，那么通過構造不同長度的數組然后取 length，不就是數值的運算么?

TypeScript 類型系統中沒有加減乘除運算符，但是可以通過構造不同的數組然后取 length 的方式來完成數值計算，把數值的加減乘除轉化為對數組的提取和構造。

這點可以說是類型體操中最麻煩的一個點，需要思維做一些轉換，繞過這個彎來。

下面我們就來做一些真實的案例來掌握它吧。

數組長度實現加減乘除

Add

我們知道了數值計算要轉換為對數組類型的操作，那么加法的實現很容易想到：

構造兩個數組，然后合并成一個，取 length。

比如 3 + 2，就是構造一個長度為 3 的數組類型，再構造一個長度為 2 的數組類型，然后合并成一個數組，取 length。

構造多長的數組是不確定的，需要遞歸構造，這個我們實現過：

type BuildArray<
    Length extends number, 
    Ele = unknown, 
    Arr extends unknown[] = []
> = Arr['length'] extends Length 
        ? Arr 
        : BuildArray<Length, Ele, [...Arr, Ele]>;

類型參數 Length 是要構造的數組的長度。類型參數 Ele 是數組元素，默認為 unknown。類型參數 Arr 為構造出的數組，默認是 []。

如果 Arr 的長度到達了 Length，就返回構造出的 Arr，否則繼續遞歸構造。

構造數組實現了，那么基于它就能實現加法：

type Add<Num1 extends number, Num2 extends number> = 
    [...BuildArray<Num1>,...BuildArray<Num2>]['length'];

我們拿大一點的數測試下：

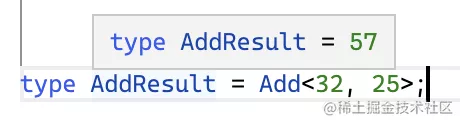
結果是對的。

就這樣，我們通過構造一定長度的數組取 length 的方式實現了加法運算。

Subtract

加法是構造數組，那減法怎么做呢?

減法是從數值中去掉一部分，很容易想到可以通過數組類型的提取來做。

比如 3 是 [unknown, unknown, unknown] 的數組類型，提取出 2 個元素之后，剩下的數組再取 length 就是 1。

所以減法的實現是這樣的：

type Subtract<Num1 extends number, Num2 extends number> = 
    BuildArray<Num1> extends [...arr1: BuildArray<Num2>, ...arr2: infer Rest]
        ? Rest['length']
        : never;

類型參數 Num1、Num2 分別是被減數和減數，通過 extends 約束為 number。

構造 Num1 長度的數組，通過模式匹配提取出 Num2 長度個元素，剩下的放到 infer 聲明的局部變量 Rest 里。

取 Rest 的長度返回，就是減法的結果。

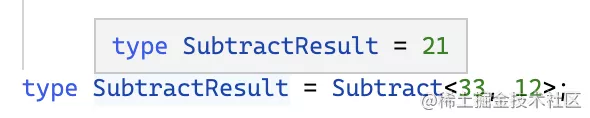
就這樣，我們通過數組類型的提取實現了減法運算。

Multiply

我們把加法轉換為了數組構造，把減法轉換為了數組提取。那乘法怎么做呢?

為了解釋乘法，我去翻了下小學教材，找到了這樣一張圖：

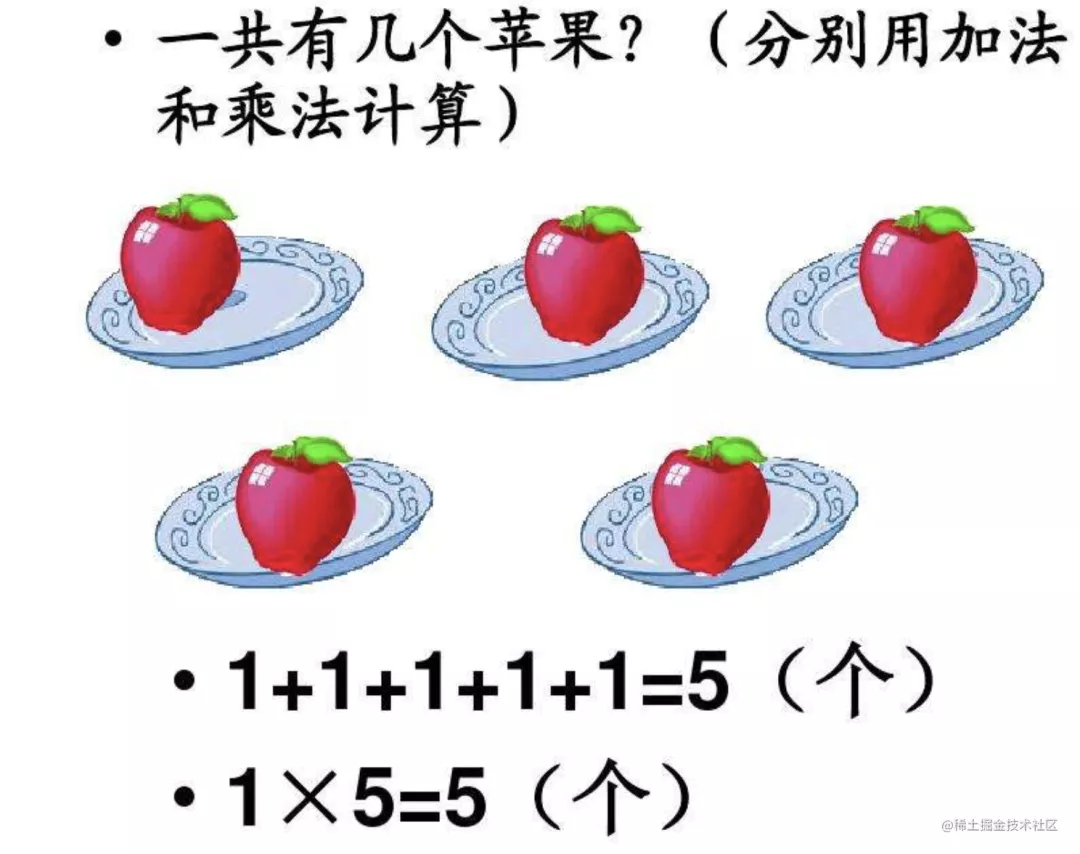
1 乘以 5 就相當于 1 + 1 + 1 + 1 + 1，也就是說乘法就是多個加法結果的累加。

那么我們在加法的基礎上，多加一個參數來傳遞中間結果的數組，算完之后再取一次 length 就能實現乘法：

type Mutiply<
    Num1 extends number,
    Num2 extends number,
    ResultArr extends unknown[] = []
> = Num2 extends 0 ? ResultArr['length']
        : Mutiply<Num1, Subtract<Num2, 1>, [...BuildArray<Num1>, ...ResultArr]>;

類型參數 Num1 和 Num2 分別是被加數和加數。

因為乘法是多個加法結果的累加，我們加了一個類型參數 ResultArr 來保存中間結果，默認值是 []，相當于從 0 開始加。

每加一次就把 Num2 減一，直到 Num2 為 0，就代表加完了。

加的過程就是往 ResultArr 數組中放 Num1 個元素。

這樣遞歸的進行累加，也就是遞歸的往 ResultArr 中放元素。

最后取 ResultArr 的 length 就是乘法的結果。

就這樣，我們通過遞歸的累加實現了乘法。

Divide

乘法是遞歸的累加，那減法不就是遞歸的累減么?

我再去翻了下小學教材，找到了這樣一張圖：

我們有 9 個蘋果，分給美羊羊 3 個，分給懶羊羊 3 個，分給沸羊羊 3 個，最后剩下 0 個。所以 9 / 3 = 3。

所以，除法的實現就是被減數不斷減去減數，直到減為 0，記錄減了幾次就是結果。

也就是這樣的：

type Divide<
    Num1 extends number,
    Num2 extends number,
    CountArr extends unknown[] = []
> = Num1 extends 0 ? CountArr['length']
        : Divide<Subtract<Num1, Num2>, Num2, [unknown, ...CountArr]>;

類型參數 Num1 和 Num2 分別是被減數和減數。

類型參數 CountArr 是用來記錄減了幾次的累加數組。

如果 Num1 減到了 0 ，那么這時候減了幾次就是除法結果，也就是 CountArr['length']。

否則繼續遞歸的減，讓 Num1 減去 Num2，并且 CountArr 多加一個元素代表又減了一次。

這樣就實現了除法：

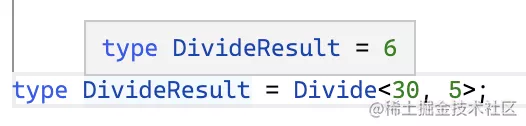
就這樣，我們通過遞歸的累減并記錄減了幾次實現了除法。

做完了加減乘除，我們再來做一些別的數值計算的類型體操。

數組長度實現計數

StrLen

數組長度可以取 length 來得到，但是字符串類型不能取 length，所以我們來實現一個求字符串長度的高級類型。

字符串長度不確定，明顯要用遞歸。每次取一個并計數，直到取完，就是字符串長度。

type StrLen<
    Str extends string,
    CountArr extends unknown[] = []
> = Str extends `${string}${infer Rest}` 
    ? StrLen<Rest, [...CountArr, unknown]> 
    : CountArr['length']

類型參數 Str 是待處理的字符串。類型參數 CountArr 是做計數的數組，默認值 [] 代表從 0 開始。

每次通過模式匹配提取去掉一個字符之后的剩余字符串，并且往計數數組里多放入一個元素。遞歸進行取字符和計數。

如果模式匹配不滿足，代表計數結束，返回計數數組的長度 CountArr['length']。

這樣就能求出字符串長度：

GreaterThan

能夠做計數了，那也就能做兩個數值的比較。

我們往一個數組類型中不斷放入元素取長度，如果先到了 A，那就是 B 大，否則是 A 大：

type GreaterThan<
    Num1 extends number,
    Num2 extends number,
    CountArr extends unknown[] = []
> = Num1 extends Num2 
    ? false
    : CountArr['length'] extends Num2
        ? true
        : CountArr['length'] extends Num1
            ? false
            : GreaterThan<Num1, Num2, [...CountArr, unknown]>;

類型參數 Num1 和 Num2 是待比較的兩個數。

類型參數 CountArr 是計數用的，會不斷累加，默認值是 [] 代表從 0 開始。

如果 Num1 extends Num2 成立，代表相等，直接返回 false。

否則判斷計數數組的長度，如果先到了 Num2，那么就是 Num1 大，返回 true。

反之，如果先到了 Num1，那么就是 Num2 大，返回 false。

如果都沒到就往計數數組 CountArr 中放入一個元素，繼續遞歸。

這樣就實現了數值比較。

當 3 和 4 比較時：

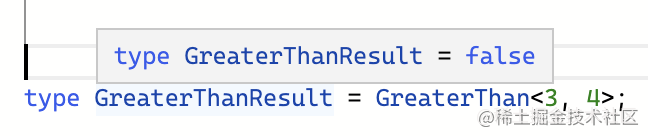
當 6 和 4 比較時：

Fibonacci談到了數值運算，就不得不提起經典的 Fibonacci 數列的計算。

Fibonacci

數列是 1、1、2、3、5、8、13、21、34、…… 這樣的數列，有當前的數是前兩個數的和的規律。

F(0) = 1，F(1) = 1, F(n) = F(n - 1) + F(n - 2)(n ≥ 2，n ∈ N*)

也就是遞歸的加法，在 TypeScript 類型編程里用構造數組來實現這種加法：

type FibonacciLoop<
    PrevArr extends unknown[], 
    CurrentArr extends unknown[], 
    IndexArr extends unknown[] = [], 
    Num extends number = 1
> = IndexArr['length'] extends Num
    ? CurrentArr['length']
    : FibonacciLoop<CurrentArr, [...PrevArr, ...CurrentArr], [...IndexArr, unknown], Num> 

type Fibonacci<Num extends number> = FibonacciLoop<[1], [], [], Num>;

類型參數 PrevArr 是代表之前的累加值的數組。類型參數 CurrentArr 時代表當前數值的數組。

類型參數 IndexArr 用于記錄 index，每次遞歸加一，默認值是 []，代表從 0 開始。

類型參數 Num 代表求數列的第幾個數。

判斷當前 index 也就是 IndexArr['length'] 是否到了 Num，到了就返回當前的數值 CurrentArr['length']。

否則求出當前 index 對應的數值，用之前的數加上當前的數 [...PrevArr, ... CurrentArr]。

然后繼續遞歸，index + 1，也就是 [...IndexArr, unknown]。

這就是遞歸計算 Fibinacci 數列的數的過程。

可以正確的算出第 8 個數是 21:

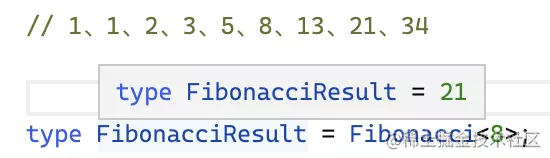
總結

TypeScript 類型系統沒有加減乘除運算符，所以我們通過數組類型的構造和提取，然后取長度的方式來實現數值運算。

我們通過構造和提取數組類型實現了加減乘除，也實現了各種計數邏輯。

用數組長度做計數這一點是 TypeScript 類型體操中最麻煩的一個點，也是最容易讓新手困惑的一個點。