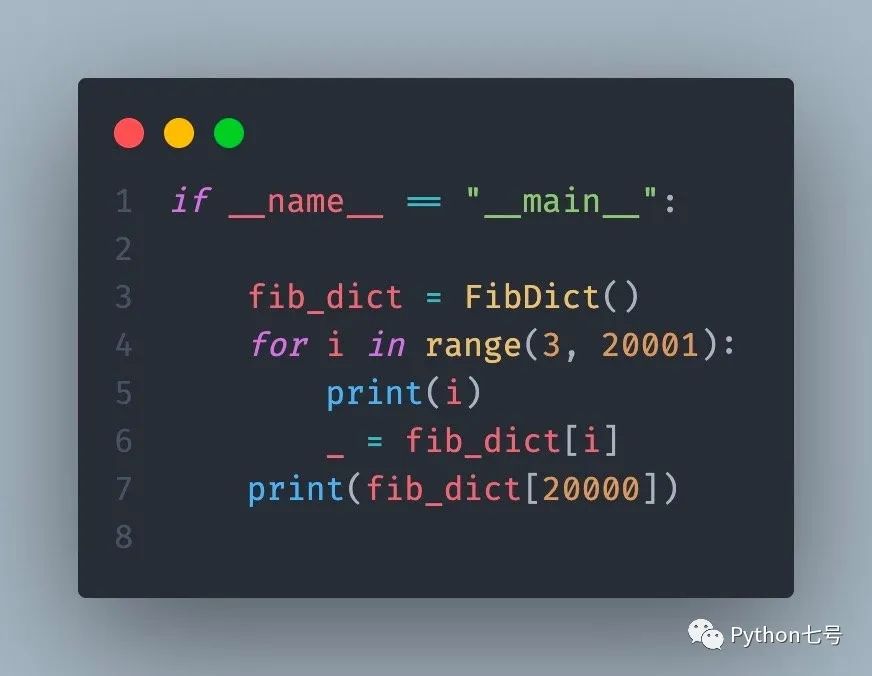
你知道瘋狂的字典嗎?
你好,我是 somenzz,Python 的靈活程度讓人發指,今天來分享一下關于字典的瘋狂操作,計算斐波那契數列,話不多說,先看代碼:
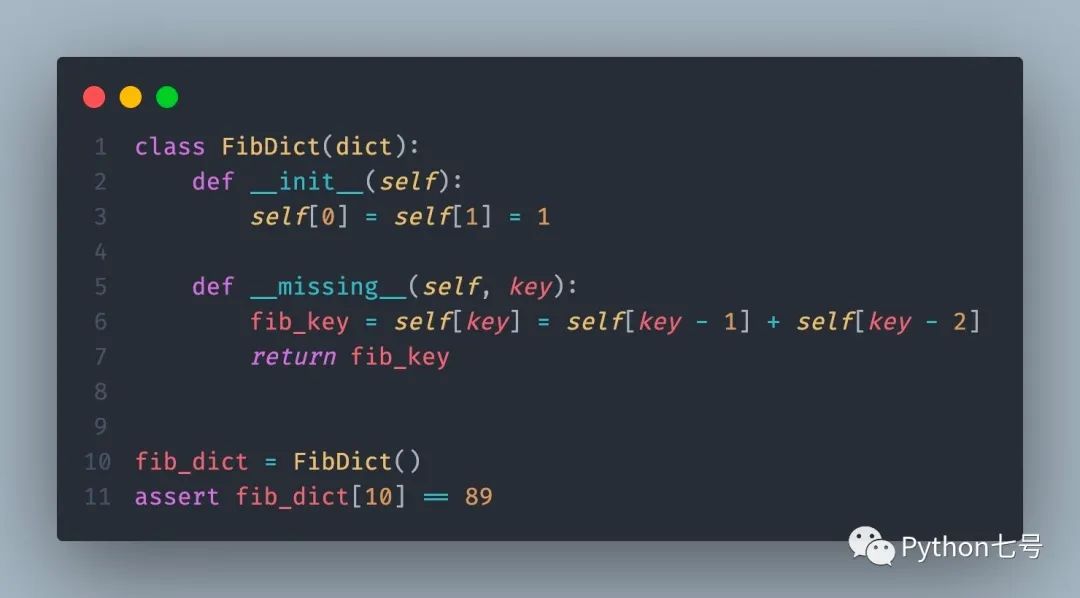
代碼定義了一個類 FibDict,繼承自 dict,自定義了魔術方法 __missing__ 當 dict 查找 key失敗(missing)的時候,會由 Python 解釋器自行調用改方法。換句話說,如果試圖從 dict 中獲取不存在的 key,就會執行這個方法。
因此計算 fib_dict[10] 就會執行這個方法,計算 fib_dict[9] 和 fib_dict[8],就這樣遞歸,一直到 fib_dict[0]和 fib_dict[1]。
這是遞歸,但是字典是一種 hash 表,只要計算過的數據不會重復計算,因此效率非常高。
我們可以驗證下計算 fib_dict[200] 的耗時:
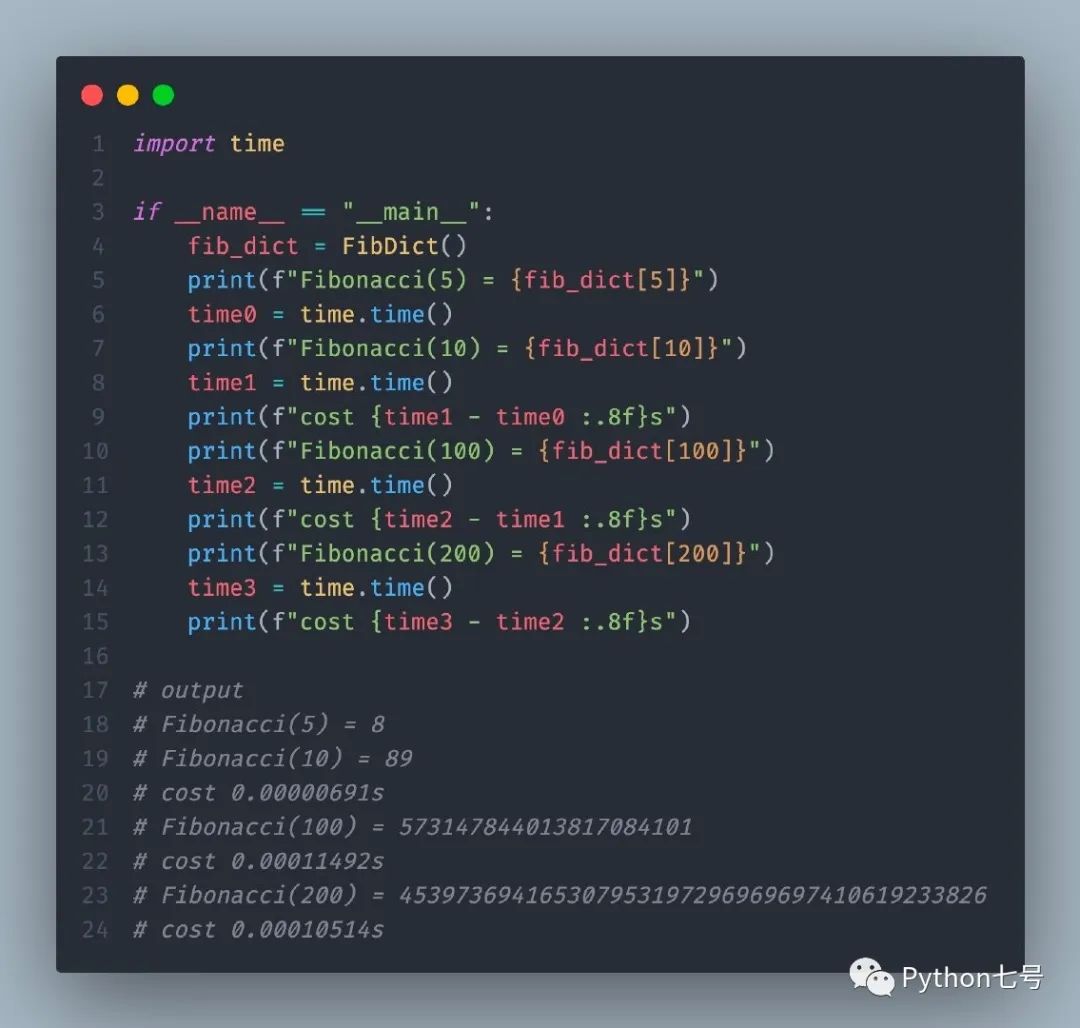
可以看出連 1 毫秒都不到。
不過,遞歸雖爽,可不要貪杯哦,任何事情都有極限,1000 是遞歸的默認極限(sys.getrecursionlimit() ==1000),如果你直接計算 fib_dict[501] 就拋出 RecursionError 異常。
你可能有個小小的疑問,為什么遞歸的深度是 1000,但我調用 501 次就不行了呢?其實原因在于 __missing__ 調用了 __setitem__,__setitem__ 又調用了 __missing__,因此每個缺失的 key 其實調用了兩次,所以超過 500 就會報錯。
但是,字典是有記憶的,如果你這樣調用它,永遠不會出現遞歸的問題: