一、什么是散列表

散列表是由數組擴展而來，其通過散列函數將元素的鍵值映射為下標，然后將元素存儲在數組中對應下標的位置。

關鍵字經過散列函數的計算得到一個散列值：hash(key)=hashCode；關于散列函數的選擇和設計，應該要滿足如下三個要求：

• 散列值一定是一個非負整數；
• 如果key1 == key2，那么hash(k1) == hash(k2)；
• 如果key1 != key2， 那么hash(k1) != hash(k2)；

這三個條件中，最難滿足的就是第三點，在現實中找一個這樣的散列函數幾乎是不可能的；比如著名的hash算法MD5、SHA、CRC等，都只是盡量均勻地散列，盡量避免散列沖突，但是做不到完全避免；而且由于數組空間有限，散列沖突就太正常不過了。

二、如何處理散列沖突

2.1 開放尋址法

線性探測

當散列沖突發生時，存儲位置已經被占用，那么就往后探測查找空閑位置；

如果想在散列表中查找某個元素，那么先計算得到散列值，找到該值對應的存儲空間，如果無值，說明要查找的元素不存在；如果有值，那么就比對值是否相等，相等則說明找到了，不相等那么就依次往后探測比較，要么找到，要么遇到空閑的存儲空間，說明查找的元素不存在；

如果想在散列表中刪除元素，那么不能將其簡單地刪除，因為刪除后會導致該空間后面的元素查找失敗，因為將需要刪除的元素置為邏輯刪除，如此才能不影響后面元素的查找過程；

線性探測方法弊端比較明顯，極端情況下插入、查找、刪除都需要探測n個元素才能找到目標位置，時間復雜度為O(n)；

二次探測

其實是在線性探測的基礎上每次探測增大步長，比如，每次探測當前次數的平方之后的位置，如此可以降低探測的次數的概率；但是不能解決線性探測同樣的弊端問題；

雙重散列

準備多個散列函數，如果第一個散列之后沖突了，就換一個散列函數，依次類推，直到找到空閑位置；但是一樣的，當元素增多后，所有散列函數都可能造成散列沖突；

使用場景

當數據量比較小，且裝載因子也比較小的時候，適合使用開放尋址法，比如ThreadLocalMap；

2.2 鏈表法

該種方法中，每個位置（可以稱為桶、槽）對應一個鏈表，所有散列值相同的元素都放在該位置對應的鏈表中，結構示意圖如下：

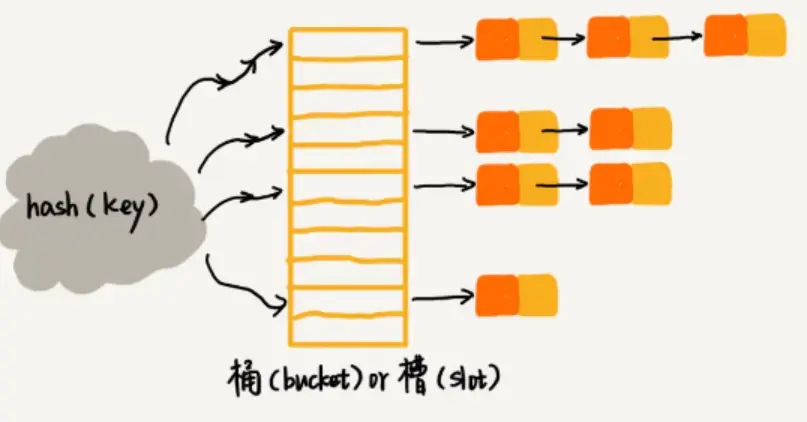
鏈表發解決散列沖突示意

當需要插入元素的時候，直接找到對應下標的插槽，插入鏈表即可，時間復雜度為O(1)；

當需要查找和刪除元素的時候，也是找到對應下標的插槽，然后遍歷鏈表查找即可，時間復雜度為O(n/m)，n是當前元素的個數，m是數組大小，假設散列是均勻的，那么時間復雜度就是鏈表的長度；

無論插入、查找還是刪除，時間復雜度都要優于開放尋址法；

適用場景：

當需要存儲的數據比較多，或者存儲的是大對象的時候，鏈表法比較合適，而且鏈表的長度過長時可以采用靈活的優化策略，比如紅黑樹來代替鏈表，如此查找時間復雜度最壞情況下的O(n)就能優化為O(logn)；

2.3 裝載因子

裝載因子=已經裝入散列表中的元素個數/散列表總的位置個數

裝載因子是用來衡量散列表當前盈滿程度的指標，其越大，說明散列沖突的概率就越高，當達到一定程度，就需要對散列表進行擴容了。

開放尋址法中，裝載因子不會超過100%，但是在拉鏈法中，裝載因子是會超過100%的；

三、散列函數的設計

散列函數不能太復雜，否則計算散列值就需要花費很多時間和資源；

散列函數生成的值要盡可能隨機并且均勻分布，最小化散列沖突，并避免某個槽中的鏈表過長；

裝載因子需要根據實際情況進行設置，當超過閾值會觸發散列表的擴容和rehash（重新申請一個大的散列表），時間復雜度將為O(n)；當小于某個閾值會觸發縮容和rehash；如果閾值設置地太大，就容易造成散列沖突，但如果設置地太小，就容易造成空間資源浪費；

為了避免擴容和rehash的影響，可以在裝載因子達到閾值時先申請大的散列表，但是不做rehash，當有新的元素需要插入的時候，就插入到新的散列表中，并從舊的散列表中取小量的元素進行rehash，當插入若干新元素后，舊的散列表中的所有元素就能逐漸rehash到新的散列表，如此是將整個rehash均攤到每次插入新元素操作中，用戶就不會感覺效率低了，此時的時間復雜度近似O(1)；

四、散列表HashMap分析

初始大小默認為16，如果事先能知道數據量，可以在初始化的時候就設置相應的大小，避免動態擴容。

最大裝載因子為0.75，觸發擴容時，會擴容為原來的兩倍。

當鏈表長度超過8時，鏈表就轉換為紅黑樹，從而提高增刪查改的效率；當紅黑樹元素個數小于8個的時候，就會再次轉換會鏈表，因為小數據量時紅黑樹為了維護平衡，性能并不比鏈表高。

散列函數并不復雜，足夠簡單高效，并且分布均勻。

int hash(Object key){
  // 鍵對象的
  hashcodeint h = key.hashCode();
  // capitity表示散列表的大小
  return (h ^ (h >>> 16)) & (capitity - 1);
}

五、散列表LinkedHashMap分析

也是通過散列表和鏈表組合在一起實現的，只不過此處的鏈表不是單鏈表，而是雙向鏈表，可以用來記錄元素插入的順序?