一、什么是堆

1.1 堆的定義

堆是一個完全二叉樹；

堆中的每一個節點的值都必須大于等于（大頂堆）or小于等于（小頂堆）其子樹中的每個節點的值；

1.2 堆上的操作

• 堆的存儲
• 我們在前面二叉樹的學習中就知道，完全二叉樹最理想的存儲方式便是數組，省去了左右節點的指針空間，而且不會造成很大的浪費。比如，節點位置為i，那么其左子樹就存放在2i的位置，右子樹就存放在2i+1的位置，其父節點在i/2的位置，向上向下索引都很快捷。
• 插入元素
• 我們一般都將待插入的數據作為一個節點放到當前堆的最后面，然后自下而上進行堆化操作。

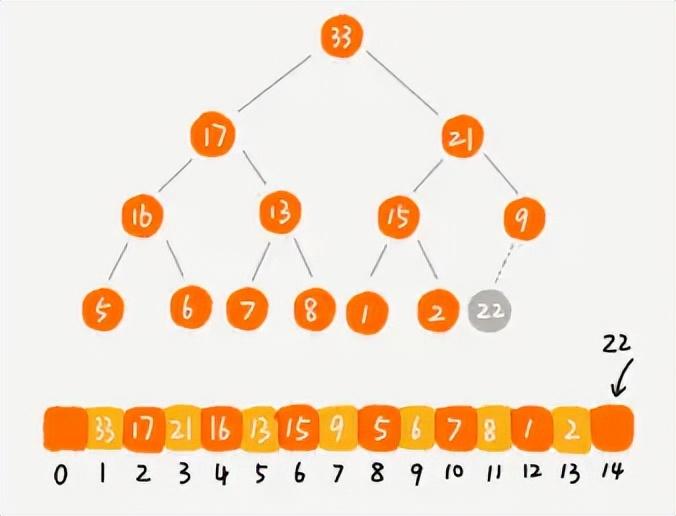
在堆的最后面插入一個節點

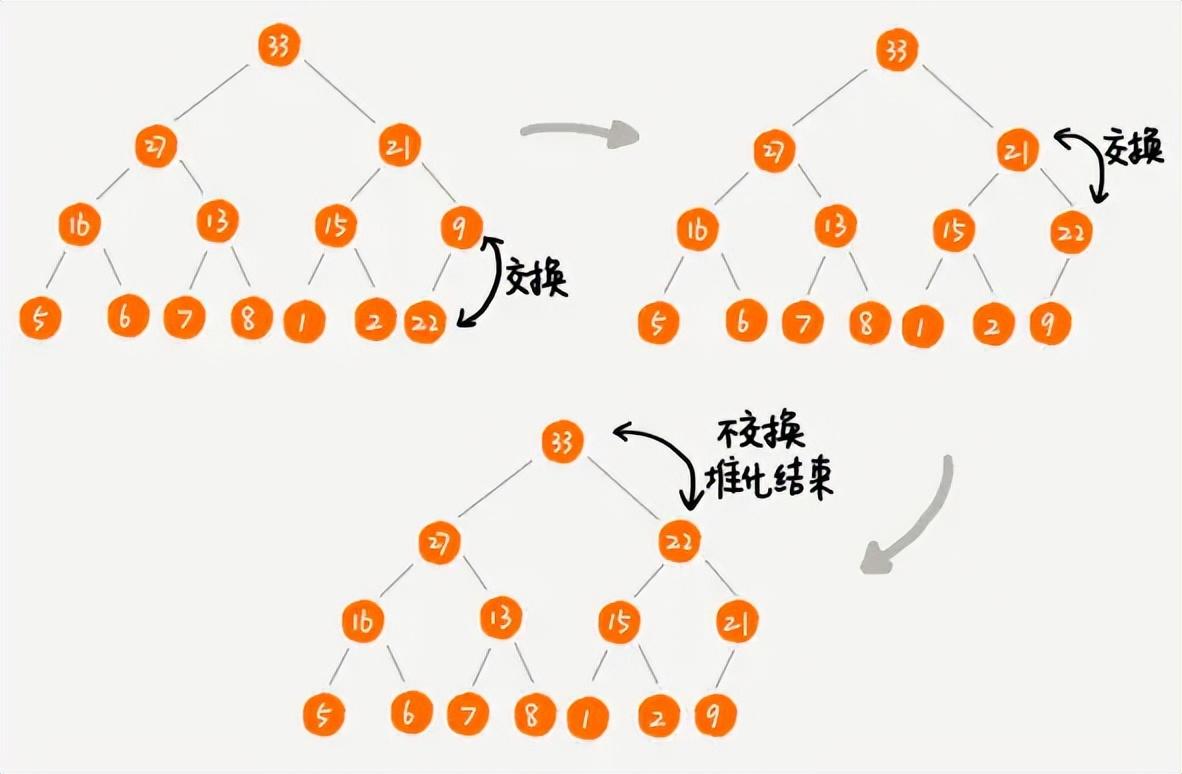
自下而上進行堆化

• 刪除堆頂元素
• 堆一般都是進行刪除堆頂元素，因為堆頂不是最大值就是最小值。一般不會刪除非堆頂元素，這是堆這種數據結構的特性決定的。
• 我們先將堆中的最后一個元素賦值給堆頂元素，然后再刪除最后一個元素，最后再進行自上而下的堆化操作。

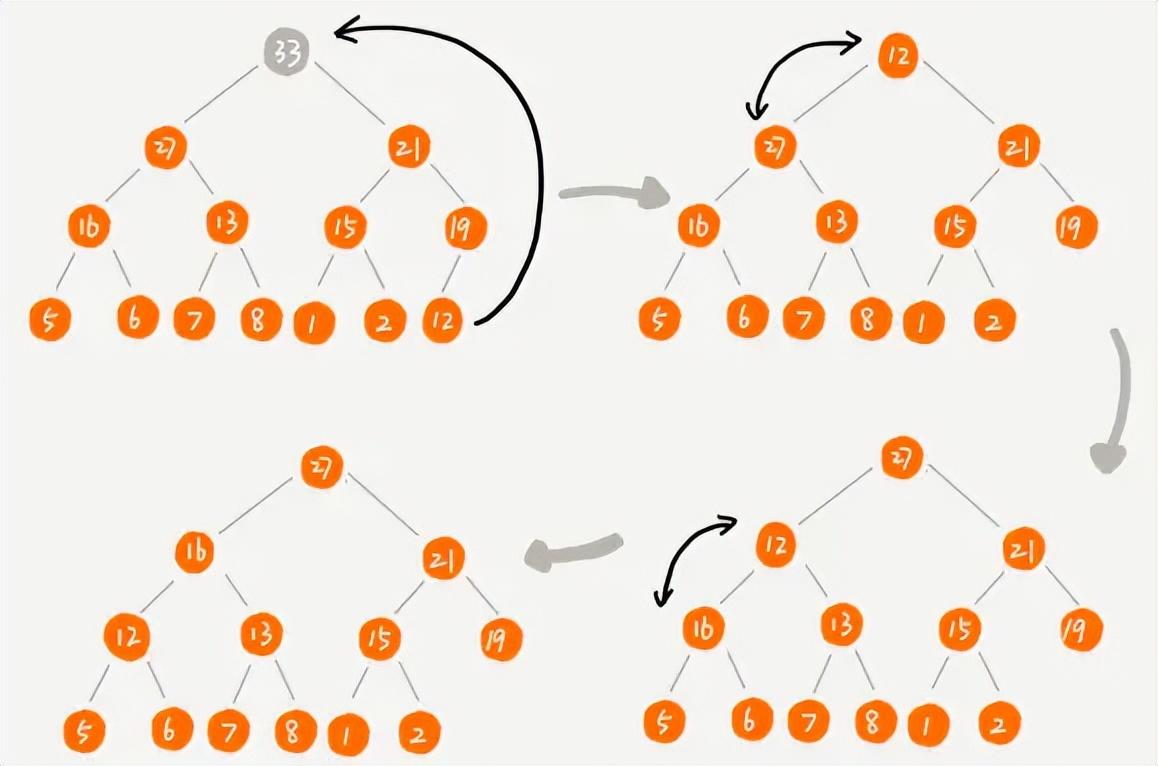
刪除堆頂元素的堆化操作

在如上插入和刪除堆頂元素的操作中，主要的時間消耗都在堆化這個過程中，堆化操作需要比較和交換的次數最大不會超過樹的高度，而前面我們說過，完全二叉樹的高度是2的對數，因此插入和刪除堆頂元素操作的時間復雜度是O(logn)。

二、 堆排序

給定一個數組，其中的元素都是無序雜亂的，我們怎么對它進行堆排序呢？

2.1 建堆

首先，我們需要將該數組建立為一個大頂堆（小頂堆），通常有以下兩種建堆的方法：

• 自上而下
• 把下標為1的元素作為原始堆，然后從下標2開始直到n，依次插入前面的堆中，就像前面講的插入元素操作一樣，不斷地進行堆化，然后形成一個大頂堆；其時間復雜度為O(nlogn)，不夠好。
• 自下而上
• 我們注意到，在完全二叉樹中，最后一個元素的下標除以2就能得到最后一個非葉子節點元素的下標n/2，光是葉子節點是無法進行堆化的，因此我們從n/2開始往前一直到下標為1為止不斷進行堆化，然后形成一個大頂堆；此過程就類似刪除堆頂元素之后的堆化過程；其時間復雜度為O(n)，優于第一種。

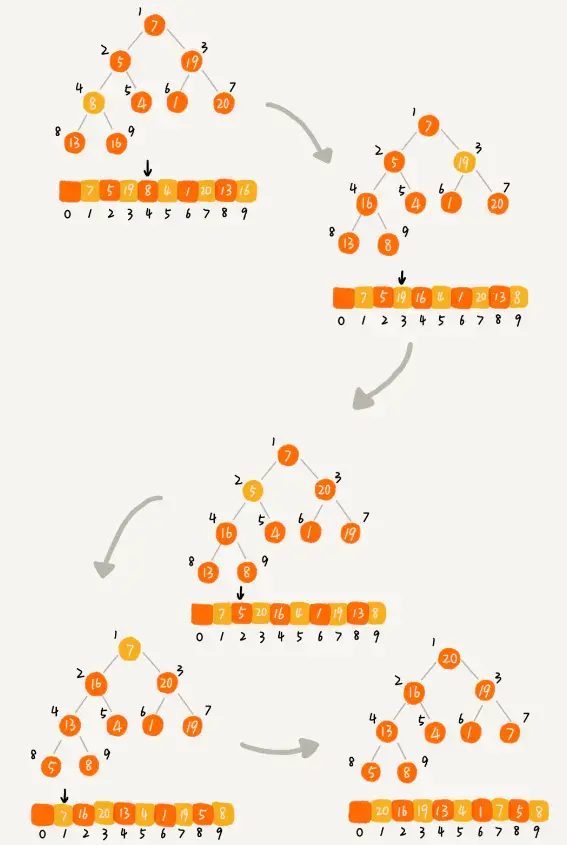
建堆時自下而上進行堆化的過程

2.2 排序

經過上一步的建堆操作，我們得到了一個大頂堆，但是數組中的數據看上去仍然是無序的，我們需要基于這個大頂堆把數組排下序。

首先從堆頂取出元素，這個元素肯定是最大的，把它和數組最后一個元素進行交換，放到位置n，然后堆中剩下的元素不斷地進行堆化，并始終取堆頂元素依次放到n-1,n-2,n-3的位置上，當堆中只剩最后一個元素的時候，此時數組就是一個有序數列了。

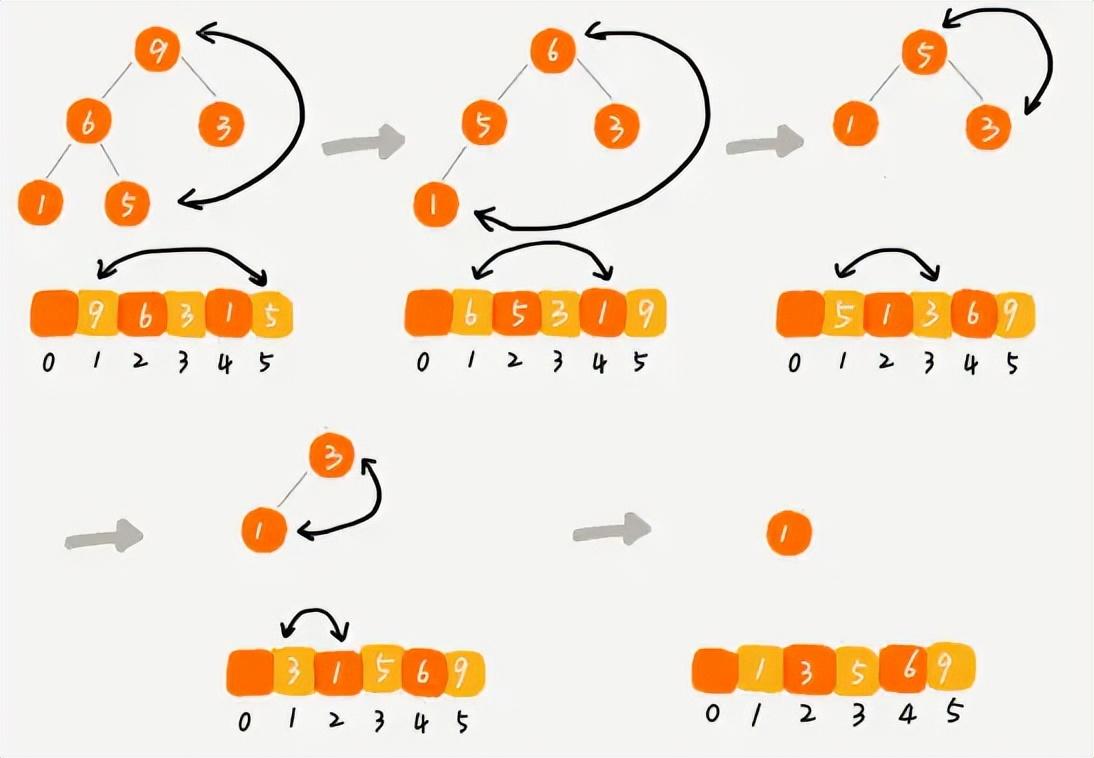
堆排序的過程示意

堆排序的過程中，我們需要對n個元素進行堆化操作，每次堆化操作時間復雜度取決于完全二叉樹的高度，所以最終得到堆排序的時間復雜度為O(nlogn)。

堆排序不需要借助很多的額外存儲空間，因此它屬于原地排序；

堆排序過程中會可能改變相同值的位置，所以不是穩定的排序算法；

2.3 堆排序和快速排序的比較

雖然堆排序和快速排序時間的時間復雜度都是O(nlogn)，但通常都認為堆排序的性能是比不上快速排序的。

• 堆排序的堆化過程中，在比較和交換元素時，讀取的數據并不是局部順序的；快速排序就是局部順序的；所以快速排序更加顯得CPU緩存友好，性能也會相對較好；
• 對于同樣的數列，堆排序數據的交換次數要多于快速排序；

三、堆排序的應用

3.1 堆排序

如上已經講解過了。

3.2 優先級隊列

優先級隊列中，數據的出隊不是按照入隊先后來決定的，而是按照優先級來的，優先級高（低）的就先出隊，實現優先級隊列的方法有很多，但是其中使用堆來實現是最為快捷高效的。比如Java中的PriorityQueue。

場景一：合并有序小文件

假設我們有n個小文件，每個大小為100MB，每個文件中存放的都是有序的字符串，我們如何把這n個小文件中的字符串有序地全都合并到一個大文件中呢？

這里有兩個方法：

• 按照歸并排序中的合并思路
• 設置n個指針各自指向每個文件的第一個字符串，將它們都加載到一個大小為n的數組中;
• 然后對數組進行遍歷尋找最小元素，時間復雜度為O(n)；并從數組中取出最小元素放到大文件中，將該元素從數組中刪除；
• 將該元素來源的小文件中的指針移向下一位取出元素放到數組中，然后重復第二步；
• 使用小頂堆
• 設置n個指針各自指向每個文件的第一個字符串，將它們都加載到一個小頂堆中，初始是一個建堆的過程；
• 取出堆頂元素放到大文件中，并將該元素從小頂堆的堆頂刪除，小頂堆會自動進行堆化；
• 將該元素來源的小文件中的指針移向下一位取出元素插入小頂堆中，小頂堆會自動進行堆化，然后重復第二步；
• 我們可以看到，這兩種方法的區別在于，前者需要每次遍歷數組找到最小值，后者則是有刪除和插入兩個堆化的過程。堆化過程的時間復雜度為O(logn)，明顯比遍歷數組的O(n)要好，所以方法二更加高效。

場景二：實現高性能定時器

假設我們使用定時器設置了很多個待執行的任務，那么如何實現定時觸發這些提前設定好的任務呢？

這里說三個方法：

• 程序每隔一段很小的時間（比如1秒）就進行任務掃描，找到最近要執行的任務進行執行，這種方法其實就是每1秒都要去尋找最小值，每次的時間復雜都是O(n)，而且，假設最近一個任務是定在2小時候執行的，那么這2小時內，掃描程序都是白執行的，浪費資源。這種方法并不推薦。
• 維護一個有序列表，比如使用快速排序，只要記住最小值的執行時間即可，等到了那個時間點程序再執行，如此掃描程序就不用一直去掃描了。
• 使用小頂堆來維護任務列表，記住堆頂任務的執行時間，等到了那個時間點程序再執行，如此掃描程序就不用一直去掃描了。
• 方法2和方法3其實是類似的，關鍵在于采取什么樣的數據結構和算法來獲取最小值。如果存在中途插入或者取消任務的情況，對于方法2來說，插入一個元素到有序列表中和從有序列表中刪除一個給定元素時間復雜度是多少呢？假設我們采用效率最高的二分查找，那么是O(logn)，但是插入和刪除元素是要搬移元素的，這個時間是O(n)，所以總的下來就是O(n)；如果使用方法3，那么無論插入還是刪除元素，都是一個堆化的過程，時間復雜度為O(logn)，所以方法3中使用堆更加高效。

3.3 求解Top-k問題

假設存量數據量為n，我們需要從n中找到Top-k的元素，并且針對不斷添加進來的數據，我們都要獲取最新的Top-k元素，這種問題應該怎么處理呢？

• 先從n中取出前k個元素，組成一個小頂堆，此時堆頂元素是最小的，我們從K+1個元素開始，和堆頂元素進行比較，如果比堆頂元素小，那么不做處理，繼續下一個；如果比堆頂元素大，那么把堆頂元素刪除，并插入k+1這個元素；等到n個元素全部遍歷完，那么小頂堆中的k個元素就是Top-k數據了；
• 對于外部不斷添加進來的數據其實思路是一樣的，把它當成數據源，不斷地和堆頂元素比較，重復上面的步驟操作即可。

時間主要耗費在一開始k個元素的初始建堆O(logk)上，還有刪除堆頂元素和插入新元素時的堆化O(logk)上；所以，總的時間復雜度應該為O(nlogk)，比使用排序來獲取Top-k的O(nlogn)還是要高效的。

3.4 求解中位數

對于一個無序的數列，怎么求出它的中位數呢？這要看數列是靜態的還是動態的。

如果是靜態的數列，那么我們先進行排序，比如快速排序O(nlogn)，然后如果總數是奇數，那么中位數就在n/2+1的位置上；如果總數是偶數，那么中位數有兩個，在n/2和n/2+1的位置上，隨便取一個即可。總的時間復雜度就是排序算法的時間復雜度O(nlogn)。

那如果是動態數列呢，我們需要維護數列的有序性，那么勢必要對新插入或者需要刪除的數據進行查找，時間復雜度為O(n)，還有數據搬移的O(n)，所以就會變得很低效，我們需要使用堆來解決這個問題。

我們先將已有數據排序，然后維護一個大頂堆和一個小頂堆，其中小頂堆存放最大的n/2個數據，堆頂元素是這n/2中最小的，大頂堆存放剩下的元素，堆頂元素是最大的。此時，中位數就是大頂堆的堆頂元素。

當動態數據添加進來時，我們將待添加元素和大頂堆的堆頂元素進行比較，如果小于等于，那么就插入大頂堆中；否則就和小頂堆的堆頂元素比較，如果大于等于，就插入小頂堆中。此時，如果小頂堆中的個數超過了n/2，就需要不斷地取出堆頂元素插入到大頂堆中，直至個數為n/2；如果小頂堆中的個數小于n/2，就需要不斷地取出大頂堆的堆頂元素插入到小頂堆中，直至小頂堆個數為n/2；

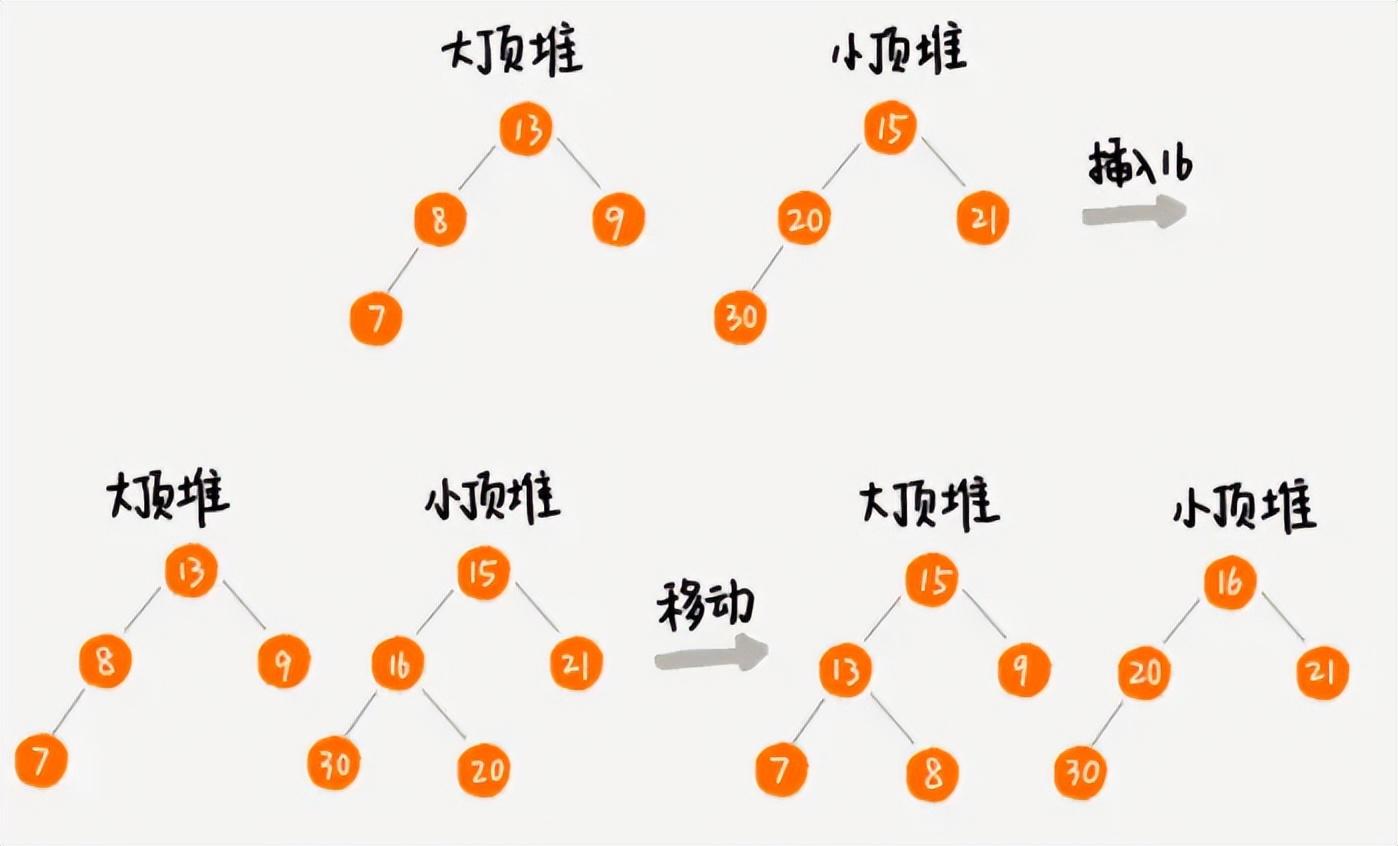
動態數列使用堆求解中位數過程示意

通過如上的過程，我們每次從大頂堆堆頂取出來的元素就是整個數列的中位數。整個過程的時間復雜度是多少呢？一開始初始化時的排序和建堆，由于數據比較少，可以算作常量；后續動態數據的插入或者刪除，就是一個堆化的過程，時間復雜度為O(logn)；大頂堆和小頂堆之間元素個數的調整不會有很多元素，所以也算作常數；因此，總的時間復雜度就是O(logn)。

既然動態數列求解中位數使用堆比較好，為什么靜態數列求解中位數不使用堆，而是排序呢？靜態數列也可以使用如上堆的方案進行求解中位數，但是時間復雜度也是O(nlogn)，和排序是一樣的，但是排序明顯更加地簡單，因此推薦使用排序的方案。

3.5 求解百分位數

求解中位數的問題其實就是求解百分位數問題的一種特殊情況， 中位數可以理解為百分位為50%，所以把中位數問題一般化的話，那么問題就是求解任意百分位數的問題。

思路和上述求解百分位是一樣的，比如我們要求解90%百分位的數，那么大頂堆中需要存放90%的數據，小頂堆中存放10%的數據，當動態地增加時需要依次和大頂堆、小頂堆的堆頂元素進行比較以決定插入到哪個堆中；如果插入或者刪除后，小頂堆中的數據占比不是10%了，就需要和大頂堆進行數據的交互以保證小頂堆數據的占比，如此才能保證大頂堆的堆頂元素就是我們需要的百分位數據。?