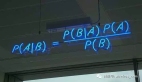對許多人來說,貝葉斯統(tǒng)計(jì)仍然有些陌生。因?yàn)樨惾~斯統(tǒng)計(jì)中會(huì)有一些主觀的先驗(yàn),在沒有測試數(shù)據(jù)的支持下了解他的理論還是有一些困難的。本文整理的是作者最近在普林斯頓的一個(gè)研討會(huì)上做的演講幻燈片,這樣可以闡明為什么貝葉斯方法不僅在邏輯上是合理的,而且使用起來也很簡單。這里將以三種不同的方式實(shí)現(xiàn)相同的推理問題。
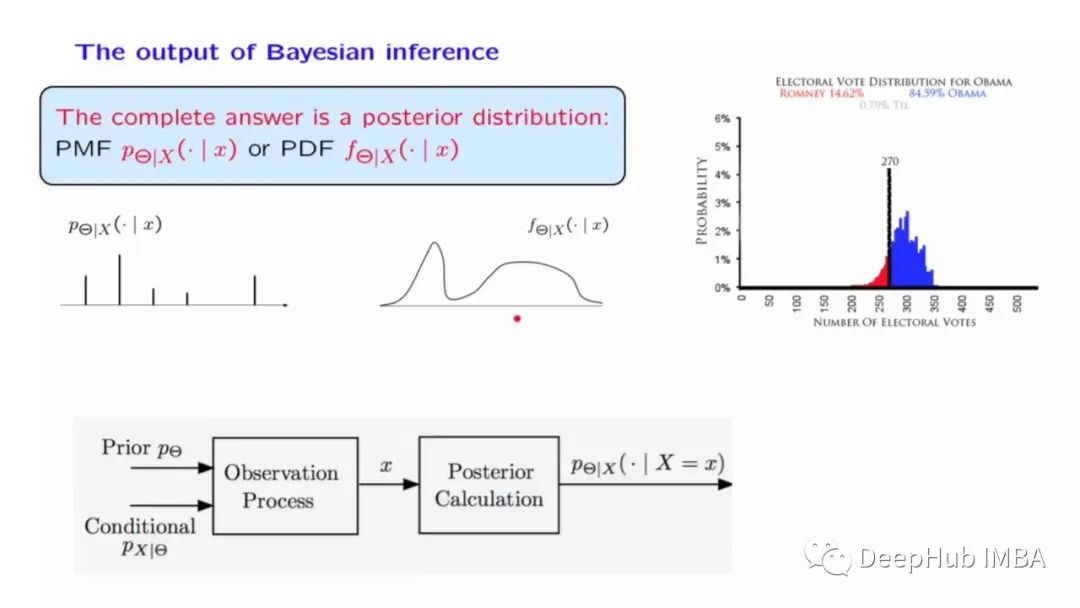
數(shù)據(jù)
我們的例子是在具有傾斜背景的噪聲數(shù)據(jù)中找到峰值的問題,這可能出現(xiàn)在粒子物理學(xué)和其他多分量事件過程中。
首先生成數(shù)據(jù):
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
import numpy as np
def signal(theta, x):
l, m, s, a, b = theta
peak = l * np.exp(-(m-x)**2 / (2*s**2))
background = a + b*x
return peak + background
def plot_results(x, y, y_err, samples=None, predictions=None):
fig = plt.figure()
ax = fig.gca()
ax.errorbar(x, y, yerr=y_err, fmt=".k", capsize=0, label="Data")
x0 = np.linspace(-0.2, 1.2, 100)
ax.plot(x0, signal(theta, x0), "r", label="Truth", zorder=0)
if samples is not None:
inds = np.random.randint(len(samples), size=50)
for i,ind in enumerate(inds):
theta_ = samples[ind]
if i==0:
label='Posterior'
else:
label=None
ax.plot(x0, signal(theta_, x0), "C0", alpha=0.1, zorder=-1, label=label)
elif predictions is not None:
for i, pred in enumerate(predictions):
if i==0:
label='Posterior'
else:
label=None
ax.plot(x0, pred, "C0", alpha=0.1, zorder=-1, label=label)
ax.legend(frameon=False)
ax.set_xlabel("x")
ax.set_ylabel("y")
fig.tight_layout()
plt.close();
return fig
# random x locations
N = 40
np.random.seed(0)
x = np.random.rand(N)
# evaluate the true model at the given x values
theta = [1, 0.5, 0.1, -0.1, 0.4]
y = signal(theta, x)
# add heteroscedastic Gaussian uncertainties only in y direction
y_err = np.random.uniform(0.05, 0.25, size=N)
y = y + np.random.normal(0, y_err)
# plot
plot_results(x, y, y_err)
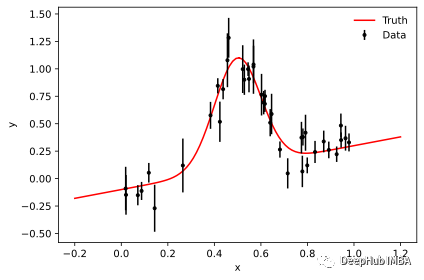
有了數(shù)據(jù)我們可以介紹三種方法了。
馬爾可夫鏈蒙特卡羅 Markov Chain Monte Carlo
emcee是用純python實(shí)現(xiàn)的,它只需要評估后驗(yàn)的對數(shù)作為參數(shù)θ的函數(shù)。這里使用對數(shù)很有用,因?yàn)樗怪笖?shù)分布族的分析評估更容易,并且因?yàn)樗玫靥幚硗ǔ3霈F(xiàn)的非常小的數(shù)字。
import emcee
def log_likelihood(theta, x, y, yerr):
y_model = signal(theta, x)
chi2 = (y - y_model)**2 / (yerr**2)
return np.sum(-chi2 / 2)
def log_prior(theta):
if all(theta > -2) and (theta[2] > 0) and all(theta < 2):
return 0
return -np.inf
def log_posterior(theta, x, y, yerr):
lp = log_prior(theta)
if np.isfinite(lp):
lp += log_likelihood(theta, x, y, yerr)
return lp
# create a small ball around the MLE the initialize each walker
nwalkers, ndim = 30, 5
theta_guess = [0.5, 0.6, 0.2, -0.2, 0.1]
pos = theta_guess + 1e-4 * np.random.randn(nwalkers, ndim)
# run emcee
sampler = emcee.EnsembleSampler(nwalkers, ndim, log_posterior, args=(x, y, y_err))
sampler.run_mcmc(pos, 10000, progress=True);
結(jié)果如下:
100%|██████████| 10000/10000 [00:05<00:00, 1856.57it/s]
我們應(yīng)該始終檢查生成的鏈,確定burn-in period,并且需要人肉觀察平穩(wěn)性:
fig, axes = plt.subplots(ndim, sharex=True)
mcmc_samples = sampler.get_chain()
labels = ["l", "m", "s", "a", "b"]
for i in range(ndim):
ax = axes[i]
ax.plot(mcmc_samples[:, :, i], "k", alpha=0.3, rasterized=True)
ax.set_xlim(0, 1000)
ax.set_ylabel(labels[i])
axes[-1].set_xlabel("step number");
現(xiàn)在我們需要細(xì)化鏈因?yàn)槲覀兊臉颖臼窍嚓P(guān)的。這里有一個(gè)方法來計(jì)算每個(gè)參數(shù)的自相關(guān),我們可以將所有的樣本結(jié)合起來:
tau = sampler.get_autocorr_time()
print("Autocorrelation time:", tau)
mcmc_samples = sampler.get_chain(discard=300, thin=np.int32(np.max(tau)/2), flat=True)
print("Remaining samples:", mcmc_samples.shape)
#結(jié)果
Autocorrelation time: [122.51626866 75.87228105 137.195509 54.63572513 79.0331587 ]
Remaining samples: (4260, 5)
emcee 的創(chuàng)建者 Dan Foreman-Mackey 還提供了這一有用的包c(diǎn)orner來可視化樣本:
import corner
corner.corner(mcmc_samples, labels=labels, truths=theta);
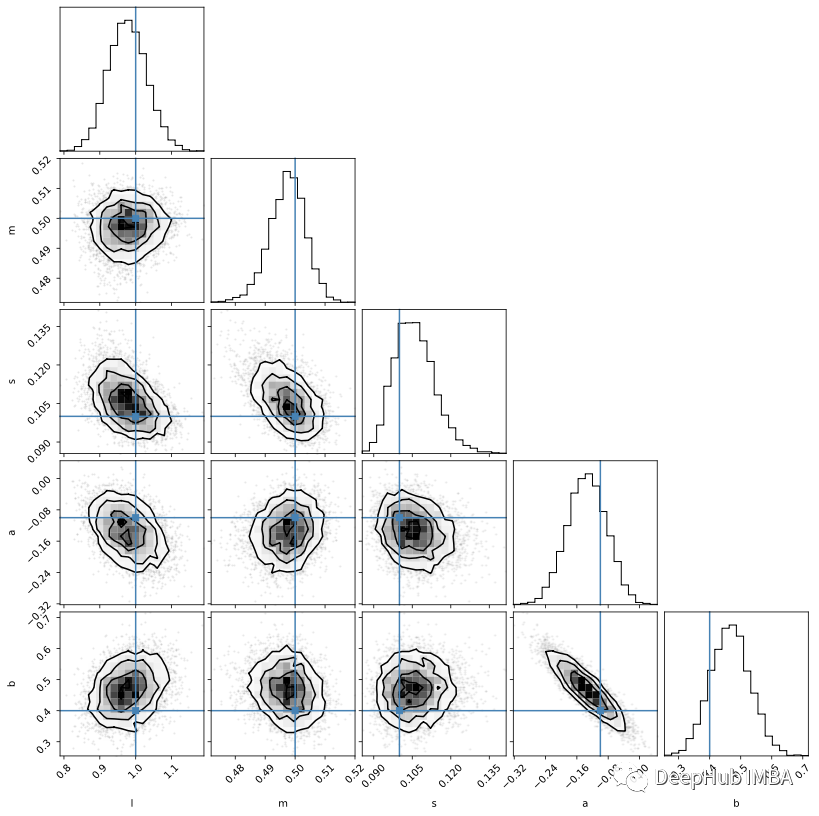
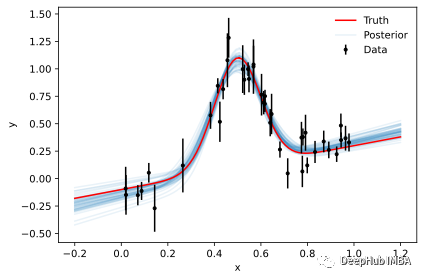
雖然后驗(yàn)樣本是推理的主要依據(jù),但參數(shù)輪廓本身卻很難解釋。但是使用樣本來生成新數(shù)據(jù)則要簡單得多,因?yàn)檫@個(gè)可視化我們對數(shù)據(jù)空間有更多的理解。以下是來自50個(gè)隨機(jī)樣本的模型評估:
plot_results(x, y, y_err, samples=mcmc_samples)
哈密爾頓蒙特卡洛 Hamiltonian Monte Carlo
梯度在高維設(shè)置中提供了更多指導(dǎo)。 為了實(shí)現(xiàn)一般推理,我們需要一個(gè)框架來計(jì)算任意概率模型的梯度。 這里關(guān)鍵的本部分是自動(dòng)微分,我們需要的是可以跟蹤參數(shù)的各種操作路徑的計(jì)算框架。 為了簡單起見,我們使用的框架是 jax。因?yàn)橐话闱闆r下在 numpy 中實(shí)現(xiàn)的函數(shù)都可以在 jax 中的進(jìn)行類比的替換,而jax可以自動(dòng)計(jì)算函數(shù)的梯度。
另外還需要計(jì)算概率分布梯度的能力。有幾種概率編程語言中可以實(shí)現(xiàn),這里我們選擇了 NumPyro。 讓我們看看如何進(jìn)行自動(dòng)推理:
import jax.numpy as jnp
import jax.random as random
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS
def model(x, y=None, y_err=0.1):
# define parameters (incl. prior ranges)
l = numpyro.sample('l', dist.Uniform(-2, 2))
m = numpyro.sample('m', dist.Uniform(-2, 2))
s = numpyro.sample('s', dist.Uniform(0, 2))
a = numpyro.sample('a', dist.Uniform(-2, 2))
b = numpyro.sample('b', dist.Uniform(-2, 2))
# implement the model
# needs jax numpy for differentiability here
peak = l * jnp.exp(-(m-x)**2 / (2*s**2))
background = a + b*x
y_model = peak + background
# notice that we clamp the outcome of this sampling to the observation y
numpyro.sample('obs', dist.Normal(y_model, y_err), obs=y)
# need to split the key for jax's random implementation
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
# run HMC with NUTS
kernel = NUTS(model, target_accept_prob=0.9)
mcmc = MCMC(kernel, num_warmup=1000, num_samples=3000)
mcmc.run(rng_key_, x=x, y=y, y_err=y_err)
mcmc.print_summary()
#結(jié)果如下:
sample: 100%|██████████| 4000/4000 [00:03<00:00, 1022.99it/s, 17 steps of size 2.08e-01. acc. prob=0.94]
mean std median 5.0% 95.0% n_eff r_hat
a -0.13 0.05 -0.13 -0.22 -0.05 1151.15 1.00
b 0.46 0.07 0.46 0.36 0.57 1237.44 1.00
l 0.98 0.05 0.98 0.89 1.06 1874.34 1.00
m 0.50 0.01 0.50 0.49 0.51 1546.56 1.01
s 0.11 0.01 0.11 0.09 0.12 1446.08 1.00
Number of divergences: 0
還是使用corner可視化Numpyro的mcmc結(jié)構(gòu):
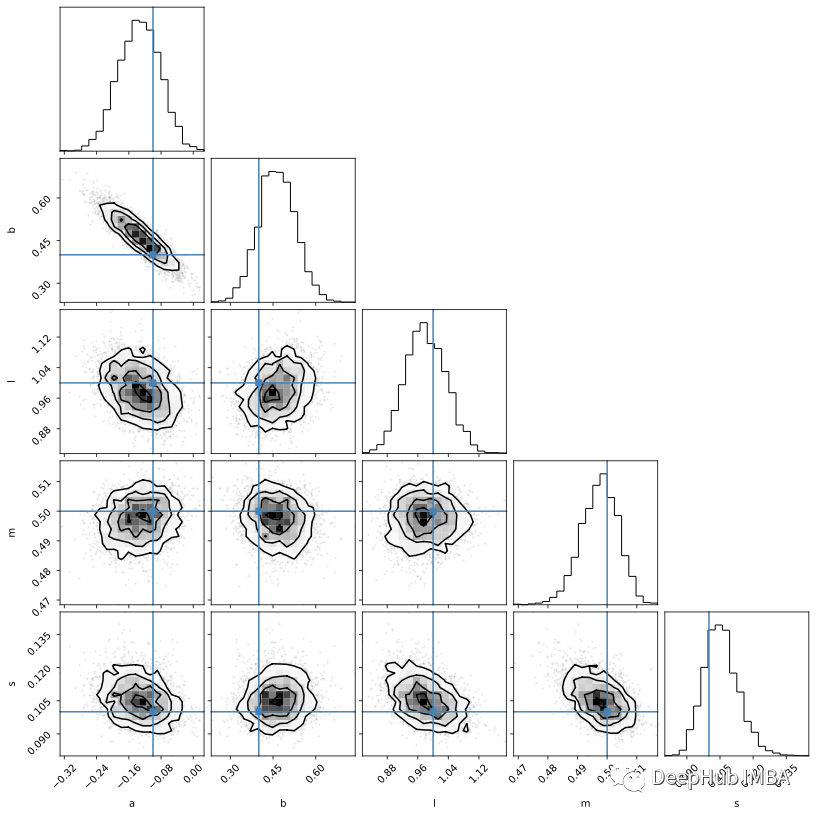
因?yàn)槲覀円呀?jīng)實(shí)現(xiàn)了整個(gè)概率模型(與emcee相反,我們只實(shí)現(xiàn)后驗(yàn)),所以可以直接從樣本中創(chuàng)建后驗(yàn)預(yù)測。下面,我們將噪聲設(shè)置為零,以得到純模型的無噪聲表示:
from numpyro.infer import Predictive
# make predictions from posterior
hmc_samples = mcmc.get_samples()
predictive = Predictive(model, hmc_samples)
# need to set noise to zero
# since the full model contains noise contribution
predictions = predictive(rng_key_, x=x0, y_err=0)['obs']
# select 50 predictions to show
inds = random.randint(rng_key_, (50,) , 0, mcmc.num_samples)
predictions = predictions[inds]
plot_results(x, y, y_err, predictions=predictions)
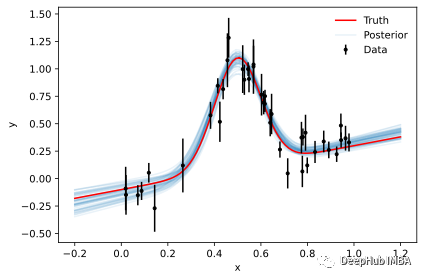
基于仿真的推理 Simulation-based Inference
在某些情況下,我們不能或不想計(jì)算可能性。 所以我們只能一個(gè)得到一個(gè)仿真器(即學(xué)習(xí)輸入之間的映射 θ 和仿真器的輸出 D),這個(gè)仿真器可以形成似然或后驗(yàn)的近似替代。 與產(chǎn)生無噪聲模型的傳統(tǒng)模擬案例的一個(gè)重要區(qū)別是,需要在模擬中添加噪聲并且噪聲模型應(yīng)盡可能與觀測噪聲匹配。 否則我們無法區(qū)分由于噪聲引起的數(shù)據(jù)變化和參數(shù)變化引起的數(shù)據(jù)變化。
import torch
from sbi import utils as utils
low = torch.zeros(ndim)
low[3] = -1
high = 1*torch.ones(ndim)
high[0] = 2
prior = utils.BoxUniform(low=low, high=high)
def simulator(theta, x, y_err):
# signal model
l, m, s, a, b = theta
peak = l * torch.exp(-(m-x)**2 / (2*s**2))
background = a + b*x
y_model = peak + background
# add noise consistent with observations
y = y_model + y_err * torch.randn(len(x))
return y
讓我們來看看噪聲仿真器的輸出:
plt.errorbar(x, this_simulator(torch.tensor(theta)), yerr=y_err, fmt=".r", capsize=0)
plt.errorbar(x, y, yerr=y_err, fmt=".k", capsize=0)
plt.plot(x0, signal(theta, x0), "k", label="truth")
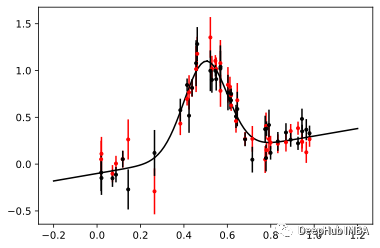
現(xiàn)在,我們使用 sbi 從這些模擬仿真中訓(xùn)練神經(jīng)后驗(yàn)估計(jì) (NPE)。
from sbi.inference.base import infer
this_simulator = lambda theta: simulator(theta, torch.tensor(x), torch.tensor(y_err))
posterior = infer(this_simulator, prior, method='SNPE', num_simulations=10000)
NPE使用條件歸一化流來學(xué)習(xí)如何在給定一些數(shù)據(jù)的情況下生成后驗(yàn)分布:
Running 10000 simulations.: 0%| | 0/10000 [00:00<?, ?it/s]
Neural network successfully converged after 172 epochs.
在推理時(shí),以實(shí)際數(shù)據(jù) y 為條件簡單地評估這個(gè)神經(jīng)后驗(yàn):
sbi_samples = posterior.sample((10000,), x=torch.tensor(y))
sbi_samples = sbi_samples.detach().numpy()
可以看到速度非常快幾乎不需要什么時(shí)間。
Drawing 10000 posterior samples: 0%| | 0/10000 [00:00<?, ?it/s]
然后我們再次可視化后驗(yàn)樣本:
corner.corner(sbi_samples, labels=labels, truths=theta);
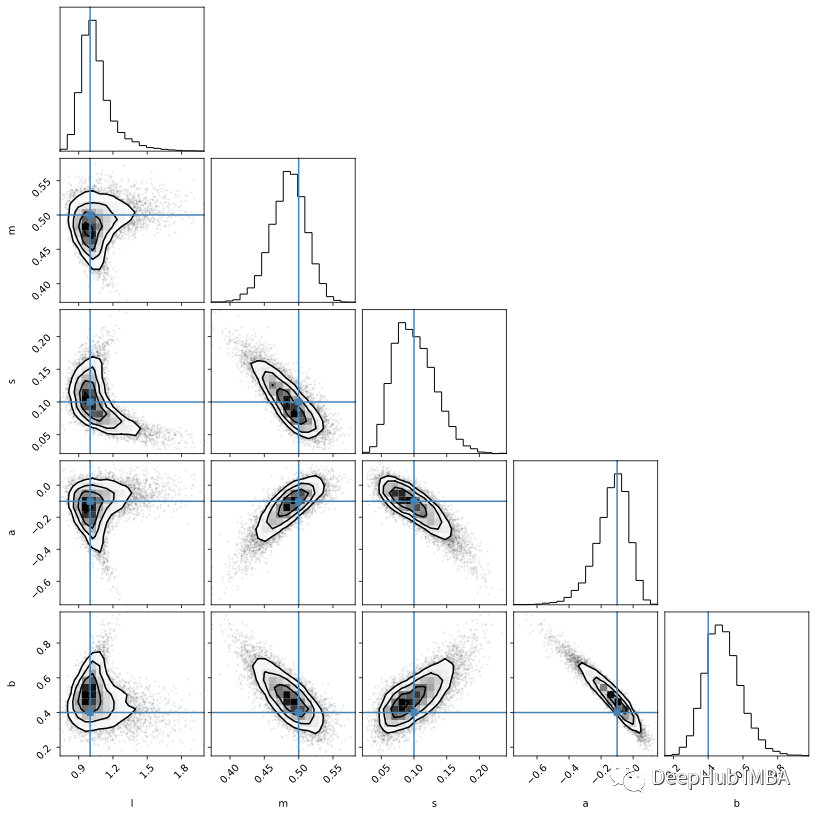
plot_results(x, y, y_err, samples=sbi_samples)
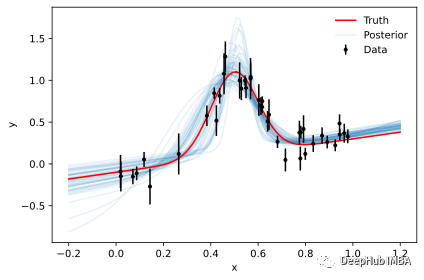
可以看到仿真SBI的的結(jié)果不如 MCMC 和 HMC 的結(jié)果。 但是它們可以通過對更多模擬進(jìn)行訓(xùn)練以及通過調(diào)整網(wǎng)絡(luò)的架構(gòu)來改進(jìn)(雖然并不確定改完后就會(huì)有提高)。
但是我們可以看到即使在沒有擬然性的情況下,SBI 也可以進(jìn)行近似貝葉斯推理。