1、背景

本文主要介紹使用卡諾圖化簡多變量邏輯表達式的原理與方法，此方法是一種邏輯計算思想，在任意技術平臺類似的多元化場景中均可適用。

本文以客戶端的一個業務場景為例，從舉例分析到實際應用的步驟，介紹卡諾圖工具的使用，讓我們輕松應對復雜交互或多條件判斷的編碼。

2、使用場景舉例

開發中我們有時會遇到一些復雜條件的交互要求，它們共同操作公共控件，使得交互邏輯在流程中變得極為復雜，如何簡便高效地處理和維護這些判斷邏輯，是我們可以思考的方向。

先來看一個這樣的業務場景，為方便說明已稍作簡化。在一個拍攝頁面中有如下幾個控件：添加音樂按鍵，濾鏡按鍵，拍攝鍵，特效選擇器，特效清除鍵?（圖1.1 所示紅圈處），它們在拍照就緒狀態下是都顯示的，然后用戶可能的操作流程有2種：拍照片和拍視頻，而這2種操作可以分別有3個不同的效果選擇：增加音樂，增加濾鏡，增加特效，則此例中共有 2 * 3 = 6? 種不同操作方式的組合，這些操作又分別涉及不同的控件，需要它們配合完成相應操作。即 m 種操作和 n 種效果，共 m*n 種組合方法。

而聰明的你則要處理它們全部的交互邏輯。此頁面更多詳細的交互要求可參考發布工具[拍攝頁] 交互要求 [1]。

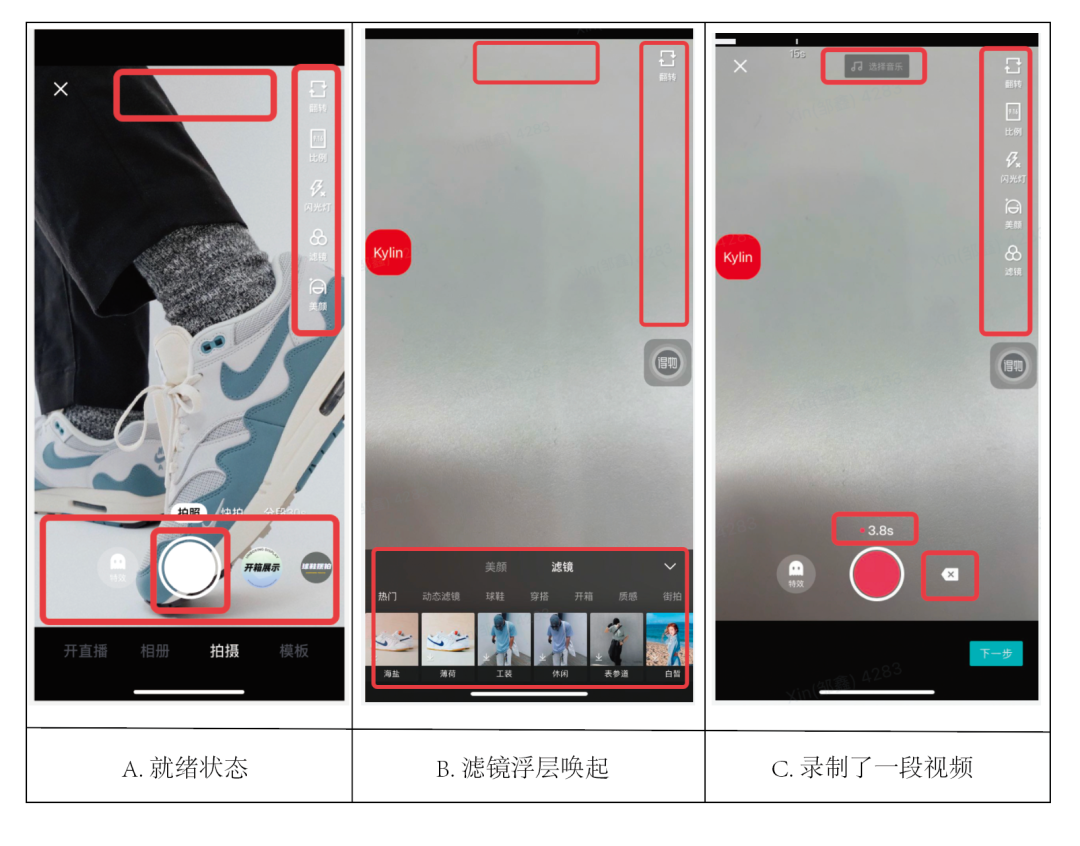
圖 1.1  拍攝頁的不同狀態UI與交互效果示意

主要交互要求是什么呢？參考看著上圖，我們隨便舉幾個粟子好了，比如：

?? 已拍了照片或視頻不能顯示音樂鍵

?? 濾鏡浮層打開后要隱藏音樂鍵、拍攝鍵和特效選擇器

?? 關閉浮層后要把這些控件重新顯示出來

?? 有特效時要顯示清除鍵

還有其他更多細節限于篇幅就不羅列了。多樣化的操作帶來邏輯的復雜變化，比如視頻拍了一半，暫停來切換特效，而特效控件在有視頻和無視頻時展示的控件又不同，或刪掉視頻去選濾鏡、選音樂等等，是不是已經暈了？這里面還有些其他可能想都想不到的細節出現，由此足以看出交互要求的復雜性了。如圖1.1 所示，紅圈處為頁面在不同狀態下發生的主要變化。

使用響應式編程或許可以解決部分問題，但由于每個控件狀態并不是由單一參數決定的，所以我們仍需要在它們各自的監聽方法里寫全部相關參數的判斷邏輯，這模式對解決此場景的根本問題似乎并無太多幫助。主要問題出在哪兒呢？

2.1 痛點

一句話總結問題：不同的交互方法之間產生了冗余的先后依賴而阻礙了業務的狀態轉移，使邏輯不夠清晰，代碼難以維護。

怎么辦呢？你可能會說，我們可以按操作的內容來分類，把控件按操作類別分裝入不同的父容器中，然后在相應操作方法里控制這容器即可。

嗯想法很不錯，但實際這么做了然后我們會發現，例如說在上述場景里，在關閉浮層時，若已經拍了一段視頻，則還需要單獨判斷音樂鍵的顯示狀態，或是此時還沒選擇特效，就不能把清除鍵也顯示出來。

于是我們開始意識到，這個場景下的業務方法不能完全獨立出來使用。抽象來說，這些操作之間相互有順序的依賴，它們不能嚴格滿足邏輯表達式加法交換律，即某些情況 A操作 和 B操作 的順序不同會導致結果不同：

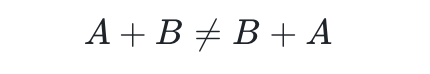
還有許多類似的corner case，我們若把全部case分列出來，則它們的控制邏輯會像星辰一樣散落在各個處理方法中，作為中介作用的容器也會層層疊疊地出現，然后我們還需要寫一大坨處理各種子狀態、容器控件的方法，再根據當前用戶操作去相應地調用；當頁面里的控件數量增多，或需求變化了，或控件要增多/減少時，整個流程就不再具有清晰的層級關系或先后邏輯了。

更麻煩的是，我們每次看似簡單的增刪改操作，都要把相應業務的上下游方法全部梳理一遍，甚至和其他功能有交互的地方，也要關注到，這樣的邏輯產生過高的復雜度也容易產生疏漏。要維護好這么一堆面條代碼將不是一件令人愉快的事；若是對業務不熟悉就做修改，極易踩坑，導致改了A處又壞了B處，修了B處又影響了C處，正是因為各子業務的方法存在過度耦合，出bug就沒完沒了。

那么我們還有更優雅的方式來處理這種場景么？

2.2 邏輯狀態抽象

不如我們先換個角度來看。

通過觀察梳理業務要求[1]可發現，其實我們并不需要知道用戶之前做過什么操作，因為控件的交互只與個別參數相關，即交互是依賴于某個變量而非業務流程。我們若將這些參數用bool值來確定，就可以唯一決定當前的頁面狀態，并且這些狀態在一個交互中是相互獨立的，即當前狀態與它之前的狀態無關。

也就是說：與其說當前操作需要什么交互，不如說當前操作發生時，相關參數處于什么狀態，再由這些狀態即可決定頁面所需的交互。

例如，當濾鏡浮層dismiss時，哪些控件需要重新顯示出來呢？那得看此時是否已有錄視頻，是否已有特效，是否已有音樂等等，這些參數綜合起來，就唯一決定了當前的狀態，就可計算出所需邏輯。

很棒，我們走到這里問題已解決一大半了。即引出本文主題：卡諾圖。

2.3 狀態化簡工具：卡諾圖

若是滿足上述這些條件，那么我們就可以使用邏輯表達式來方便地描述它們，而邏輯式的化簡就可以用卡諾圖方便地完成。

至此，我們就將問題由具體業務流程轉化為：如何使用關聯的變量建立邏輯式描述頁面的狀態。這樣一來就把狀態從流程中剝離出來了，你會發現，從這個角度看問題，無論流程怎么變，所做操作最終都會落入某個狀態，這才是我們要找的關鍵聯系：

相關變量 --(確定)--> 邏輯表達式 --(確定)--> 控件狀態

這個過程，也是我們計算狀態轉移的方法，只用上面3步，掌握之后再遇到類似場景，我們完全可以無腦按套路來處理邏輯狀態就ok了，讓代碼清爽簡潔，敏感肌也能用。

2.4 舉例使用

卡諾圖具體怎么用呢？

我們還是繼續看上面的例子，就寫一個方法 ：func refreshCurrentStatusUI()，用于在任意時刻需要刷新頁面狀態時獲得所需狀態，而不用關心具體當前的操作或流程是什么，以便把狀態從業務流程中獨立出來。

方法結構也是最基本的思路，方法有格式如下：

func refreshCurrentStatusUI()    // 獲取當前變量狀態    let A: Bool = isA()    let B: Bool = isB()    let C: Bool = isC()    let D: Bool = isD()    ...    // 設置控件交互    view01.isHidden = ABCD表達式1    view02.isHidden = ABCD表達式2    view03.isHidden = ABCD表達式3    ...}

在實際應用的方法體里，把與業務場景相關的參數狀態列出來，比方說，獲取與羅列的控件相關的幾個必需變量，為了表述方便，這里用符號ABC來代表參數，當然你也可以用其他的符號。

各參數說明如下：

A：是否有視頻

B：是否有特效

C：是否有子特效

D：是否已拍照填充了子特效

F：是否有音樂

按上述方式填充方法體，有幾個參數你就列出幾個，簡單又直觀：

func refreshCurrentStatusUI()    // 當前數據狀態    let hasVideo: Bool = isProgressHasSections()           // A: 是否已錄制視頻    let hasEffect: Bool = hasSpecialEffect()               // B: 是否已選有特效    let hasSubEffect: Bool = hasSubStickers()              // C: 是否帶有子特效    let hasSubEffectPhoto: Bool = hasSubStickersGetPhoto() // D: 是否已拍照填充了子特效 subEffect    let hasMusic: Bool = currentMusicData != nil || musicID > 0 // F: 是否有音樂...}

有一點細節需要注意的是：上述變量用到的值一定要在方法體里即用即取，不建議從方法外傳值進來，因為多線程和并發的存在，則有的屬性變量值可能在本方法開始調用后被其他線程或方法修改，即狀態已發生了改變，而傳入的值狀態就已經滯后，導致本方法計算出的控件狀態不是預期最新的狀態了。

然后我們只需要繼續在這個方法里，使用上述變量當下的值，計算每個控件狀態的邏輯表達式，根據結果來刷新各控件狀態即可：

// 拍攝鍵takeButton.isHidden          = !(hasVideo || hasSubEffectPhoto)
// [刪除視頻片段]按鍵deleteButton.isHidden        = !(hasVideo || hasSubEffectPhoto)
// 特效選擇器specialEffectPicker.isHidden = hasVideo || hasSubEffectPhoto
// 特效浮層鍵stickerSelectionButton.isHidden    = !hasVideo && (hasEffect || hasSubEffect) || hasSubEffectPhoto // (!A)(B+C)+D
// 特效清除鍵specialEffectClearButton.isHidden  = !hasEffect || (hasSubEffect || hasSubEffectPhoto) // !B || (C || D)

這樣一來，即使后面需要增加更多控件，或增加邏輯參數，都可以在這個方法里統一處理，然后在需要刷新頁面的地方調用，而我們不需要關心具體操作發生時頁面的上一個狀態。到這里，業務方法就大功告成了，我們保證了在任意操作流程中交互的狀態都是可唯一確定的。

OK 下一步，邏輯表達式要怎么做呢？

3、卡諾圖簡介

卡諾圖[2]可以用于表示和化簡邏輯函數。

一個邏輯函數的卡諾圖，就是將此函數的最小項表達式中的各最小項填入相應的特定方格圖內，這樣的方格圖就是卡諾圖。

舉例，比如 4變量的卡諾圖，記ABCD?為所用4個變量，行與列頭為4個變量分別對應的取值（true 或 false，對應記為邏輯 1 或 0 方便計算），16個方格中相鄰的數字0~15依順序代表方格邏輯相鄰：

圖3.1  卡諾圖邏輯相鄰格式

3.1 代數含義

一個邏輯函數，如果有 n 個變量，則有$$2^n$$個最小項，最小項為所有所有變量的積，也就是所有變量的與門邏輯。

3.2 特點

• 邏輯函數有幾個變量，就有幾個因子
• 每個變量都是它的一個因子
• 每一變量或以原變量形式出現(A、B、C)?,或以非變量形式出現(!A、!B、!C)
• 每個乘積的組合僅出現一次，且取值為1
• 任何邏輯函數都可以轉換成最小項的形式

3.3 相鄰組合

任何一對相鄰最小項可以組合為比原最小項本身少一個變量的單項。

3.4 邏輯相鄰

• 最上面的一列和最下面的一列邏輯相鄰，可以相互化簡
• 最左邊一列和最右邊的一列邏輯相鄰，可以相互化簡
• 四個角邏輯相鄰，可以相互化簡
• 要更好地理解上述規則和邏輯相鄰，我們需要使用格雷碼。

4、格雷碼編碼規則

4.1 格雷碼原理

畫卡諾圖的時候需要先將所有變量可能以格雷碼的形式排列在方格兩側，所有變量有$$2^n$$個，格雷碼的基本特點就是任意兩個相鄰的代碼只有一位二進制數不同，主要用于在數字電路中變化時每次就只有一位發生變化，用以提高電路的穩定性[3]。

表3.1  格雷碼編碼規則

4.2 格雷碼規則

自然二進制數到格雷碼：保留二進制碼的最高位作為格雷碼的最高位，而次高位格雷碼為二進制碼的高位與次高位相異或，而格雷碼其余各位與次高位的求法相類似。

格雷碼到自然二進制數：保留格雷碼的最高位作為自然二進制碼的最高位，而次高位自然二進制碼為高位自然二進制碼與次高位格雷碼做相異或計算，而自然二進制碼的其余各位與次高位自然二進制碼的求法相類似。

以一個四位二進制數來舉例，二進制（abcd）,依據規則轉換為格雷碼就是

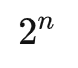
即異或計算【a, (a^b), (b^c), (c^d)】， 依據規則繼續轉化二進制的話就是 【a, (a^a^b), (a^a^b^b^c), (a^a^b^b^c^c^d)】，化簡之后仍然可以得到（abcd）。

5、卡諾圖簡單邏輯化簡

5.1 化簡方法

邏輯化簡的實際目標是盡可能地減少表達式中包含的項數以及各項包含的變量數[4]。下圖為三變量卡諾圖結構，m0~m7表示變量ABC的8種狀態[7]。

圖5.1  三變量卡諾圖

此圖即為基本卡諾圖的形式，兩側變量依據格雷碼形式，目的就是畫卡諾圈時要將里面的 1 全都包括在內[5]。

類似的，有4變量卡諾圖描述16種狀態，其結構如下所示：

圖5.2  四變量卡諾圖

卡諾圖填寫完成后，就可以作卡諾圈了，通過圈選與合并狀態，我們可以將邏輯多項式化簡得到其最小項表達式。

5.2 卡諾圈原則

卡諾圈原則：所作卡諾圈盡量大，卡諾圈的數量盡量少

• 卡諾圖上處在相鄰、相對、相重位置的小方格所代表的最小項為相鄰最小項。
• 兩個小方格相鄰, 或處于某行(列)兩端時，所代表的最小項可以合并，合并后可消去一個變量。
• 四個小方格組成一個大方格、或組成一行（列）、或處于相鄰兩行（列）的兩端、或處于四角時，所的表的最小項可以合并，合并后可消去兩個變量。
• 八個小方格組成一個大方格、或組成相鄰的兩行（列）、或處于兩個邊行（列）時，所代表的最小項可以合并，合并后可消去三個變量。
• 對于方格中帶有未知變量x的，是可圈可不圈的，依據自己實際情況而定[6]。

5.3 化簡舉例與步驟

用上面拍攝頁的例子，我們怎么用那幾個變量，得到最終的交互結果呢？一起按步驟一步步來看。

5.3.1 抽出變量

各變量已有對應的取值方法，為方便使用變量，我們計算中用ABC符號來代表各參數，比如 A 代表是否已錄視頻，取0為false，1為true；其他變量同理，可寫出：

let hasVideo          // A: 是否已錄制視頻let hasEffect:        // B: 是否已選有特效let hasSubEffect:     // C: 是否帶有子特效let hasSubEffectPhoto // D: 是否已拍照填充了子特效 subEffectlet hasMusic          // F: 是否有音樂

然后拿出需要計算的控件，先用一個邏輯比較簡單的，比如拍攝鍵 takeButton? ，然后把與之相關的變量找出來，按照業務要求得知，它的顯示與隱藏只和“是否有視頻”、“是否填充子特效”這兩個參數有關，當然你也可以把看似相關的其他參數帶進去，在化簡完成后，無關參數最終會被消去。

5.3.2 填充卡諾圖

那么，與拍攝鍵相關的變量就是 hasVideo，hasSubEffectPhoto? ，對應符號是 A，D ，分別取0和1值。在下圖中，A為行，B為列，填充到2變量的卡諾圖中：

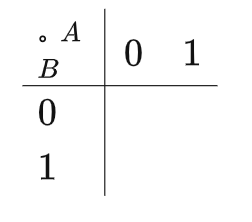
圖5.3  初始化卡諾圖

其中行代表A的取值，列為B的取值情況，它們相交處共同描述了AB全部4種取值：00，01，10，11。

然后，對應每一種取值情況，我們需要思考 拍攝鍵 takeButton? 的顯示狀態，并在相應空格里填入0或1，含義由我們來定，這里取0為隱藏，1為顯示較直觀，那么有：

A = 0，B = 0 ?-->無視頻 & 無填充子特效時，拍攝鍵要隱藏，所以取0，則在坐標(0,0)處填0；

A = 0，B = 1 ?-->無視頻 & 有填充子特效時，拍攝鍵要顯示，所以取1，則在坐標(0,1)處填1；

A = 1，B = 0 ?-->有視頻 & 無填充子特效時，拍攝鍵要顯示，所以取1，則在坐標(1,0)處填1；

A = 1，B = 1 ?-->有視頻 & 有填充子特效時，拍攝鍵要顯示，所以取1，則在坐標(1,1)處填1；

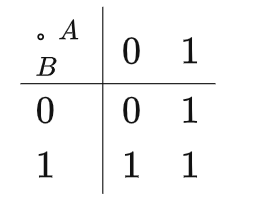
圖5.4  填寫狀態后的卡諾圖

5.3.3 畫卡諾圈

根據上面2.4邏輯相鄰的最小項原則和4.1提到的畫圈原則，把相鄰的 1 圈起來，得到全部的卡諾圈：

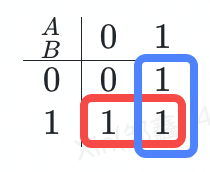
圖5.5  畫出卡諾圈

這個圖里我們得到2個卡諾圈，全部卡諾圈表達式相加，對應寫成邏輯式即得：

A + B

已是最簡表達式，再把符號AB再換回代碼中的變量，有：

(hasVideo || hasSubEffectPhoto)

因為代碼中使用的是 .isHidden?屬性，只要把所得表達式再取反即有 !(A+B)，寫為代碼的邏輯式就是：

takeButton.isHidden = !(hasVideo || hasSubEffectPhoto)

至此我們就得到了這個控件的狀態表達式，在任何時候調用這個刷新方法，就只依賴參數做顯示。

5.3.4 四變量卡諾圖舉例

你可能覺得，上面的變量就兩個，我自己列舉一下也可寫出表達式，不用走卡諾圖。是的恭喜你已發現這個規律，一般2變量我們可以輕易handle，直接計算可能會比畫圖來的簡單。但通過這個做法我們了解其原理與概念之后，現在一起來看個稍微復雜些的，4變量場景的表達式是如何計算的。

就用 特效浮層鍵 的交互狀態來試試吧，對應圖1.1中屏幕左下方那個半透明白色圓形的按鍵，在就緒狀態或視頻暫停狀態下它會出現在拍攝鍵左側：

圖5.6  特效浮層按鍵示意

同樣先來看下計算后的最終結果：

// 特效浮層鍵stickerSelectionButton.isHidden    = !hasVideo && (hasEffect || hasSubEffect) || hasSubEffectPhoto // (!A)(B+C)+D

思考：它在什么情況下需要顯示或隱藏呢？由業務要求[1]可知：是否錄視頻，是否有特效、子特效，是否拍了子特效照片，這幾個參數就能決定其狀態。

于是你問，那音樂參數F呢？我們通過研究具體需求[1]得知，無論有無音樂，都不會影響它的顯示，因此F是個無關參數，計算時不用考慮。當然，你非要把它加進來也行，因為邏輯式化簡后，無關參數都會被消去，不影響結果，這也是“最小項”這個名字的由來：計算出最少相關的參數。要知道，參數越少就越方便我們化簡邏輯式，所以那些一眼看去就無關的參數可以不用加進來。若是計算后發現我們少帶了某個參數或業務要求變化了，則再把它加進來重新計算表達式即可。

• 確定參數

綜上，我們所需參數為ABCD：

let hasVideo      // A: 是否已錄制視頻let hasEffect:    // B: 是否已選有特效let hasSubEffect: // C: 是否帶有子特效let hasSubEffectPhoto // D: 是否已拍照填充了子特效 subEffect

畫出4參數卡諾圖框架：

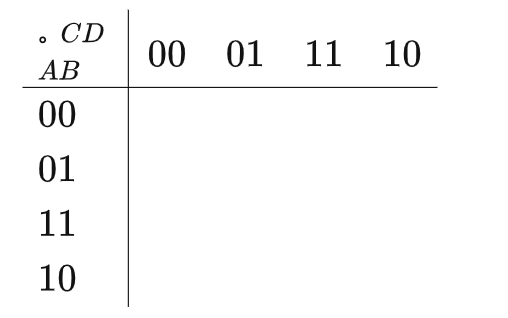
其中AB兩個變量作為列寫在一起，CD兩個作為行寫在一起，變量的順序不是一定的，你也可以換著寫，但格雷碼0和1的位置在表頭是固定的，且最終計算結果也是一樣的。

AB列中，00代表AB取值 A=false; B=false?，01代表取值 A=false; B=true，依此類推。

于是每個格子就對應一個狀態，比如第0行第2列，ABCD取值為0011，代表A=false; B=false; C =true; D=true 這個狀態。所以4變量卡諾圖可以把這些變量全排列的16個狀態都表示出來，不會漏掉某個狀態。

然后對于每個參數狀態，我們思考目標控件的顯示狀態。這里為方便配合使用屬性 .isHidden?，我們定義邏輯填入1為需要隱藏，0為不隱藏?。注意這里與上面例子2變量里的顯示隱藏定義是反相的。參數含義與格子對應，比如，在0011狀態時，代表狀態含義是：

0011 = 無錄視頻，無特效，有子特效，子特效已拍照

本例有個特殊點，因為在需求邏輯上，參數B“無特效”比CD有更高優先級：即無特效時不可能有子特效，也不可能給子特效拍照，所以綜合考慮，在狀態0011時需要顯示控件，即不隱藏，則在0011對應格子里填入0。

• 填充卡諾圖

按照上述方法，把全部16個格子都填上對應(控件需要隱藏)的狀態，AB為列，CD為行：

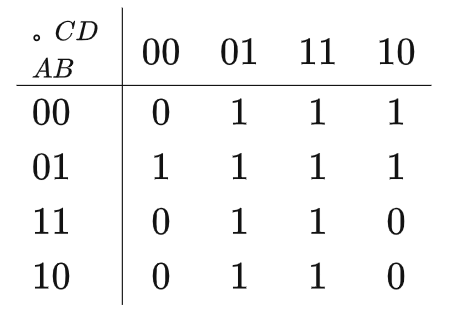
• 按前面 4.2卡諾圈原則 作出全部的卡諾圈，把所有的 1 圈起來：

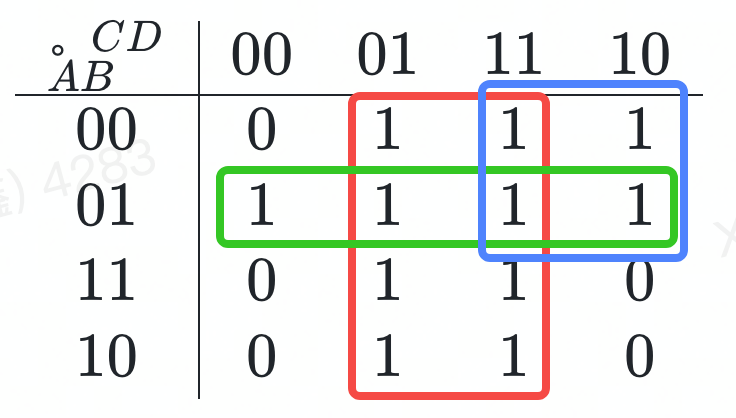
• 化簡

根據卡諾圈寫出邏輯表達式并化簡為最小項表達式（為方便理解，卡諾圈與其表達式用對應的顏色）：

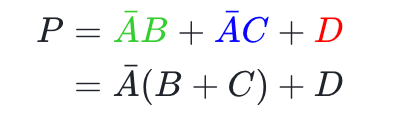
再把符號換回代碼中的變量，即有：

// 特效浮層鍵：!A(B+C)+D
P = !hasVideo && (hasEffect || hasSubEffect) || hasSubEffectPhoto

至此，我們就把變量的邏輯狀態與特效按鍵的狀態對應起來了。

使用此方法的優勢在于：若是需求有變需要更改狀態，則只需要列一遍參數，重新畫卡諾圖計算表達式即可，修改的地方也只有這一行的邏輯式，而不會影響其他控件的邏輯，也不用再走一遍改動后的業務流程。

6、拓展：五變量卡諾圖

五變量以下最多十六方格，也可用上述方法解出得到。但在實際開發中極少需要到5變量，掌握4變量方法已足夠應對大多數場景。此處僅作拓展了解。六變量以上方格過多，用此方法反倒麻煩[3]。

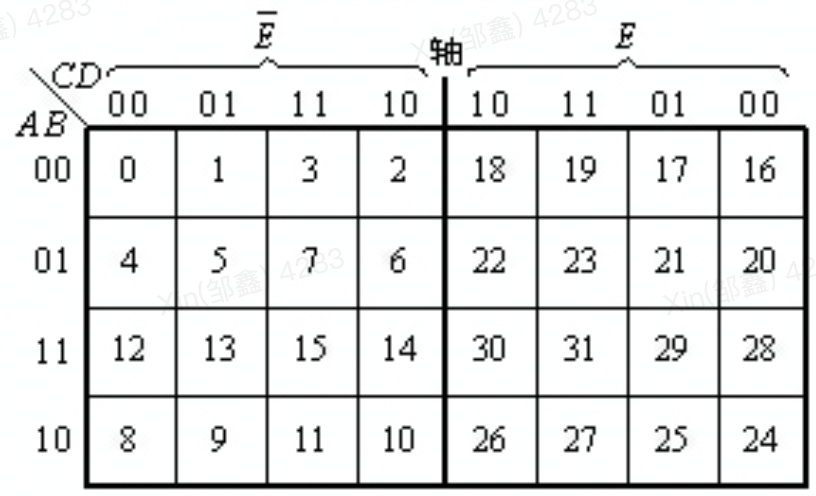
圖6.1  五變量卡諾圖

它是由四變量最小項圖構成的，將左邊的一個四變量卡諾圖按軸翻轉 180 °而成。左邊的一個四變量最小項圖對應變量 E =0 ，軸左側的一個對應 E =1 。

這樣一來除了幾何位置相鄰的小方格滿足鄰接條件外，以軸對稱的小方格也滿足鄰接條件，這一點需要注意。圖中最小項編號按變量高低位的順序為 EABCD 排列時，所對應的二進制碼確定。

此時要注意列上變量排列的左右對稱關系，對于既不含 E非也不含 E 的與項，可以填入 E非四變量卡諾圖中然后以中間軸翻轉 180 °，在 E 四變量卡諾圖中對稱位置也填上“ 1 ”。

五變量邏輯式化簡的舉例說明如下，每個步驟原理在上文已作詳盡說明，此處不再贅述：

化簡下式：

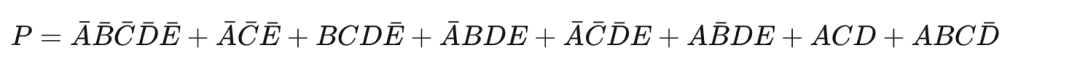
• 填入卡諾圖：

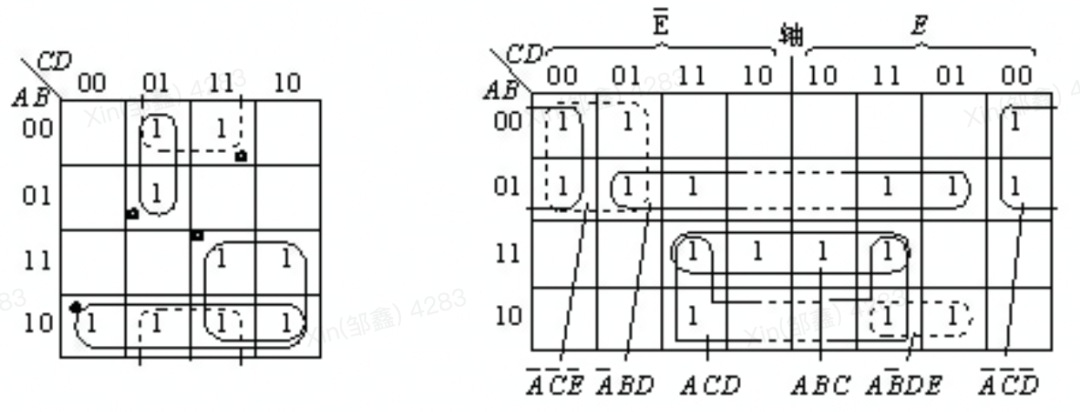
• 作卡諾圈：

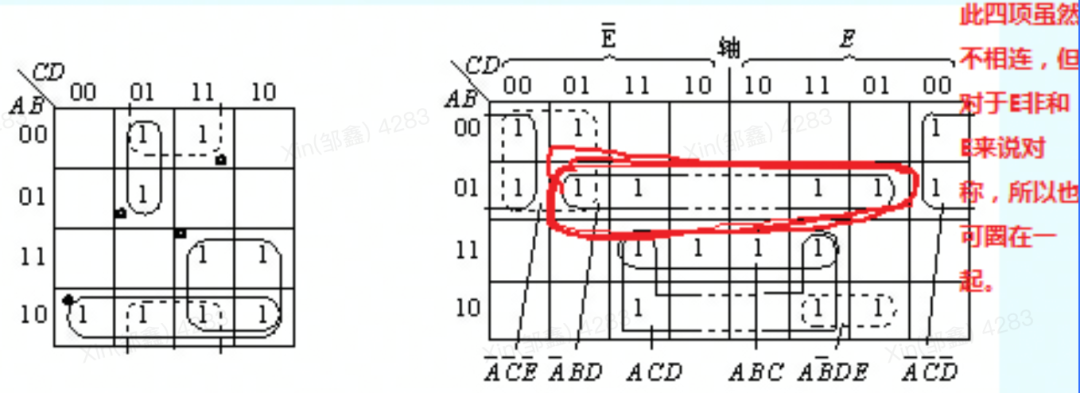
合并與化簡得：

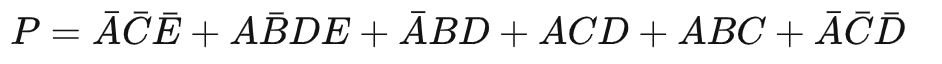
7、小結

我們簡要介紹了卡諾圖原理與其化簡方法，這個工具和思想可以用在任何多參數有競爭或多種情況的場景下決定某個操作是否執行。這個方法在參數較多且狀態復雜時使用，若邏輯狀態較簡單，則可直接用表達式寫出，代碼邏輯力求更清晰明了。

在上述場景的操作流程中，任何時候調用這個刷新方法，我們都可獲得符合當下參數的頁面狀態，因為交互就只依賴參數做顯示，而不需要考慮其前置狀態。

卡諾圖邏輯化簡法優點有：簡化了多參數多控件等復雜情況下邏輯與方法難以直觀處理的情況，且在后續維護迭代中，也可獨立地修改某個控件的刷新邏輯，不用擔心影響其他控件或業務流程，每個交互的控件狀態修改簡易靈活，方便計算。

同時，卡諾圖的使用也有其局限性，它比較適合4變量或以下的場景，在5變量及以上用此方法反而復雜，且在實際開發中，4變量場景已然是比較少見，則此法已足夠我們處理大多數2~4變量的交互邏輯情況了。

Reference

[1] https://blog.shizhuang-inc.com/article/Nzc4Ng==

[2] https://blog.csdn.net/wangqinyi574110/article/details/116573015

[3] https://www.cnblogs.com/uiojhi/p/7517732.html

[4] https://zhuanlan.zhihu.com/p/158535749

[5] https://www.cnblogs.com/iBoundary/p/11303861.html

[6] https://www.pudn.com/news/6367746ba4b7e43a5e898044.html

[7] https://zhuanlan.zhihu.com/p/268750530