做了那么久程序員，二進制計算都會用了嗎？

作者：小傅哥 2023-01-10 11:58:24

從畢業(yè)入職公司看大佬的代碼出現(xiàn) 2 << 4 開始？從小白晉升高開讀框架的源碼看到 MAXIMUM_CAPACITY = 1 << 30; 開始？還是從什么時候開始？

一、前言

你是什么時候注意到位運算？

從畢業(yè)入職公司看大佬的代碼出現(xiàn) 2 << 4 開始？從小白晉升高開讀框架的源碼看到 MAXIMUM_CAPACITY = 1 << 30; 開始？還是從什么時候開始？

其實二進制的位運算一直在我們那身邊，從你開始編寫 Hello Word 打印輸出時就有二進制流的處理，只不過隱藏的很深不好發(fā)現(xiàn)。所以在我們開始意識到代碼和二進制的關(guān)系往往都是來自于看到可以用二進制完成的計算，包括；二進制計算效率高于乘機，也包括二進制可以更好的體現(xiàn)出你要設(shè)置值的大小范圍。比如你要設(shè)定一個指定范圍大小的 Int 值 = 1073741824，那么是給這樣一個整數(shù)值看起來直觀，還是二進制 1<< 30 更直觀呢？其實他們兩個值是相等的。所以這樣的情況下也會有二進制運算的體現(xiàn)。

而小傅哥在學(xué)習編程階段，第一次注意到二進制的運算是關(guān)于a、b兩個值的互換，如果不引入第三個值就可以完成？

int a = 2, b = 3;
a = a ^ b;
b = a ^ b;
a = a ^ b;

一個 ^ 帽子一樣的運算符，就把兩個數(shù)給替換，替換后 a = 3，b = 2 那它是怎么辦到的呢？

?^ 異或運算：兩個操作數(shù)的同位中，如果值相同（都是 0 或者都是 1）則為 0，不同（一個是 0，一個是 1）則為 1

以二進制數(shù)據(jù)為基礎(chǔ)進行運算解析 a = 2 二進制數(shù)為 0010、b = 3 二進制數(shù)為 0011a = a ^ b = 0010 ^ 0011 = 0001b = a ^ b = 0001 ^ 0011 = 0010 = 2a = a ^ b = 0001 ^ 0010 = 0011 = 3
異或運算的基本定理解析 a = a ^ bb = a ^ b = a ^ b ^? b = a = 2a = a ^ b = a ^ a ^ b = b = 3

而二進制的運算魅力還遠不至于此，還可以完成奇偶判斷、有效位計算、乘法、加法等。這些內(nèi)容的學(xué)習可以讓我們研發(fā)人員，積累編程邏輯和拓展思維模式。接下來小傅哥就帶著大家學(xué)習一下。

二、位操作介紹

位操作是程序設(shè)計中對位數(shù)組或二進制數(shù)的一元和二元操作。在許多古老的微處理器上，位運算比加減運算略快，通常位運算比乘除法運算要快很多。在現(xiàn)代架構(gòu)中，位運算的運算速度通常與加法運算相同（仍然快于乘法運算），但是通常功耗較小，因為資源使用減少。

四種基本的位運算包括；與&、或|、非~、異或^

int a = 1; // 0001
int b = 2; // 0010
int c = 4; // 0100
int d = 8; // 1000
int e = 15;// 1111

// 與運算；0001
System.out.println(Integer.toBinaryString(a & e)); // 0001
// 或運算；0011
System.out.println(Integer.toBinaryString(a | b)); // 0011
// 異或運算；0101
System.out.println(Integer.toBinaryString(a ^ c)); // 0101
// 非運算；...11110111
System.out.println(Integer.toBinaryString(~d));

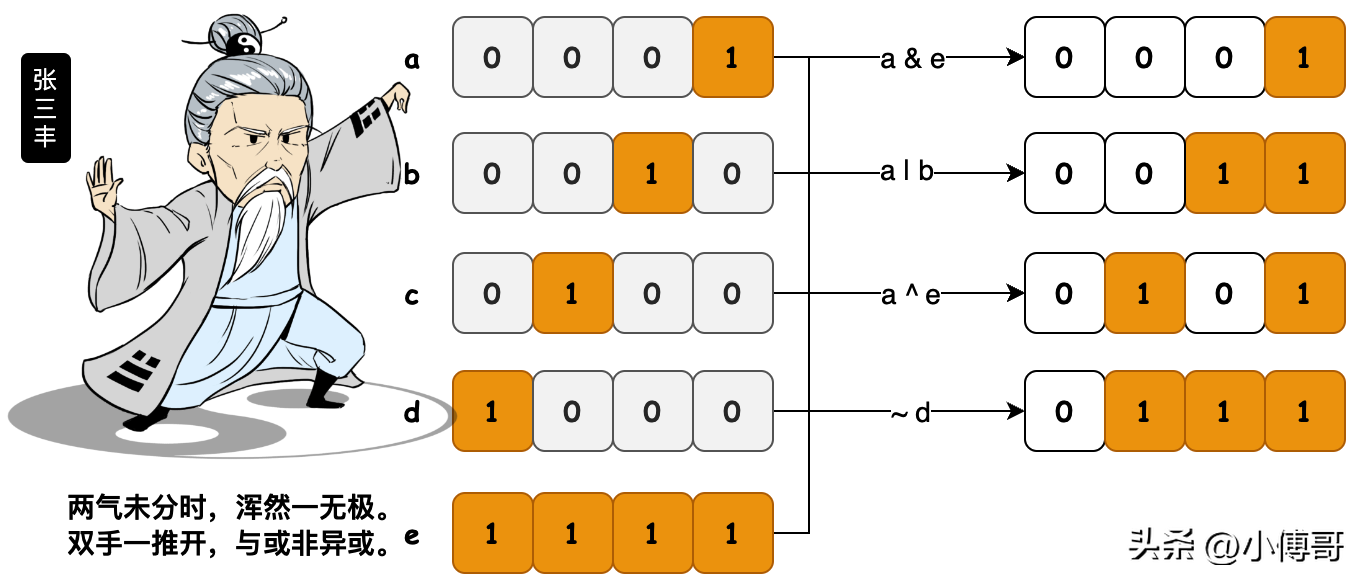
與運算；兩個數(shù)都轉(zhuǎn)為二進制，然后從高位開始比較，如果兩個數(shù)都為1則為1，否則為0。
或運算；兩個數(shù)都轉(zhuǎn)為二進制，然后從高位開始比較，兩個數(shù)只要有一個為1則為1，否則就為0。
非運算；如果位為0，結(jié)果是1，如果位為1，結(jié)果是0。
異或運算；兩個數(shù)轉(zhuǎn)為二進制，然后從高位開始比較，如果相同則為0，不相同則為1。

三、位運算案例

1. 獲取位值

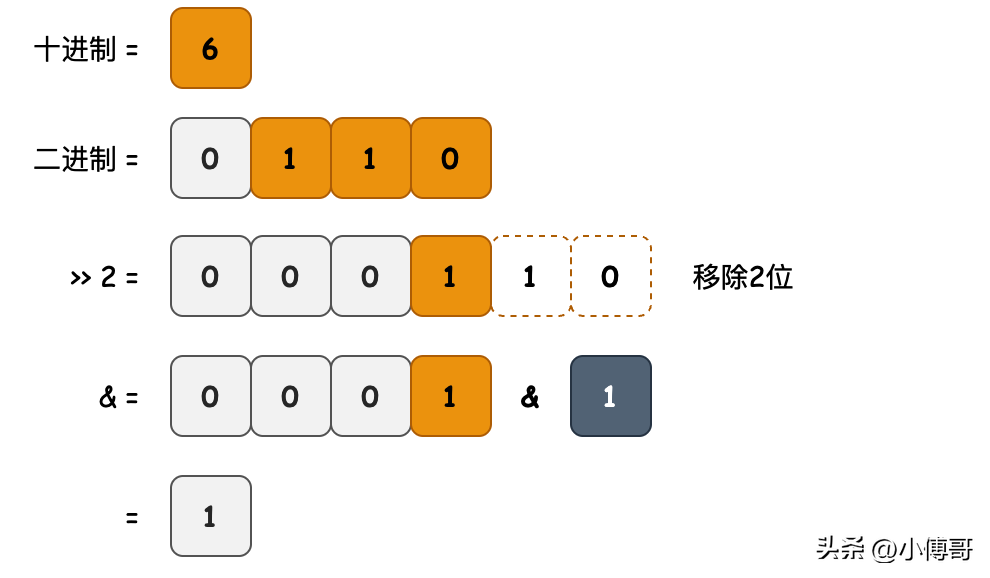
public int getBit(int number, int bitPosition){
    return (number >> bitPosition) & 1;
}

目的：獲取二進制數(shù)字中，指定位置的值。
邏輯：該方法將目標值右移到最右邊，即位數(shù)組的第0個位置上，如；0001 的二進制形式。之后與 1 進行與操作。如果目標位是1，那么結(jié)果就是1，反之結(jié)果是0；

2. 設(shè)置位值

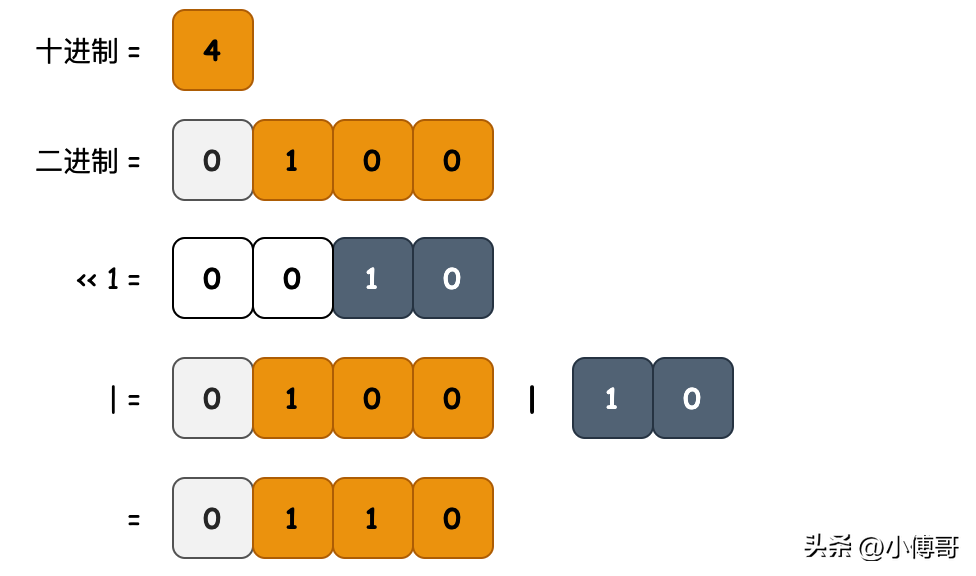
public int setBit(int number, int bitPosition){
    return number | (1 << bitPosition);
}

目的：設(shè)置二進制數(shù)字中，指定位置的值
邏輯：1 就像一個子彈，左移指定位數(shù)到目標位置，如；0010 的二進制形式。與目標值 number 做或運算(把子彈打進去)，設(shè)置結(jié)果并返回。

3. 清空位值

public int clearBit(int number, int bitPosition){
    int mask = ~(1 << bitPosition);
    return number & mask;
}

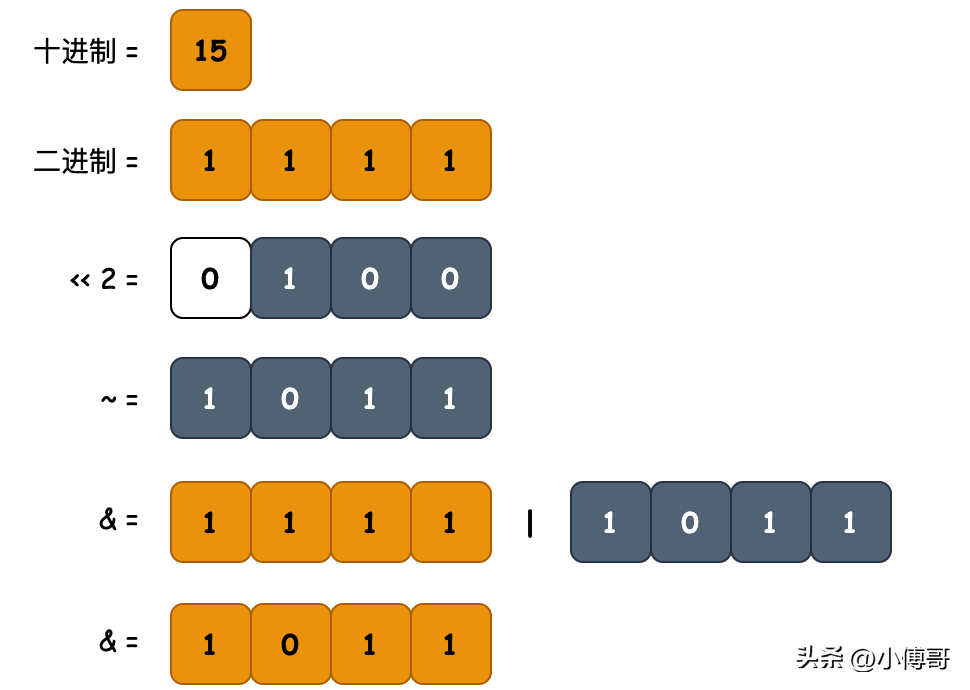
目的：清空二進制數(shù)字中，指定位置的值
邏輯：類似于設(shè)置位值，把1左移指定位數(shù)后取反，從 0010 得到 1101 并與目標值 number 做與&運算，清掉目標位的值。

4. 更新位值

public int updateBit(int number, int bitPosition, int bitValue){
    int clearMask = ~(1 << bitPosition);
    return (number & clearMask) | (bitValue << bitPosition);
}

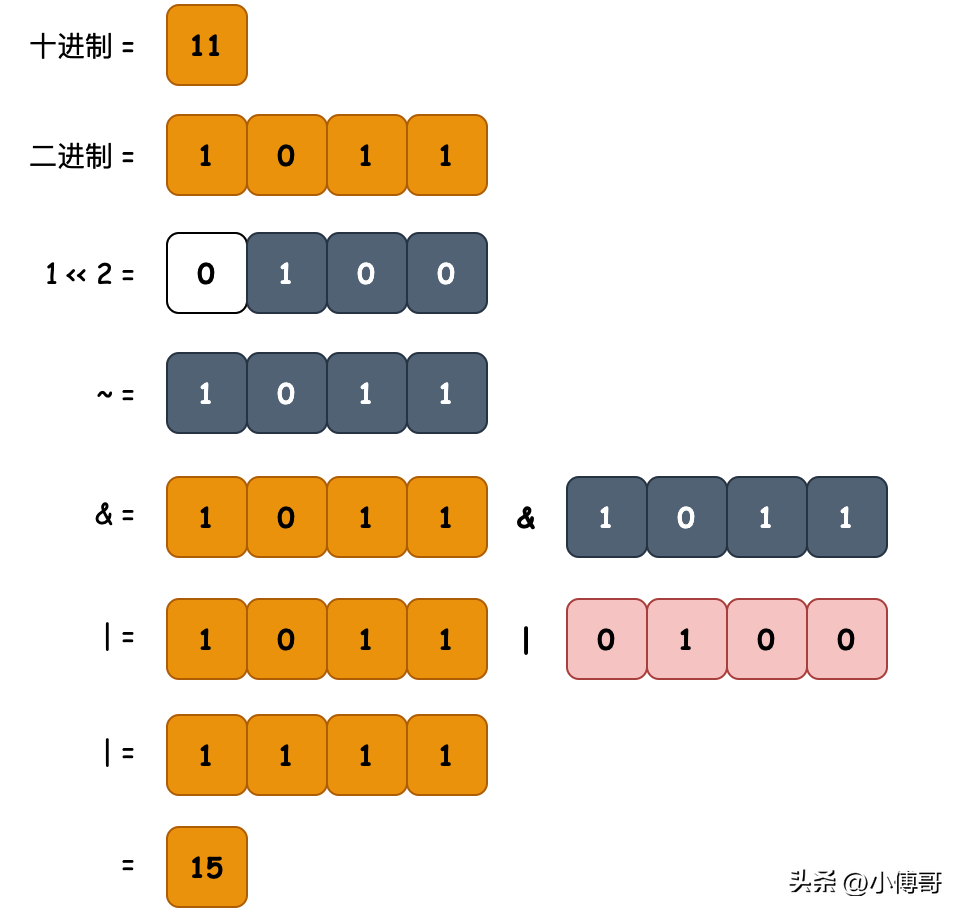
目的：清空二進制數(shù)字中，指定位置的值
邏輯：結(jié)合清空clearBit、設(shè)置setBit，兩個方法將制定位置替換為設(shè)置值。

5. 偶數(shù)判斷

public boolean isEven(int number){
    return (number & 1) == 0;
}

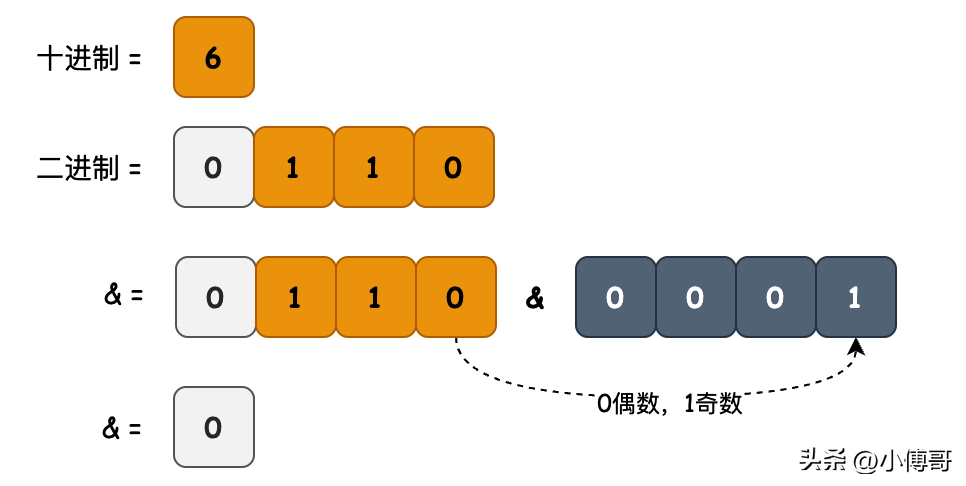
目的：檢測 number 是否為偶數(shù)
邏輯：檢測二進制的最右側(cè)一位，如果是1，那么一定是奇數(shù)。所以可以與1做與&運算的結(jié)果和0判斷。不等于0是奇數(shù)，等于0是偶數(shù)。

6. 正數(shù)判斷

public boolean isPositive(int number) {
    if (number == 0) {
        return false;
    }
    return ((number >> 31) & 1) == 0;
}

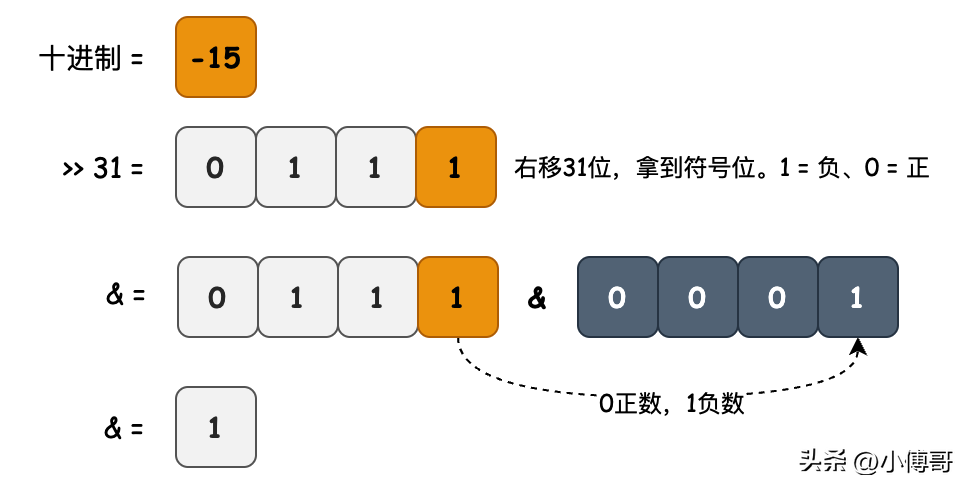
目的：判斷 number 值是否為正數(shù)。
邏輯：基于二進制正數(shù)最左邊的值是0的這個事實，右移31位，和1做與&運算，如果結(jié)果等于1為負數(shù)，反正為正數(shù)。

7. 左移乘二

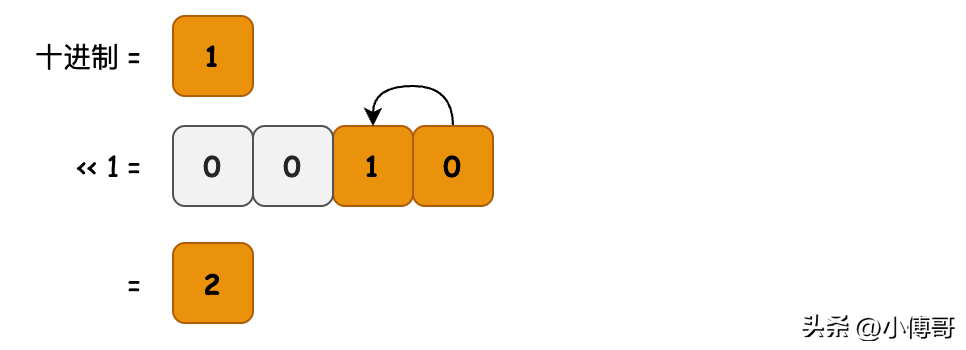
public int multiplyByTwo(int number){
    return number << 1;
}

目的：乘以2
邏輯：該方法將原始數(shù)字向左移動一位。因此所有位都將乘以2，因此數(shù)字本身也將乘以2。

8. 右移除二

public int divideByTwo(int number){
    return number >> 1;
}

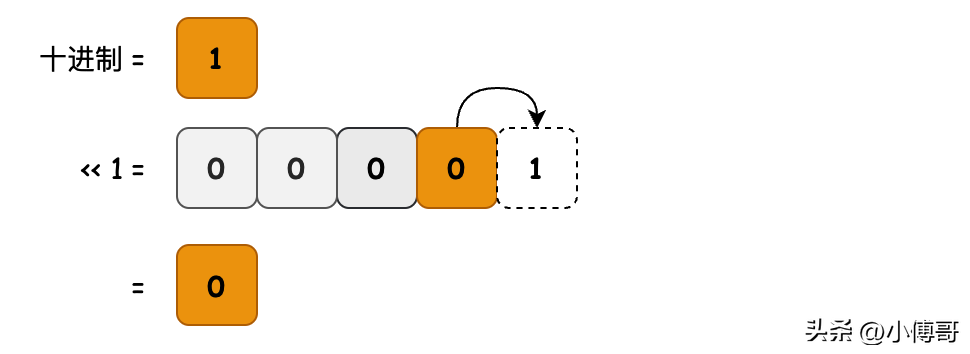
目的：除以2
邏輯：該方法將原始數(shù)字向右移動一位。因此所有位都將除以2，因此數(shù)字本身也將除以2,且不會產(chǎn)生余數(shù)。

9. 正負交換

public int switchSign(int number){
    return ~number + 1;
}

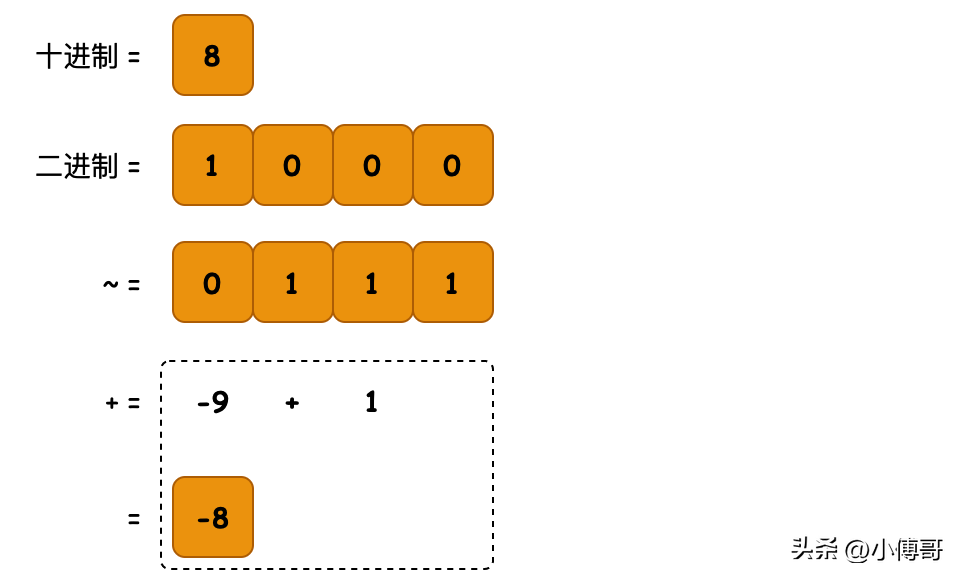
目的：正數(shù)轉(zhuǎn)負數(shù)，負數(shù)轉(zhuǎn)正數(shù)
邏輯：通過二進制取反運算，如 1000 = 8 取反 1.....0111 = -9 + 1 = -8

10. 乘法運算(有符號)

public int multiply(int a, int b) {
    int multiply = 0;
    while (a != 0 && b != 0) {
        System.out.print("計算步驟(" + (isEven(b) ? "偶數(shù)" : "奇數(shù)") + ")：a(" + String.format("%04d", Integer.valueOf(Integer.toBinaryString(a))) + ") = " + a + " | b(" + String.format("%04d", Integer.valueOf(Integer.toBinaryString(b))) + ") = " + b);
        // b 是偶數(shù)：2a * (b/2)
        if (isEven(b)) {
            a = multiplyByTwo(a);
            b = divideByTwo(b);
        }
        // b 奇數(shù)
        else {
            // b 正數(shù)：2a * (b - 1)/2 + a
            if (isPositive(b)) {
                multiply += a;
                a = multiplyByTwo(a);
                b = divideByTwo(b - 1);
            }
            // b 負數(shù)：2a * (b + 1)/2 - a
            else {
                multiply -= a;
                a = multiplyByTwo(a);
                b = divideByTwo(b + 1);
            }
        }
        System.out.println(" | multiply(" + String.format("%04d", Integer.valueOf(Integer.toBinaryString(multiply))) + ") = " + multiply);
    }
    return multiply;
}

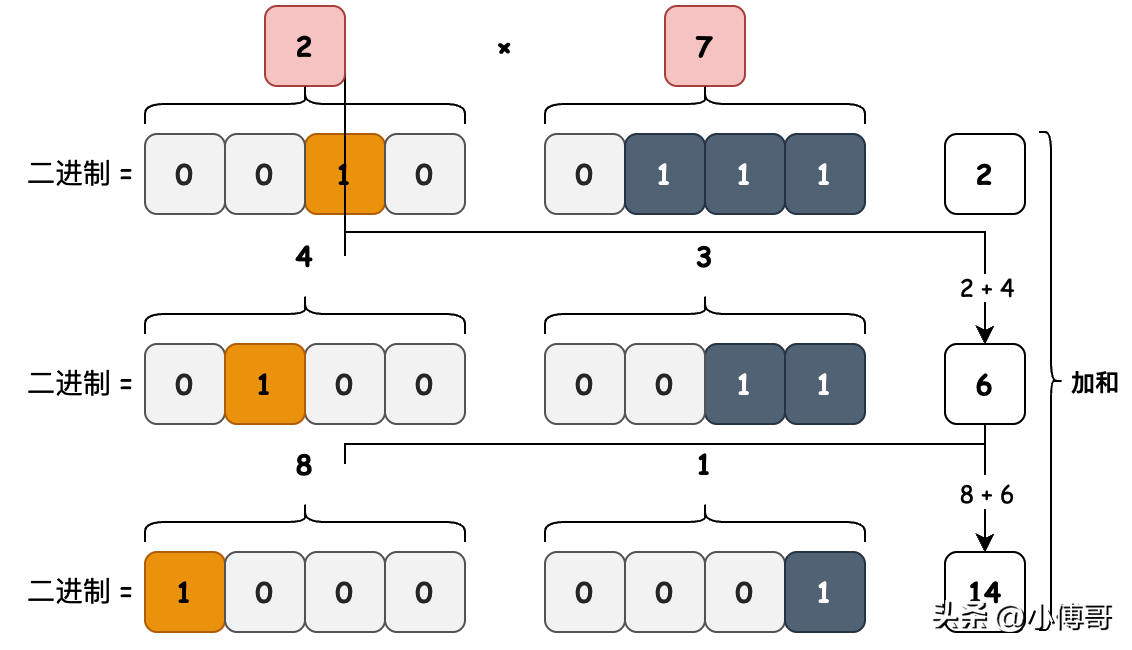
目的：計算有符號二進制乘積
公式：推到公式與代碼向?qū)?yīng)= a * b= 2a * (b/2) —— b為偶數(shù)= 2a * (b - 1)/2 + a —— b 為奇數(shù)、正數(shù)= 2a * (b + 1)/2 - a —— b 為奇數(shù)、負數(shù)
邏輯：乘數(shù)a不斷左移、乘數(shù)b不斷右移。當b歸0時，a左移累計下來的值就是乘積總和。如圖

11. 乘法運算(無符號)

public int multiplyUnsigned(int number1, int number2) {
    int result = 0;
    int multiplier = number2;
    int bitIdx = 0;
    while (multiplier != 0) {
        if ((multiplier & 1) == 1) {
            System.out.println(number1 + " << " + bitIdx + " = " + (number1 << bitIdx));
            result += number1 << bitIdx;
        }
        bitIdx += 1;
        multiplier = multiplier >> 1;
    }
    return result;
}

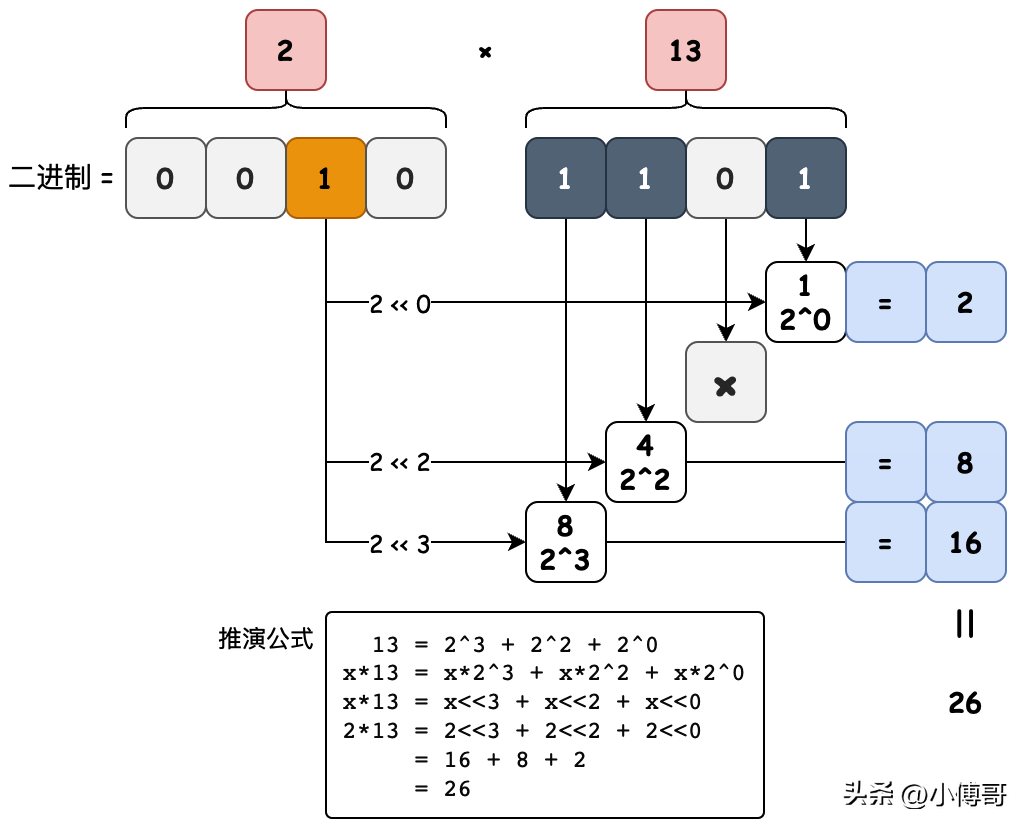
目的：計算無符號二進制乘積
公式：13 = 2^3 + 2^2 + 2^0x*13 = x*2^3 + x*2^2 + x*2^0x*13 = x<<3 + x<<2 + x<<02*13 = 2<<3 + 2<<2 + 2<<0 = 16 + 8 + 2 = 26
邏輯：每個數(shù)字都可以表示成一系列2的冪之和。例如 13 的二進制是 1101，最右側(cè)第1位1，是2的0次冪，所以對應(yīng)2的進制值是左移0位。再比如13的右數(shù)第3位是1，對應(yīng)位置值是4也就是2的2次冪，所以對應(yīng)2的進制值是左移2位。最終把這些值相加就是乘積值。

12. 一的數(shù)量

public int countSetBits(int originalNumber){
    int setBitsCount = 0;
    int number = originalNumber;
    while (number != 0) {
        setBitsCount += number & 1;
        number >>>= 1;
    }
    return setBitsCount;
}

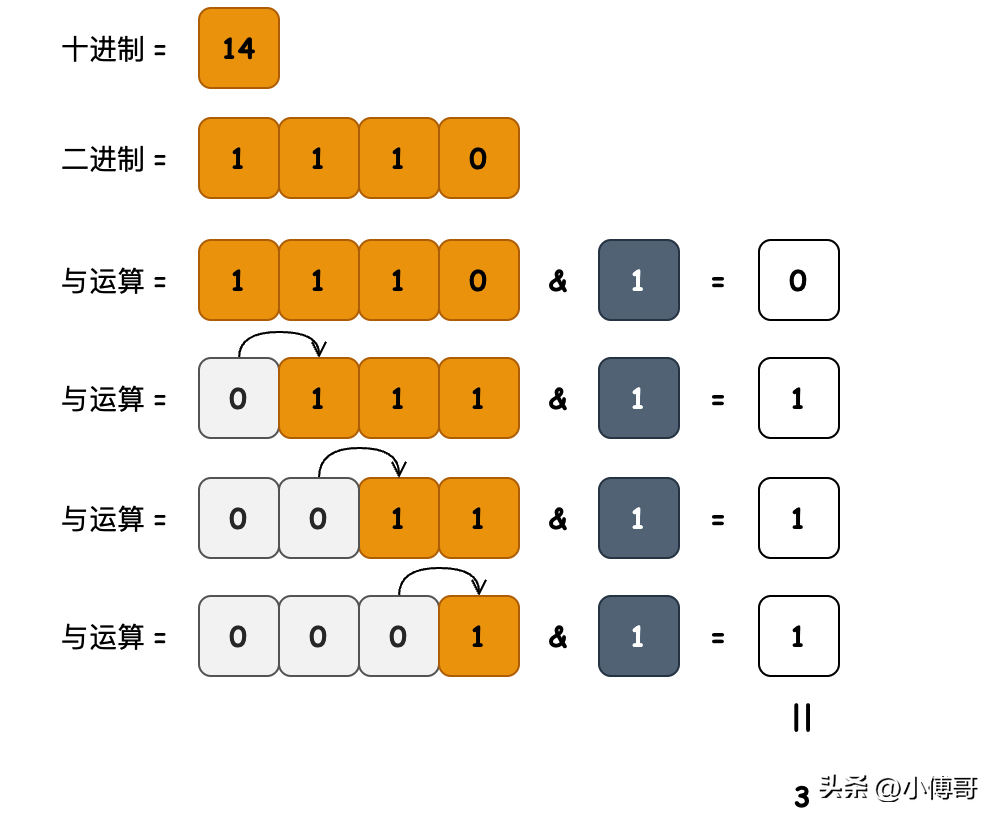
目的：使用位運算符對一個數(shù)字里設(shè)置為1的位進行記數(shù)
邏輯：把數(shù)字每次向右移動1位，然后使用&操作符取出最右邊一位的值，1則記數(shù)加1，0則不計。

13. 轉(zhuǎn)換計算

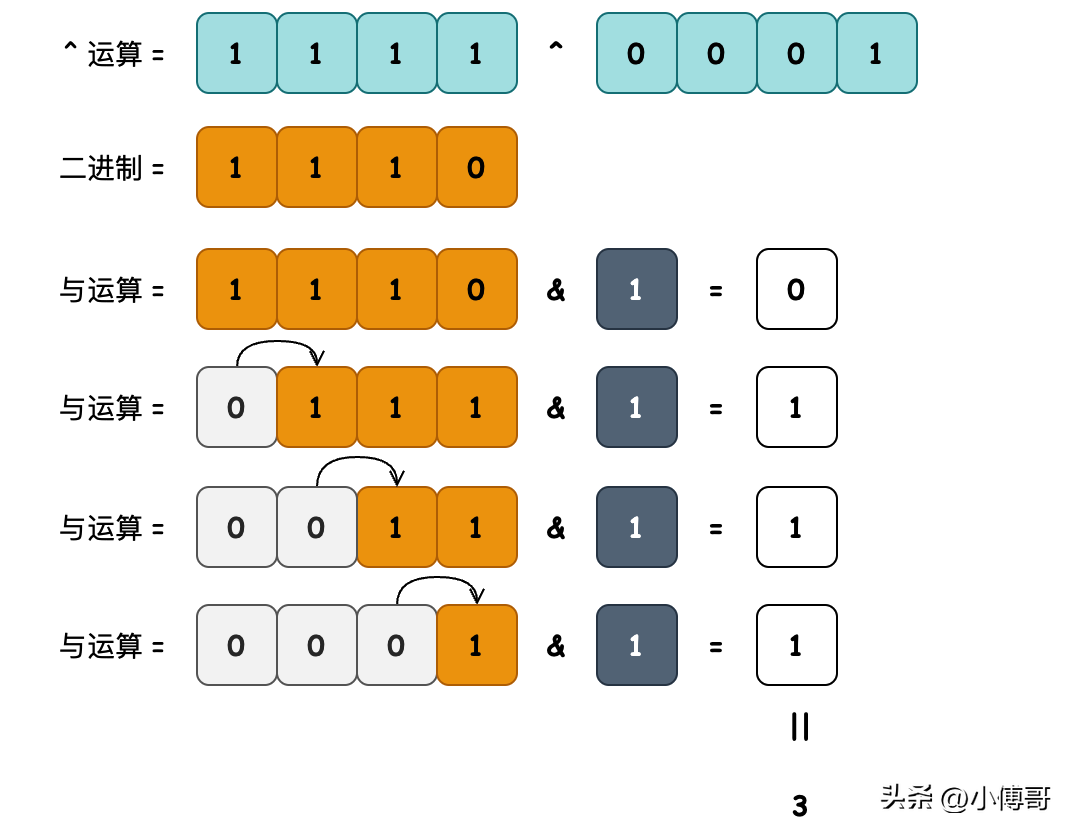
public int bitsDiff(int number1, int number2){
    return countSetBits(number1 ^ number2);
}

目的：計算一個數(shù)字，轉(zhuǎn)換為另外一個數(shù)字，所需要的轉(zhuǎn)換位數(shù)。
邏輯：當數(shù)字進行XOR異或運算時，結(jié)果將是不同位數(shù)的數(shù)量(即異或的結(jié)果中所有被設(shè)置為1的位的數(shù)量)。

14. 有效位數(shù)

public int bitLength(int number){
    int bitsCounter = 0;
    while ((1 << bitsCounter) <= number) {
        bitsCounter += 1;
    }
    return bitsCounter;
}

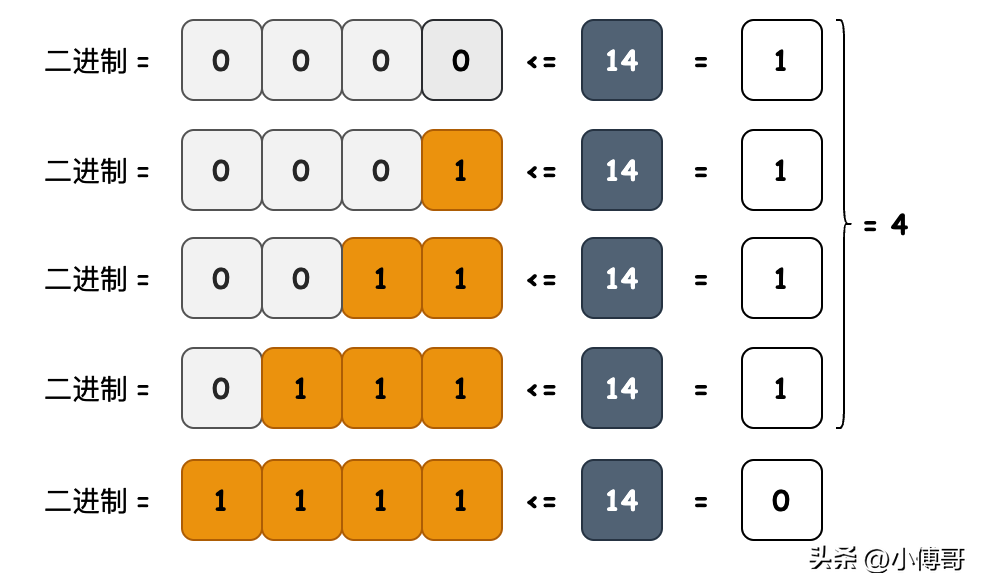
目的：計算二進制數(shù)值的有效位數(shù)，例如 14 = 1110 有效位為4位。
邏輯：通過1不斷地左移加和與 number 做對比，只要比number小就累加1位。

15. 冪值判斷

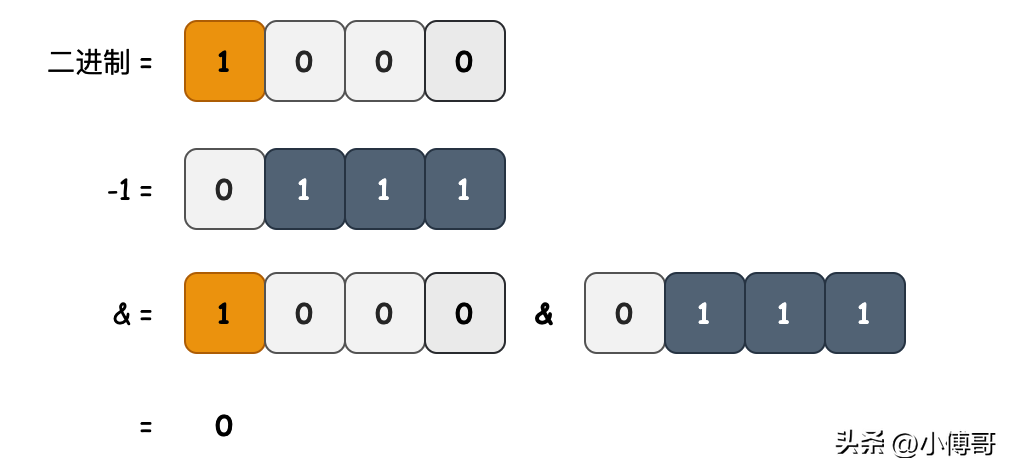
public boolean isPowerOfTwo(int number) {
    return (number & (number - 1)) == 0;
}

目的：檢查number是否為2的冪值。
邏輯：2的冪值形式的數(shù)字為2、4、8、16 等，那么可以把一個二進制數(shù)進行錯位與&運算，如果錯位比對都為0，那么就是2的冪數(shù)。

16. 加法運算(Ripple-carry adder)

public int fullAdder(int a, int b) {
    int result = 0;
    // 計算每次的進位值，1 + 1 = 0010 進位為1。是一種&運算。
    int carryOut = 0;
    System.out.println("| aBit | bBit | carryIn | aiPlusBi | bitSum | carryOut | result |");
    for (int i = 0; i < 32; i++) {
        int aBit = getBit(a, i);
        int bBit = getBit(b, i);
        int carryIn = carryOut;
        System.out.print("|   " + aBit + "  |  " + bBit + "   |       " + carryIn);
        // 加和 - 兩個值；如果相同則為0，不相同則為1
        int aiPlusBi = aBit ^ bBit;
        System.out.print(" |        " + aiPlusBi);
      
        // 加和 - 進位；
        int bitSum = aiPlusBi ^ carryIn;
        System.out.print(" |      " + bitSum);
      
        // 進位；同位置 ai & bi = 1 | 與進位 aiPlusBi & carryIn = 1
        carryOut = (aBit & bBit) | (aiPlusBi & carryIn);
        System.out.print(" |  " + carryOut + "(" + Integer.toBinaryString(carryOut) + ")   ");
      
        // 累加；把當前位置計算的值，左移n位
        result = result | (bitSum << i);
        System.out.println(" | " + result + "(" + String.format("%04d", Integer.valueOf(Integer.toBinaryString(result))) + ")|");
    }
    return result;
}

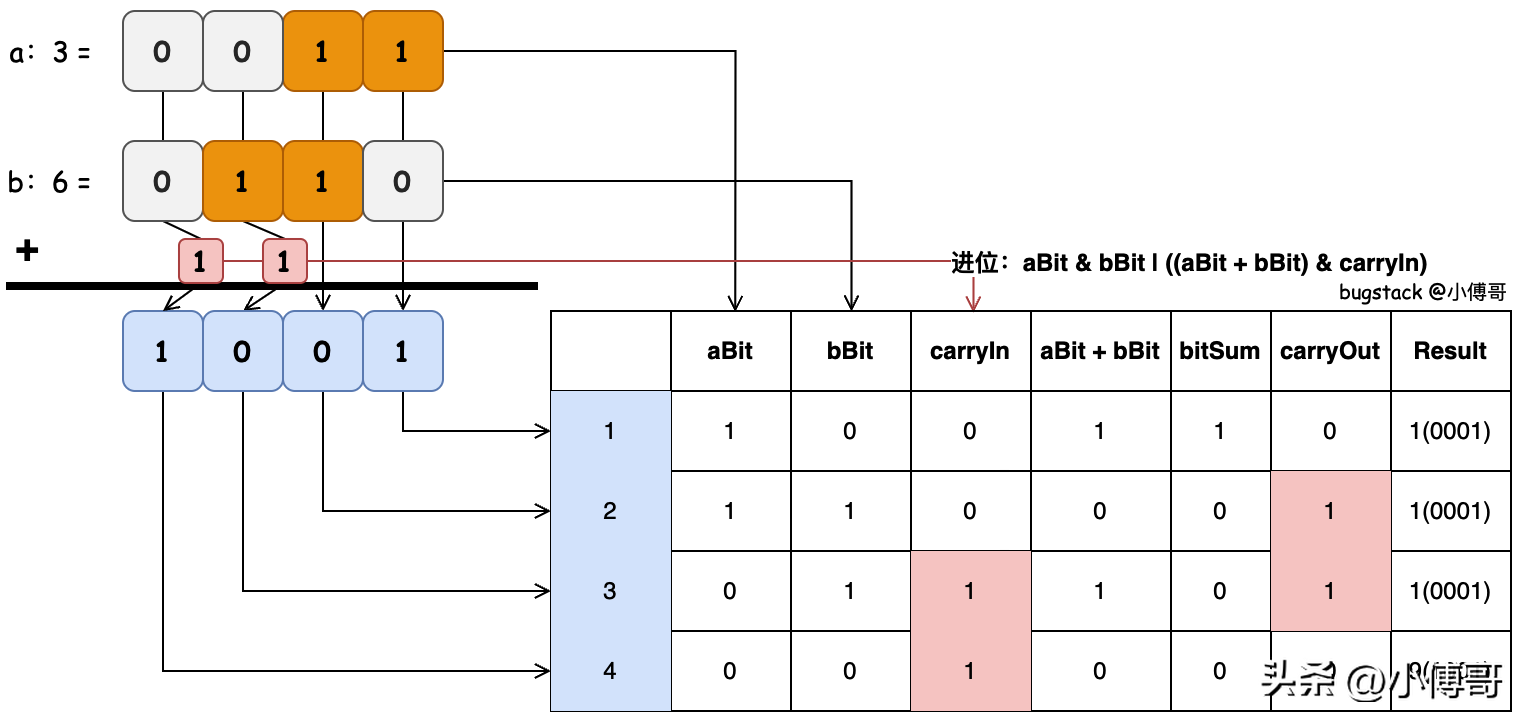
目的：計算有符號二進制加法
邏輯：二進制的累加可以對照下計算10進制累加時一樣，對應(yīng)2個數(shù)字相加，當有進位的時候記錄進位。首先二進制的加和計算，1+1 = 10、1+0=01、0+1=01、0+0=00，那么正好對應(yīng)上 ^ 非運算，相同則為0，不相同則為1，因為即使兩個1相加，當前位的值也是0。之后是進位相加，兩數(shù)想加后，還可能有進位上來的數(shù)值與兩數(shù)進行相加。結(jié)果相加完成后，計算進位，并保留進位用于下次計算。進位的計算為；ai & bi = 1 | 與進位 aiPlusBi & carryIn = 1，無論是兩數(shù)相加，還是兩數(shù)的和 aiPlusBi 與進位相加，只要與運算是1，那么就要保留進位。最后是累加結(jié)果，把對應(yīng)位置的結(jié)果計算，按照當前計算到到二進制的位數(shù)左移到目標為止，累加到 result，最后就是結(jié)果值。

四、常見面試題

& 和 ~ 是什么運算？
兩數(shù)交換不引入第三個變量如何處理？
二進制中1個個數(shù)怎么計算？
實現(xiàn)一個兩數(shù)加和？
實現(xiàn)一個無符號兩數(shù)成績？

責任編輯：武曉燕來源：今日頭條

二進制運算計算

成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看