大家好，我是前端西瓜哥。

最近更文比較少，是因為本人在做個人開源項目，用 Canvas 做一個設計工具，做個乞丐版 figma。期間遇到了不少問題，在這里記錄一下。

今天開始會恢復高頻更新的，一兩天一更。內容主要會圍繞我打造的設計工具遇到的一些問題和解決方案，也會有其他主題。

項目地址：

https://github.com/F-star/suika

線上體驗：

https://blog.fstars.wang/app/suika/

元素和它的包圍盒（bBox）

元素指的是一些圖形，比如矩形、橢圓。

為了方便描述，后面都會用矩形作為例子。

元素有一個包圍盒（Bounding Box），是能包裹元素的最小矩形。當然大一點也行，但必須能包裹元素。

const bBox = {
  x: 100,
  y: 100,
  width: 30,
  height: 40
}

x 和 y 代表包圍盒的位置，width 和 height 代表盒子的尺寸。

另外元素一個 rotation 屬性，表示元素以其中心位置（即包圍盒的正中心）的旋轉弧度。

bBox 是考慮旋轉的（最外層的矩形）：

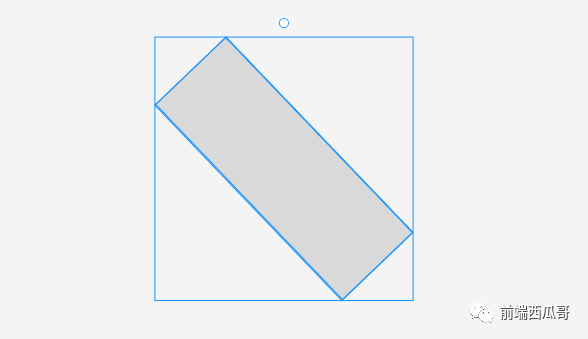
bBox

還有一種不考慮旋轉，我暫且稱其為 bBoxWithoutRotation。它會忽視 rotation 的存在，得到一個旋轉前的 bBox。我們使用它配合渲染層（ctx.rotate(angle)），繪制一個進行了旋轉的盒子。

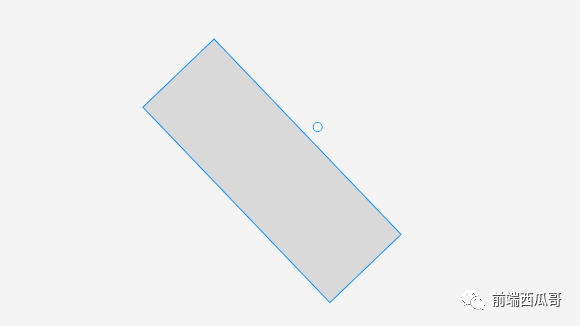
bBoxWithoutRotation

選中元素

選中的元素需要分兩種情況討論，一種是選中單個元素，一種是選中多個元素。

對于單個元素，要繪制 bBoxWithoutRotation。原因是只有一個元素，也就一個旋轉角度，旋轉起來更能表現這個元素的情況。見下圖：

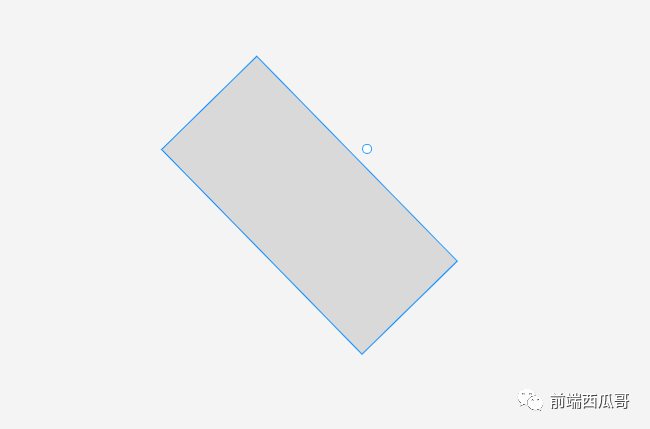
對于多個元素，情況則不同了，因為不同的元素有不同的旋轉角度，所以要計算所有元素的 bBox，然后取出其中最小的 x、y 和最大的 x、y，組成包圍所有元素的選中框：

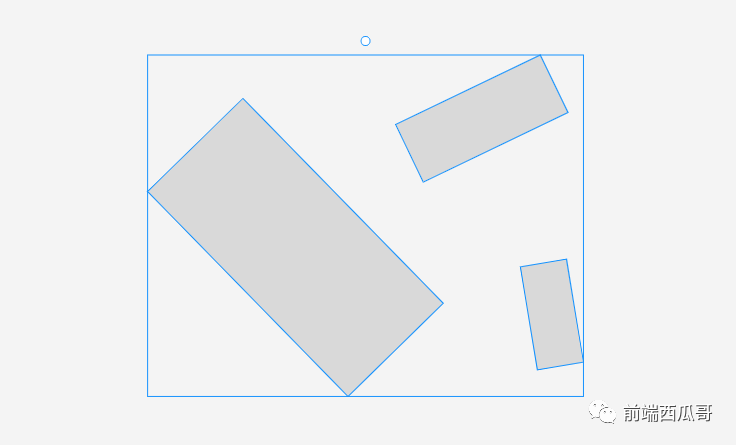
旋轉元素

旋轉元素同樣分兩種情況討論：旋轉單個元素，以及旋轉多個元素。

先講解 旋轉單個元素。我們看看效果：

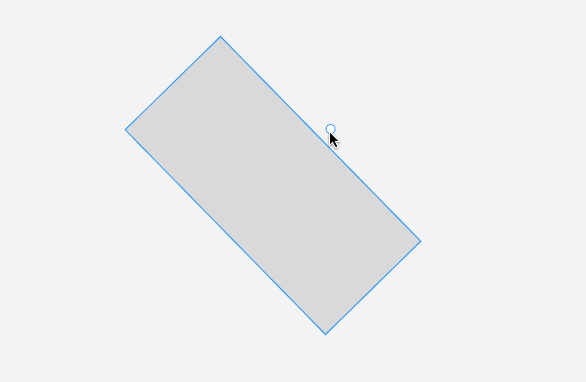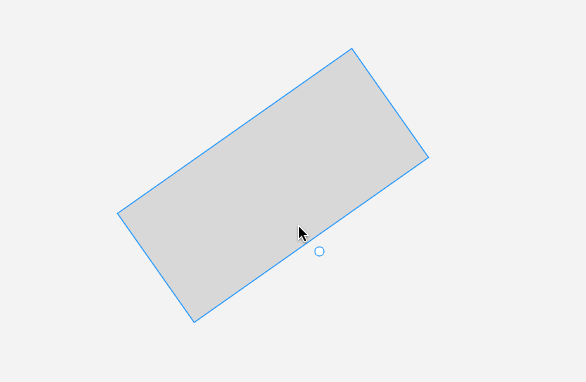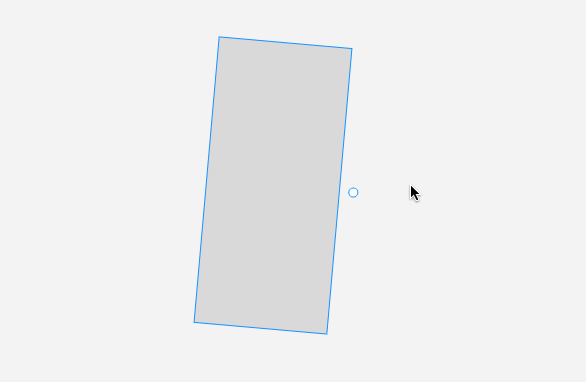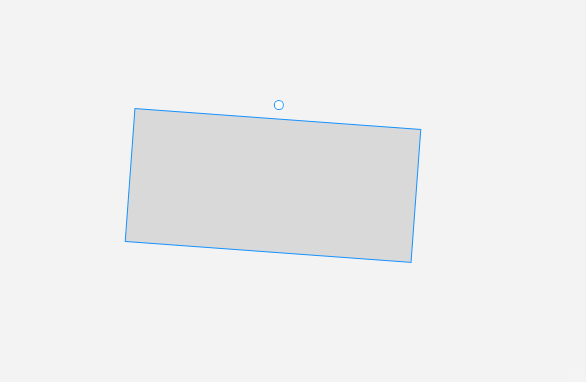
旋轉單個元素

首先，從圖形的中點連接光標位置，得到一個向量。我們的旋轉角度就是這個向量和向上向量（即 [0, -1]）的夾角。

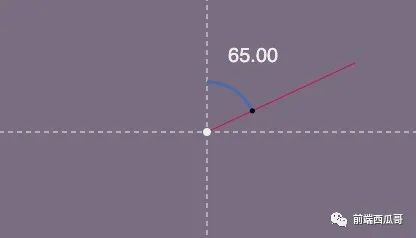
求向量角度

這里我們可以用 點積公式 來計算這個夾角。

計算好這個夾角，將其賦值給選中的元素的 rotation 屬性，然后進行渲染，讓渲染引擎根據新的角度進行繪制。

然后是 旋轉多個元素。效果：

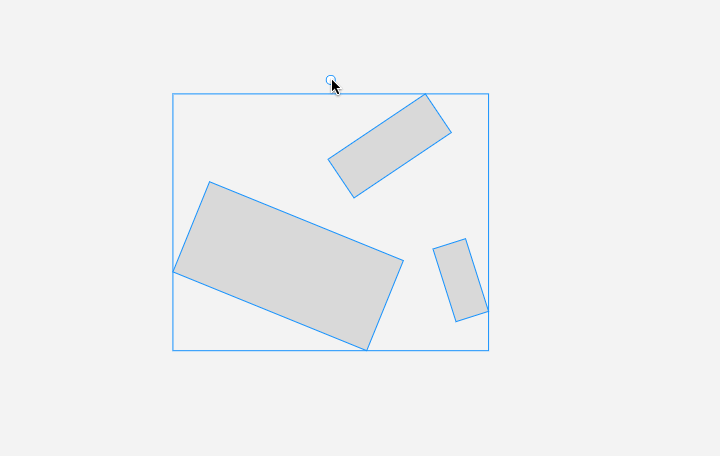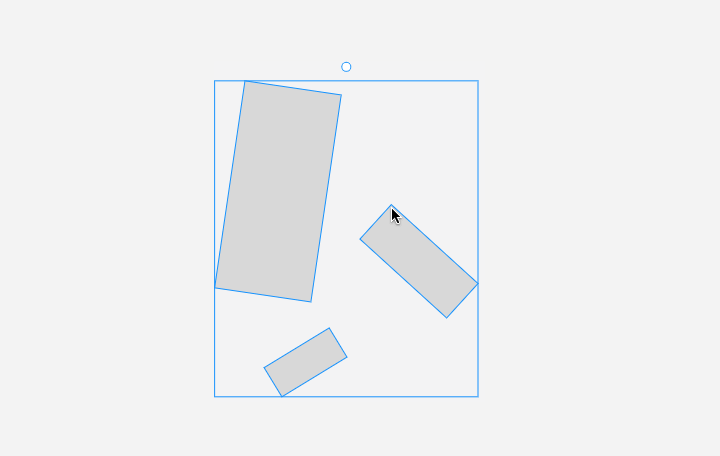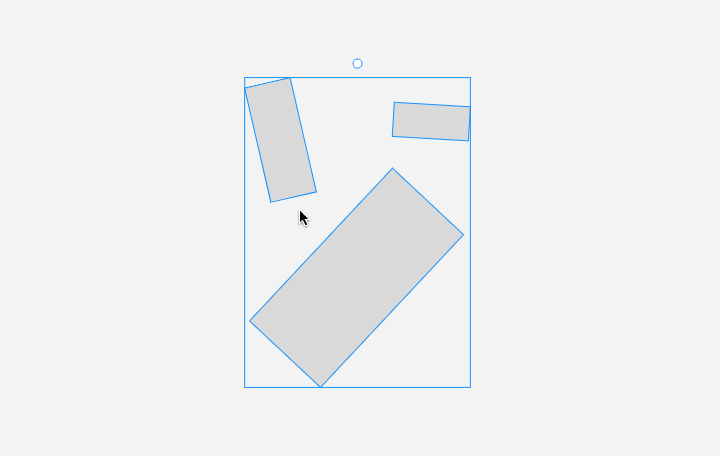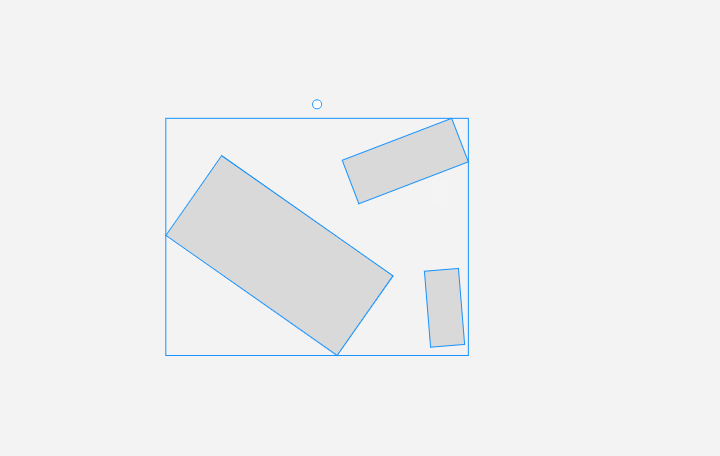
旋轉多個元素

旋轉多個元素則復雜一些。

我們需要改變每個元素的旋轉角度 rotation，以及 x、y 值。

這里我們需要知道一個很重要的信息：元素上所有的點的旋轉結果坐標，都是根據大包圍盒中心旋轉 rotation 得到的。

首先是 rotation，旋轉中心是這個大 bBox 的中心。

我們從元素的中點畫一個向上的向量，這個向量是跟隨著多元素旋轉角度改變的。

所以，和單元素直接賦值不同，多元素旋轉情況下，拖拽中產生的旋轉角度需要作為增量，加在每個旋轉前的元素起始角度上，即：

element.rotation = prevElementRotation + dRotation;

然后是計算每個元素 新的 x 和 y 值。

也很簡單，對旋轉前的中點 cx 和 cy，使用旋轉算法，計算出新的 cx 和 cy ，然后減去寬高/2即可。

需要實現的算法

在這個過程中你需要實現的算法有：

1. 求向量夾角，需要用點積公式。
2. 旋轉算法，需要考慮旋轉中心。
3. 計算 bBox，其實就是將 bBox 轉換為 4 個邊角的坐標，然后取最小的 x、y 和最大的 x、y 重新組合成一個 box。

然后其他就是繁瑣的交互邏輯了。

結尾

至此，我們就實現了元素的旋轉邏輯。晚點我會再出一篇縮放元素的文章。