一起學 WebGL:復合矩陣

大家好,我是前端西瓜哥。之前講了平移矩陣、旋轉矩陣以及縮放矩陣,以及演示了在 WebGL 中的單獨應用的效果。
這次我們看看同時進行多次矩陣變換的組合寫法。
我們將會對一個三角形先平移,然后旋轉。
矩陣乘法
一個坐標(矢量),先進行矩陣變形 1,然后再做矩陣變換 2,它的寫法是:
m2 * m1 * vec第一個矩陣 A 的列數如果等于第二個矩陣 B 的行數,那這兩個矩陣可以做乘法。
矩陣乘法不滿足交換律,即 AxB 通常不等于 BxA。
矩陣乘法,一種理解方式是:A 的第 i 行的每個元素,依次乘以 B 的第 j 列的對應元素,然后加起來,作為新矩陣的第 [i][j] 個元素。
矩陣乘法的計算順序為從左往右。
以一個比較低維度的 2x2 矩陣為例:
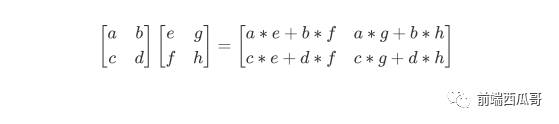
矩陣乘法滿足交換律。
m2 * m1 * vec
= m2 * (m1 * vec)
= (m2 * m1) * vec所以,一個頂點要做多次矩陣變換,我們可以先計算這些矩陣的結果,得到一個復合矩陣,然后再乘以頂點。
當多個頂點做的矩陣變換是一樣的時候,我們就能減少計算量,一些線性計算就得到結果。
這種將一個模型丟到世界坐標系中進行各種變換,我們也稱為 模型變換(model transform)。
頂點著色器中運算
頂點著色器代碼:
const vertexShaderSrc = `
attribute vec4 a_Position;
uniform mat4 u_translateMatrix;
uniform mat4 u_rotateMatrix;
mat4 compoundMatrix = u_rotateMatrix * u_translateMatrix;
void main() {
gl_Position = compoundMatrix * a_Position;
}
`;聲明了兩個 uniform 類型的矩陣 u_translateMatrix 和 u_rotateMatrix,分別保存平移矩陣和旋轉矩陣,然后將它們相乘。
compoundMatrix 因為不需要外部傳入值,所以不需要加 uniform 聲明。
因為是先平移再旋轉,所以平移矩陣在右,旋轉矩陣在左。
平移矩陣的構造:
/****** (1) 平移矩陣 ****/
const dx = 0.5; // 向右移動
const dy = 0; // 向下移動
// z 先不管,沒用到透視矩陣,設置值也看不到效果
const translateMatrix = new Float32Array([
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
dx, dy, 0, 1
]);
// 傳入頂點著色器
const u_translateMatrix = gl.getUniformLocation(
gl.program,
"u_translateMatrix"
);
gl.uniformMatrix4fv(u_translateMatrix, false, translateMatrix);旋轉矩陣的構造:
/****** (2) 旋轉矩陣 ****/
const angle = 60;
const radian = (angle * Math.PI) / 180;
const cos = Math.cos(radian);
const sin = Math.sin(radian);
// prettier-ignore
const rotateMatrix = new Float32Array([
cos, sin, 0, 0,
-sin, cos, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]);
const u_rotateMatrix = gl.getUniformLocation(gl.program, "u_rotateMatrix");
gl.uniformMatrix4fv(u_rotateMatrix, false, rotateMatrix);demo 地址:
https://codesandbox.io/s/eg66e2?file=/index.js。
渲染結果:

使用 JavaScript 運算
換成用 JavaScript 來做矩陣乘法,將計算好的矩陣傳入到著色器中。
頂點著色器只要聲明一個 uniform 類型的 u_compoundMatrix 就好。
uniform 是一個不變的類型,使用下一頂點時還會使用原來的值。如果頂點更換時,值會變,你應該使用的是 attribute 類型。
const vertexShaderSrc = `
attribute vec4 a_Position;
uniform mat4 u_compoundMatrix;
void main() {
gl_Position = u_compoundMatrix * a_Position;
}
`;創建完兩個 Float32Array 的數組后,我們用自己實現的 JavaScript 將它們相乘。
/*************** 計算復合矩陣 *************/
// 兩個 4x4 矩陣相乘的方法。m1 x m2
function multiply(m1, m2) {
const size = 4;
const m = new Float32Array(size * size);
for (let i = 0; i < size; i++) {
for (let j = 0; j < size; j++) {
let sum = 0;
for (let k = 0; k < size; k++) {
sum += m2[i * size + k] * m1[k * size + j];
}
m[i * size + j] = sum;
}
}
return m;
}
// 這里創建了倆 Float32Array 數組
// ...
// 兩個矩陣相乘,得到復合變換矩陣
const xformMatrix = multiply(rotateMatrix, translateMatrix);
// 將計算出來的矩陣傳給著色器
const u_compoundMatrix = gl.getUniformLocation(gl.program, "u_compoundMatrix");
gl.uniformMatrix4fv(u_compoundMatrix, false, xformMatrix);在實現 multiply 方法過程中,有一個容易踩的坑,就是 WebGL 中的矩陣是 按列主序 的,即 m[0] 到 m[1] 對應的是第一列,而不是第一行,我們實現 JavaScript 矩陣乘法的時候要注意,否則就會從 AxB 變成了 BxA。
西瓜哥我就踩了這個坑,發現 JavaScript 實現和預期不符,居然是先旋轉再移動,大眼瞪了半天才發現自己把左邊矩陣的列當成行去運算了。
demo 地址:
https://codesandbox.io/s/hw8wfi?file=/index.js。
渲染效果和在頂點著色器計算的一樣:

如果我們將兩個變換矩陣的順序交換一下,就會得到一個先旋轉再移動的效果。感興趣的朋友可以去線上 demo 修改試試。

結尾
我是前端西瓜哥,歡迎關注我,學習更多前端知識。
頂點的變換可以用矩陣乘法來表示,乘以一個矩陣就是一個變形(比如平移、旋轉、縮放)。如果應用了多個矩陣,我們可以利用矩陣乘法的結合律將這幾個矩陣先預先計算好。
另外一個坑,就是矩陣是用一維數組表示的,且為比較別扭的按列主序,聲明的數組在形式上和矩形真正的樣子有一點不同,需要沿著從左上到右下的軸線進行一個翻轉才行。












































