KNN中不同距離度量對比和介紹
k近鄰算法KNN是一種簡單而強大的算法,可用于分類和回歸任務。他實現簡單,主要依賴不同的距離度量來判斷向量間的區別,但是有很多距離度量可以使用,所以本文演示了KNN與三種不同距離度量(Euclidean、Minkowski和Manhattan)的使用。
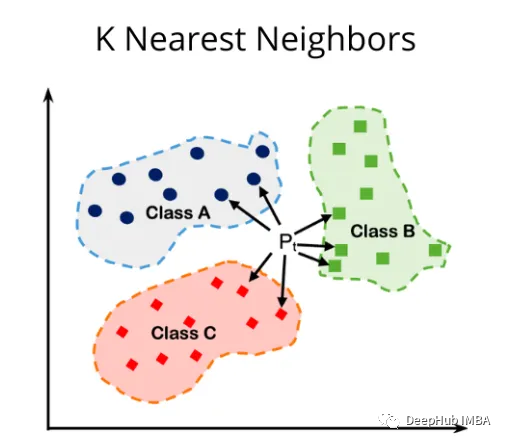
KNN算法概述
KNN是一種惰性、基于實例的算法。它的工作原理是將新樣本的特征與數據集中現有樣本的特征進行比較。然后算法選擇最接近的k個樣本,其中k是用戶定義的參數。新樣本的輸出是基于“k”最近樣本的多數類(用于分類)或平均值(用于回歸)確定的。
有很多距離度量的算法,我們這里選取3個最常用度量的算法來進行演示:
1、歐氏距離 Euclidean Distance
def euclidean_distance(x1, x2):
return math.sqrt(np.sum((x1 - x2)**2))euclidean_distance函數計算多維空間中兩點(x1和x2)之間的歐氏距離,函數的工作原理如下:
- 從x1元素中減去x2,得到對應坐標之間的差值。
- 使用**2運算將差值平方。
- 使用np.sum()對差的平方求和。
- 使用math.sqrt()取總和的平方根。
歐幾里得距離是歐幾里得空間中兩點之間的直線距離。通過計算歐幾里得距離,可以識別給定樣本的最近鄰居,并根據鄰居的多數類(用于分類)或平均值(用于回歸)進行預測。在處理連續的實值特征時,使用歐幾里得距離很有幫助,因為它提供了一種直觀的相似性度量。
2、曼哈頓距離 Manhattan Distance
兩點坐標的絕對差值之和。
def manhattan_distance(x1, x2):
return np.sum(np.abs(x1 - x2))Manhattan _distance函數計算多維空間中兩點(x1和x2)之間的曼哈頓距離,函數的工作原理如下:
- 用np計算x1和x2對應坐標的絕對差值。Abs (x1 - x2)
- 使用np.sum()對絕對差進行求和。
曼哈頓距離,也稱為L1距離或出租車距離,是兩點坐標的絕對差值之和。它代表了當運動被限制為網格狀結構時,點之間的最短路徑,類似于在城市街道上行駛的出租車。
在數據特征具有不同尺度的情況下,或者當問題域的網格狀結構使其成為更合適的相似性度量時,使用曼哈頓距離可能會有所幫助。曼哈頓距離可以根據樣本的特征來衡量樣本之間的相似性或差異性。
與歐幾里得距離相比,曼哈頓距離對異常值的敏感性較低,因為它沒有對差異進行平方。這可以使它更適合于某些數據集或異常值的存在可能對模型的性能產生重大影響的問題。
3、閔可夫斯基距離 Minkowski Distance
它是歐幾里得距離和曼哈頓距離的一般化的表現形式,使用p進行參數化。當p=2時,它變成歐氏距離,當p=1時,它變成曼哈頓距離。
def minkowski_distance(x1, x2, p):
return np.power(np.sum(np.power(np.abs(x1 - x2), p)), 1/p)minkowski_distance函數計算多維空間中兩點(x1和x2)之間的閔可夫斯基距離。
當你想要控制單個特征的差異對整體距離的影響時,使用閔可夫斯基距離會很有幫助。通過改變p值,可以調整距離度量對特征值或大或小差異的靈敏度,使其更適合特定的問題域或數據集。
閔可夫斯基距離可以根據樣本的特征來衡量樣本之間的相似性或不相似性。該算法通過計算適當p值的閔可夫斯基距離,識別出給定樣本的最近鄰居,并根據鄰居的多數類(用于分類)或平均值(用于回歸)進行預測。
KNN 算法的代碼實現
因為KNN算法的原理很簡單,所以我們這里直接使用Python實現,這樣也可以對算法有一個更好的理解:
def knn_euclidean_distance(X_train, y_train, X_test, k):
# List to store the predicted labels for the test set
y_pred = []
# Iterate over each point in the test set
for i in range(len(X_test)):
distances = []
# Iterate over each point in the training set
for j in range(len(X_train)):
# Calculate the distance between the two points using the Euclidean distance metric
dist = euclidean_distance(X_test[i], X_train[j])
distances.append((dist, y_train[j]))
# Sort the distances list by distance (ascending order)
distances.sort()
# Get the k nearest neighbors
neighbors = distances[:k]
# Count the votes for each class
counts = {}
for neighbor in neighbors:
label = neighbor[1]
if label in counts:
counts[label] += 1
else:
counts[label] = 1
# Get the class with the most votes
max_count = max(counts, key=counts.get)
y_pred.append(max_count)
return y_pred這個' knn_euclidean_distance '函數對于解決分類問題很有用,因為它可以根據' k '個最近鄰居中的大多數類進行預測。該函數使用歐幾里得距離作為相似性度量,可以識別測試集中每個數據點的最近鄰居,并相應地預測它們的標簽。我們實現的代碼提供了一種顯式的方法來計算距離、選擇鄰居,并根據鄰居的投票做出預測。
在使用曼哈頓距離時,KNN算法與歐氏距離保持一致,只需要將距離計算函數euclidean_distance修改為manhattan_distance。而閔可夫斯基距離則需要多加一個參數p,實現代碼如下:
def knn_minkowski_distance(X_train, y_train, X_test, k, p):
# List to store the predicted labels for the test set
y_pred = []
# Iterate over each point in the test set
for i in range(len(X_test)):
distances = []
# Iterate over each point in the training set
for j in range(len(X_train)):
# Calculate the distance between the two points using the Minkowski distance metric
dist = minkowski_distance(X_test[i], X_train[j], p)
distances.append((dist, y_train[j]))
# Sort the distances list by distance (ascending order)
distances.sort()
# Get the k nearest neighbors
neighbors = distances[:k]
# Count the votes for each class
counts = {}
for neighbor in neighbors:
label = neighbor[1]
if label in counts:
counts[label] += 1
else:
counts[label] = 1
# Get the class with the most votes
max_count = max(counts, key=counts.get)
y_pred.append(max_count)
return y_pred距離度量對比
我使用的數據集是乳腺癌數據集,可以在kaggle上直接下載
這個數據集是機器學習和數據挖掘中廣泛使用的基準數據集,用于二元分類任務。它是由威廉·h·沃爾伯格(William H. Wolberg)博士及其合作者在20世紀90年代從麥迪遜的威斯康星大學醫院收集的。該數據集可通過UCI機器學習存儲庫公開獲取。
Breast Cancer Wisconsin數據集包含569個實例,每個實例有32個屬性。這些屬性是:
ID number:每個樣本的唯一標識符。
Diagnosis:目標變量有兩個可能的值——“M”(惡性)和“B”(良性)。
剩下的是30個從乳腺腫塊的細針抽吸(FNA)的數字化圖像中計算出來的特征。它們描述了圖像中細胞核的特征。對每個細胞核計算每個特征,然后求平均值,得到10個實值特征:
- Radius:從中心到周邊點的平均距離。
- Texture:灰度值的標準偏差。
- Perimeter:細胞核的周長。
- Area:細胞核的面積。
- Smoothness:半徑長度的局部變化。
- Compactness:周長2/面積- 1.0。
- Concavity:輪廓中凹部分的嚴重程度。
- Concave points:輪廓的凹部分的數目。
- Symmetry:細胞核的對稱性。
- Fractal dimension:“Coastline approximation”- 1
對每張圖像計算這十個特征的平均值、標準誤差和最小或最大值(三個最大值的平均值),總共得到30個特征。數據集不包含任何缺失的屬性值。
由于數據集包含30個特征,我們需要對數據集進行特征選擇。這種方法的主要目的是通過選擇與目標變量具有強線性關系的較小的特征子集來降低數據集的維數。通過選擇高相關性的特征,目的是保持模型的預測能力,同時減少使用的特征數量,潛在地提高模型的性能和可解釋性。這里需要注意的是,該方法只考慮特征與目標變量之間的線性關系,如果底層關系是非線性的,或者特征之間存在重要的交互作用,則該方法可能無效。
讀取數據并計算相關系數:
df = pd.read_csv('/kaggle/input/breast-cancer-wisconsin-data/data.csv')
corr = df.corr()
corr_threshold = 0.6
selected_features = corr.index[np.abs(corr['diagnosis']) >= corr_threshold]
new_cancer_data = df[selected_features]訓練代碼:
X_train_np = np.array(X_train)
X_test_np = np.array(X_test)
# Convert y_train and y_test to numpy arrays
y_train_np = np.array(y_train)
y_test_np = np.array(y_test)
k_values = list(range(1, 15))
accuracies = []
for k in k_values:
y_pred = knn_euclidean_distance(X_train_np, y_train_np, X_test_np, k)
accuracy = accuracy_score(y_test_np, y_pred)
accuracies.append(accuracy)
# Create a data frame to store k values and accuracies
results_df = pd.DataFrame({'k': k_values, 'Accuracy': accuracies})
# Create the interactive plot using Plotly
fig = px.line(results_df, x='k', y='Accuracy', title='KNN Accuracy for Different k Values', labels={'k': 'k', 'Accuracy': 'Accuracy'})
fig.show()
# Get the best k value
best_k = k_values[accuracies.index(max(accuracies))]
best_accuracy = max(accuracies)
print("Best k value is:", best_k , "where accuracy is:" ,best_accuracy)上面代碼使用歐幾里得距離將KNN算法應用于分類問題,同時改變鄰居的數量(k)以找到最高精度的最佳k值。它使用訓練集(X_train_np和y_train_np)來訓練模型,使用測試集(X_test_np和y_test_np)來進行預測和評估模型的性能。
k是KNN算法的一個超參數,選擇正確的k值對于實現最佳模型性能至關重要,因為k值太小可能導致過擬合,而k值太大可能導致欠擬合。通過可視化k值與其對應的精度之間的關系,可以深入了解模型的性能,并為問題選擇最合適的k值。
閔可夫斯基距離的代碼修改如下:
# Run the KNN algorithm on the test set for different k and p values
k_values = list(range(1, 15))
p_values = list(range(1, 6))
results = []
for k in k_values:
for p in p_values:
y_pred = knn_minkowski_distance(X_train_np, y_train_np, X_test_np, k, p)
accuracy = accuracy_score(y_test_np, y_pred)
results.append((k, p, accuracy))
# Create a data frame to store k, p values, and accuracies
results_df = pd.DataFrame(results, columns=['k', 'p', 'Accuracy'])
# Create the 3D plot using Plotly
fig = go.Figure(data=[go.Scatter3d(
x=results_df['k'],
y=results_df['p'],
z=results_df['Accuracy'],
mode='markers',
marker=dict(
size=4,
color=results_df['Accuracy'],
colorscale='Viridis',
showscale=True,
opacity=0.8
),
text=[f"k={k}, p={p}, Acc={acc:.2f}" for k, p, acc in results]
)])
fig.update_layout(scene=dict(
xaxis_title='k',
yaxis_title='p',
zaxis_title='Accuracy'
))
fig.show()為了進一步改善我們的結果,我們還可以數據集進行縮放。應用特征縮放的主要目的是確保所有特征具有相同的尺度,這有助于提高基于距離的算法(如KNN)的性能。在KNN算法中,數據點之間的距離對確定它們的相似度起著至關重要的作用。如果特征具有不同的尺度,則算法可能會更加重視尺度較大的特征,從而導致次優預測。通過將特征縮放到均值和單位方差為零,算法可以平等地對待所有特征,從而獲得更好的模型性能。
本文將使用StandardScaler()和MinMaxScaler()來擴展我們的數據集。StandardScaler和MinMaxScaler是機器學習中兩種流行的特征縮放技術。這兩種技術都用于將特征轉換為公共尺度,這有助于提高許多機器學習算法的性能,特別是那些依賴于距離的算法,如KNN或支持向量機(SVM)。
使用不同的尺度和不同的距離函數訓練KNN,可以進行比較并選擇最適合數據集的技術。我們得到了以下結果:
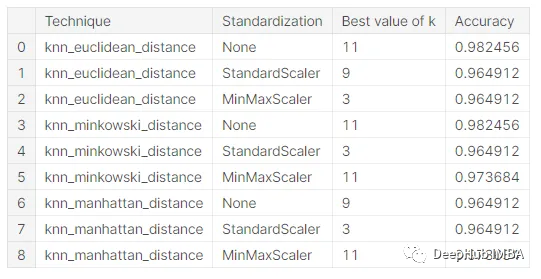
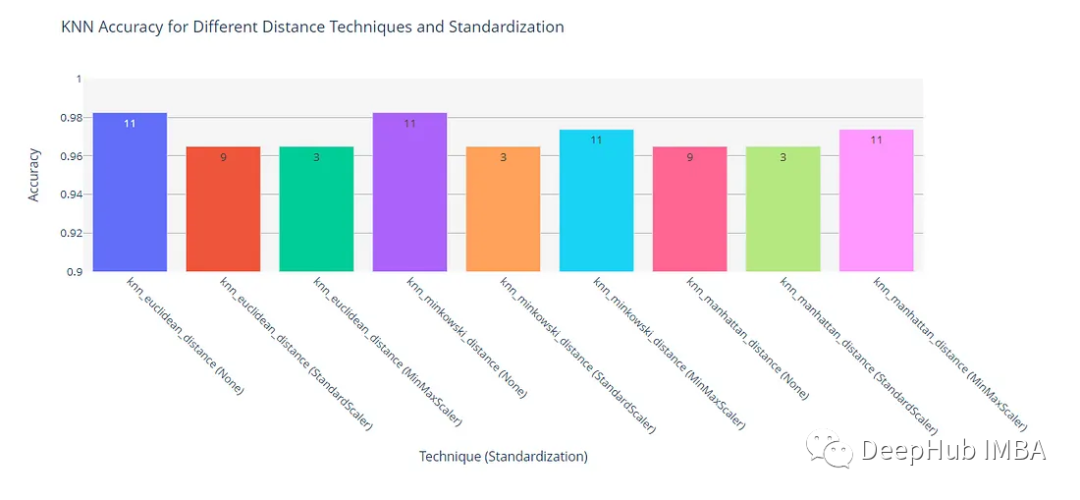
可以使用柱狀圖表示來更好地分析和理解這些結果。
總結
根據上面的結果,我們可以得到以下的結論:
在不進行特征縮放時,歐幾里得距離和閔可夫斯基距離都達到了0.982456的最高精度。
曼哈頓離在所有情況下的精度都比較低,這表明歐幾里得或閔可夫斯基距離可能更適合這個問題。當閔可夫斯基距離度量中的p值為2時,它等于歐幾里得距離。在我們這個實驗中這兩個指標的結果是相同的,也證明了這是正確的。
對于歐幾里得和閔可夫斯基距離度量,不應用任何特征縮放就可以獲得最高的精度。而對于曼哈頓距離,與非縮放數據相比,StandardScaler和MinMaxScaler都提高了模型的性能。這表明特征縮放的影響取決于所使用的距離度量。
最佳k值:最佳k值取決于距離度量和特征縮放技術。例如,k=11是不應用縮放并且使用歐幾里得距離或閔可夫斯基距離時的最佳值,而k=9是使用曼哈頓距離時的最佳值。當應用特征縮放時,最佳k值通常較低,范圍在3到11之間。
最后,該問題的最佳KNN模型使用歐式距離度量,無需任何特征縮放,在k=11個鄰居時達到0.982456的精度。這應該是我們這個數據集在使用KNN時的最佳解。