本文將介紹3個在數據集中查找離群值的Python方法。

離群值（Outliers）是指在數據集中與其他數據點明顯不同或者異常的數據點。這些數據點可能比其他數據點要遠離數據集的中心，或者具有異常的數值。離群值可能是由于數據采集錯誤、異常事件、測量誤差或者其他未知因素引起的。

離群值的存在可以對數據分析和統計建模產生重要影響，因為它們可能導致模型不準確或者產生誤導性的結果。

我們先創建一個演示的數據

import pandas as pd
 import matplotlib.pyplot as plt
 
 name = ['John', 'Victor', 'Carlos', 'Leo', 'Kevin', 'Silva', 'Johnson', 'Lewis', 'George', 'Daniel', 'Harry', 'Jordan', 'James']
 salary = [4000, 1000, 2000, 100000, 3500, 6000, 1500, 3000, 2500, 3600, 2100, 1700, 1600]
 
 df = pd.DataFrame({'Name': name, 'Salary': salary})
 
 plt.boxplot(df['Salary'])
 plt.show()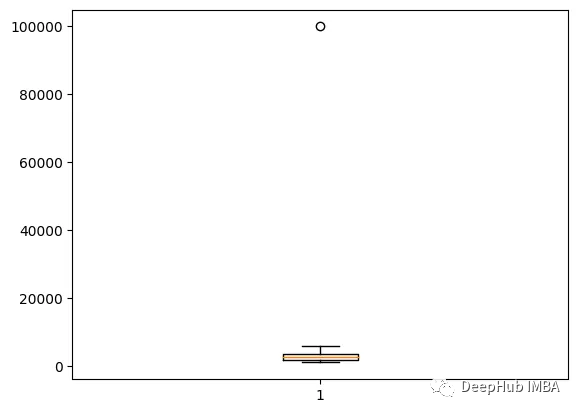

可以看到上面的點就是離群值，下面我們將介紹快速找到它的方法。

四分位極差法

首先找到第一和第三個四分位數值，通常記為Q1和Q3。然后用Q3減去Q1計算四分位差(IQR)。

通過減去/增加1.5倍IQR來計算下界和上界。上下邊界外的值就是離群值

q1 = df['Salary'].quantile(0.25)
 q3 = df['Salary'].quantile(0.75)
 iqr = q3 - q1
 
 lower_bound = q1 - 1.5 * iqr
 upper_bound = q3 + 1.5 * iqr
 
 outliers = df[(df['Salary'] < lower_bound) | (df['Salary'] > upper_bound)]

1.5倍IQR的閾值通常是一種常用的標準，閾值的選擇可以根據具體情況進行調整。有時候，也可以選擇更嚴格或更寬松的閾值，以適應特定的數據分析需求。

標準偏差法

標準偏差法（Standard Deviation Method）使用數據的標準差來判斷數據點是否偏離了數據。上界和下界是均值和3倍標準差的加減。

他的方法如下：

計算平均值和標準偏差： 首先，計算數據的平均值（Mean）和標準偏差（Standard Deviation）。平均值代表了數據的中心位置，標準偏差衡量了數據的分散程度。

確定閾值： 定義一個閾值，通常是標準偏差的倍數（通常為2或3倍標準偏差）。這個閾值決定了什么樣的數據點被認為是離群值。

識別離群值： 計算每個數據點與平均值之間的差值，然后將這個差值與閾值比較。如果差值超過了閾值，數據點被認為是離群值。

mean = df.Salary.mean()
 std = df.Salary.std()
 
 upper_bound = mean + 3 * std
 lower_bound = mean - 3 * std
 
 outliers = df[(df['Salary'] < lower_bound) | (df['Salary'] > upper_bound)]

標準偏差法的優點在于簡單易懂，而且不需要假設數據分布的形狀。但需要注意以下幾點：

• 通常情況下，閾值使用2或3倍標準偏差作為閾值，但這個值可能需要根據具體情況進行調整。
• 這種方法對于正態分布的數據集效果較好，但對于偏斜分布的數據，可能會導致誤判。
• 標準偏差法可能不適用于小樣本，因為標準偏差在小樣本中可能不夠穩定。

Z-分數法

Z-分數（Z-Score）法測量了數據點與數據集平均值之間的偏差，以標準化方式表示這個偏差。對于每個數據點，計算它與平均值之間的差值，然后將這個差值除以標準偏差，得到Z-分數。如果z-score大于3.0或小于-3.0，則該值可歸類為離群值。

我們可以直接使用scipy提供的函數來進行計算

from scipy import stats
 
 df['Salary_zscore'] = stats.zscore(df['Salary'])
 filtered_df = df[(df['Salary_zscore'] <= 3) & (df['Salary_zscore'] >= -3)]

Z-分數法適用于各種類型的數據分布，不需要假設數據分布的形狀。并且提供了標準化的度量，使得不同數據集之間的離群值比較更加容易。

總結

以上是可以快速找到離群值的統計學方法，除此以外，還有一些機器學習的方法例如:

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）： DBSCAN是一種密度聚類算法，也可用于檢測離群值。它根據數據點的密度來識別離群值，將密度較低的點視為離群值。

LOF（Local Outlier Factor）： LOF是一種局部離群值因子方法，用于檢測局部區域內的離群值。它考慮了每個數據點周圍的局部密度與相鄰點的密度之間的比率，從而識別離群值。

Isolation Forest： Isolation Forest是一種基于隨機森林的離群值檢測方法，它通過構建樹結構來識別離群值。由于使用了隨機性，它對高維數據和大數據集非常有效。

但是這些方法執行的速度會很慢，如果對于速度要求比較嚴格還是需要謹慎選擇。