深入了解桶排序:原理、性能分析與 Java 實現
作者:修己xj
桶排序是一種簡單但有效的排序算法,特別適用于某些特定范圍內數據的排序,當數據分布均勻時,性能較好。然而,對于不均勻分布的數據,其性能可能下降,因此在實際應用中需要謹慎選擇。
桶排序(Bucket Sort)是一種排序算法,通常用于將一組數據分割成有限數量的桶(或容器),然后對每個桶中的數據進行排序,最后將這些桶按順序合并以得到排好序的數據集。
 圖片
圖片
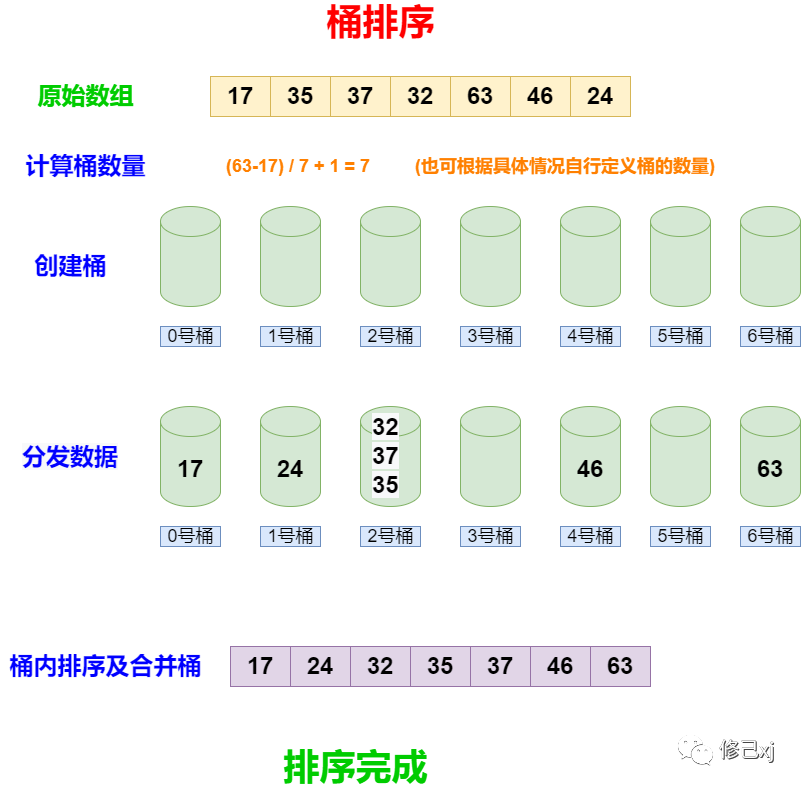
桶排序原理
- 確定桶的數量:首先,確定要使用的桶的數量。通常,桶的數量可以根據數據范圍和分布情況來確定。
- 分發數據:將待排序的元素按照一定的規則(例如,數值大小)分發到不同的桶中。
- 每個桶內排序:對每個桶內的元素進行排序。這可以使用任何排序算法,例如插入排序或快速排序。
- 合并桶:將每個桶內的元素按照桶的順序合并,形成有序序列。
圖示如下:
 圖片
圖片
桶排序性能分析
- 時間復雜度:桶排序的時間復雜度取決于數據的分布情況。在最理想的情況下,當數據均勻分布在各個桶中時,每個桶內的排序時間復雜度是 ,因此總體時間復雜度為 。但在最壞情況下,如果所有數據都分布在一個桶中,桶內排序的時間復雜度可以達到 。在平均情況下,桶排序通常表現為 。
- 空間復雜度:桶排序需要額外的存儲空間來存儲桶,因此空間復雜度為 ,其中 n 表示排序元素的個數,k 表示桶的數量。
- 穩定性:桶排序通常是穩定的,即相等元素的相對順序在排序后不會發生變化。
使用場景
桶排序適用于以下情況:
- 數據分布相對均勻。
- 數據范圍已知,可以將數據映射到有限數量的桶中。
Java 代碼實現
以下是使用 Java 實現桶排序的示例代碼,其中每個桶中的元素排序使用的是快速排序,快速排序的詳解請參考歷史博文 深入了解快速排序:原理、性能分析與 Java 實現:
public class Test {
public static void main(String[] args) {
int[] arr = new int[]{17,35,37,32,63,46,24};
System.out.println("原始數組:"+ Arrays.toString(arr));
bucketSort(arr);
System.out.println("排序后的數組:"+ Arrays.toString(arr));
}
//桶排序
public static void bucketSort(int[] arr){
int maxVal = Arrays.stream(arr).max().getAsInt();
int minVal = Arrays.stream(arr).min().getAsInt();
//計算桶的數量,+1 是保證至少有1個桶來裝數據
int bucketCount = (maxVal - minVal)/arr.length + 1;
// 用于存儲每個桶中元素的出現次數
int[] order = new int[bucketCount];
// 用于存儲每個桶中的數據
int[][] output = new int[bucketCount][arr.length];
int len = arr.length;
//每個桶中數據的范圍,+1 是至少每個桶中的數據范圍為1
int rang = (maxVal - minVal)/bucketCount +1;
//將待排序的數組中的所有元素放入到桶中
for(int i = 0; i < len; i++ ){
//計算數組元素所在的桶
int index = (arr[i] - minVal) / rang ;
//將元素放入指定的桶
output[index][order[index]] = arr[i];
//添加桶元素的計數
order[index]++;
}
System.out.println("桶計數數組為:"+ Arrays.toString(order));
int k = 0;
//遍歷桶,將桶中的元素放入源數組中,并對其進行快速排序
for(int i = 0; i < bucketCount; i++){
int j ;
if(order[i] > 0){
// 將桶中的元素放入源數組中
for(j = 0; j < order[i]; j++){
arr[k++] = output[i][j];
}
//對桶中的元素進行快速排序
quickSort(arr,k-j,k-1);
}
}
}
//快速排序的詳解請參考歷史博文 `深入了解快速排序:原理、性能分析與 Java 實現`
public static void quickSort(int[] arr,int left,int right) {
//遞歸結束條件left < right
if(left < right){
// 通過分區函數得到基準元素的索引
int pivotIndex = partition(arr, left, right);
//遞歸對基準元素左邊的子數組進行快速排序
quickSort(arr,left,pivotIndex-1);
//遞歸對基準元素右邊的子數組進行快速排序
quickSort(arr,pivotIndex+1,right);
}
}
public static int partition(int[] arr,int left,int right) {
// 選擇最后一個元素作為基準元素
int pivot = arr[right];
int i = left;
//循環數組,如果滿足條件,則將滿足條件的元素交換到arr[i],同時i++,循環完成之后i之前的元素則全部為小于基準元素的元素
for (int j = left; j < right; j++) {
if(arr[j] < pivot){
if(j != i){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
i++;
}
}
// 交換 arr[i] 和基準元素
int temp = arr[i];
arr[i] = arr[right];
arr[right] = temp;
//返回基準元素的下標
return i;
}
}輸出結果為:
原始數組:[17, 35, 37, 32, 63, 46, 24]
桶計數數組為:[1, 1, 3, 0, 1, 0, 1]
排序后的數組:[17, 24, 32, 35, 37, 46, 63]這是一個基本的桶排序實現示例。您可以根據實際需求和數據類型進行擴展和優化。
總結
總的來說,桶排序是一種簡單但有效的排序算法,特別適用于某些特定范圍內數據的排序,當數據分布均勻時,性能較好。然而,對于不均勻分布的數據,其性能可能下降,因此在實際應用中需要謹慎選擇。
責任編輯:武曉燕
來源:
修己xj