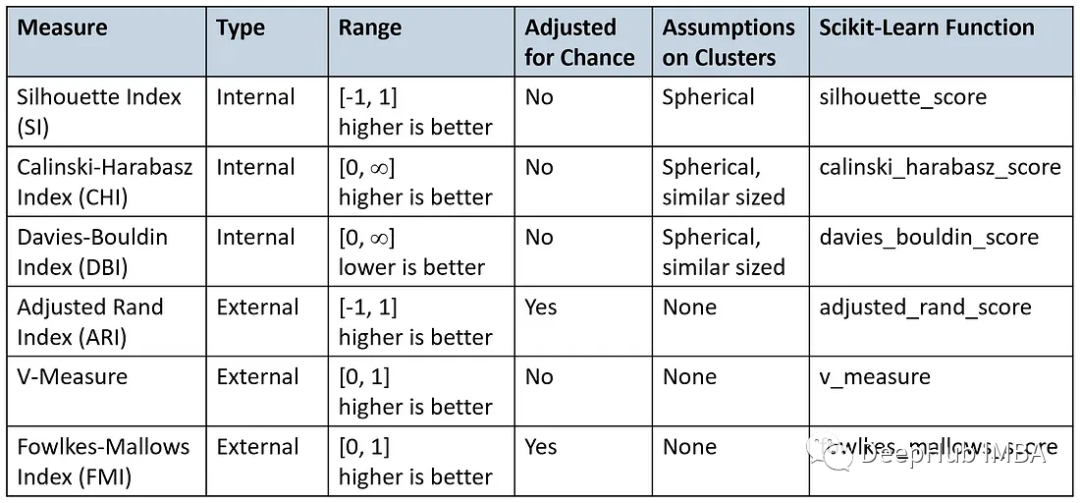
六個常用的聚類評價指標
評估聚類結果的有效性,即聚類評估或驗證,對于聚類應用程序的成功至關重要。它可以確保聚類算法在數據中識別出有意義的聚類,還可以用來確定哪種聚類算法最適合特定的數據集和任務,并調優這些算法的超參數(例如k-means中的聚類數量,或DBSCAN中的密度參數)。
雖然監督學習技術有明確的性能指標,如準確性、精度和召回率,但評估聚類算法更具挑戰性:
由于聚類是一種無監督學習方法,因此沒有可以比較聚類結果的基礎真值標簽。
確定“正確”簇數量或“最佳”簇通常是一個主觀的決定,即使對領域專家也是如此。一個人認為是有意義的簇,另一個人可能會認為是巧合。
在許多真實世界的數據集中,簇之間的界限并不明確。一些數據點可能位于兩個簇的邊界,可以合理地分配給兩個簇。
不同的應用程序可能優先考慮簇的不同方面。例如,在一個應用程序中,可能必須有緊密、分離良好的簇,而在另一個應用程序中,捕獲整體數據結構可能更重要。
考慮到這些挑戰,通常建議結合使用評估指標、視覺檢查和領域專業知識來評估簇性能。
一般來說,我們使用兩種類型的聚類評估度量(或度量):
內部:不需要任何基礎事實來評估簇的質量。它們完全基于數據和聚類結果。
外部:將聚類結果與真值標簽進行比較。(因為真值標簽在數據中是沒有的,所以需要從外部引入)
通常,在實際的應用程序中,外部信息(如真值標簽)是不可用的,這使得內部度量成為簇驗證的唯一可行選擇。
在本文中,我們將探討聚類算法的各種評估指標,何時使用它們,以及如何使用Scikit-Learn計算它們。
內部指標
由于聚類的目標是使同一簇中的對象相似,而不同簇中的對象不同,因此大多數內部驗證都基于以下兩個標準:
緊湊性度量:同一簇中對象的緊密程度。緊湊性可以用不同的方法來衡量,比如使用每個簇內點的方差,或者計算它們之間的平均成對距離。
分離度量:一個簇與其他簇的區別或分離程度。分離度量的例子包括簇中心之間的成對距離或不同簇中對象之間的成對最小距離。
我們將描述三種最常用的內部度量方法,并討論它們的優缺點。
1、輪廓系數
輪廓系數(或分數)通過比較每個對象與自己的聚類的相似性與與其他聚類中的對象的相似性來衡量聚類之間的分離程度[1]。
我們首先定義數據點x的輪廓系數為:
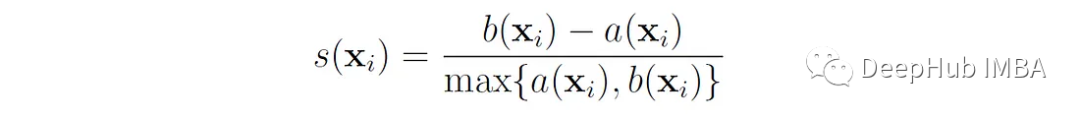
這里的A (x′)是x′到簇中所有其他數據點的平均距離。或者說 如果點x∈屬于簇C∈,那么
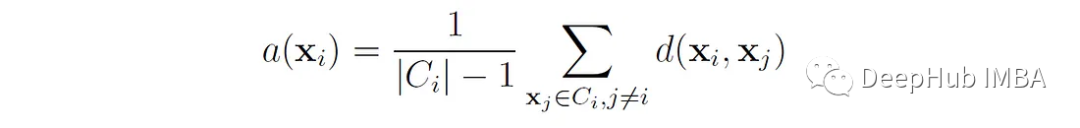
其中d(x, x?)是點x和x之間的距離?。我們可以將a(x ^ e)解釋為點x ^ e與其自身簇匹配程度的度量(值越小,匹配越好)。對于大小為1的簇,a(x′f)沒有明確定義,在這種情況下,我們設s(x′f) = 0。
B (x′)是x′與相鄰簇中點之間的平均距離,即點到x′的平均距離最小的簇:
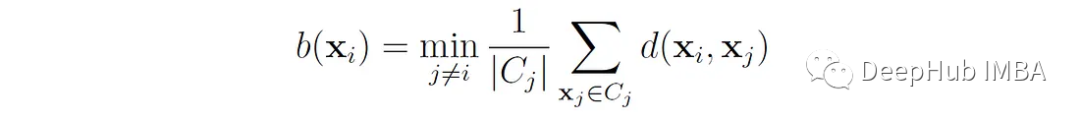
輪廓系數的取值范圍為-1到+1,值越高表示該點與自己的聚類匹配得越好,與鄰近的聚類匹配得越差。
基于樣本的輪廓系數,我們現在將輪廓指數(SI)定義為所有數據點上系數的平均值:
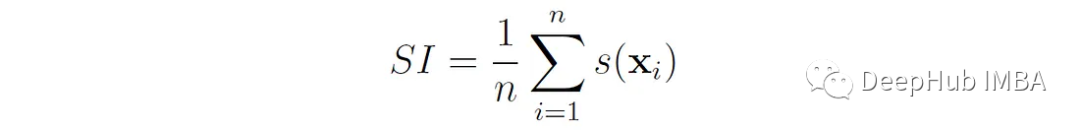
這里的n為數據點總數。
輪廓系數提供了對聚類質量的整體衡量:
接近1意味著緊湊且分離良好。
在0附近表示重疊。
接近-1表示簇的簇太多或太少。
sklearn的Metrics提供了許多聚類評估指標,為了演示這些指標的使用,我們將創建一個合成數據集,并使用不同的k值對其應用k-means聚類。然后,我們將使用評估指標來比較這些聚類的結果。
首先使用make_blobs()函數從3個正態分布的聚類中隨機選擇500個點生成一個數據集,然后對其進行歸一化,以確保特征具有相同的尺度:
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
X, y = make_blobs(n_samples=500, centers=3, cluster_std=0.6, random_state=0)
X = StandardScaler().fit_transform(X)讓我們來繪制數據集:
def plot_data(X):
sns.scatterplot(x=X[:, 0], y=X[:, 1], edgecolor='k', legend=False)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plot_data(X)
然后在k = 2,3,4運行k-means聚類,并將聚類結果存儲在三個不同的變量中:
from sklearn.cluster import KMeans
labels_k2 = KMeans(n_clusters=2, random_state=0).fit_predict(X)
labels_k3 = KMeans(n_clusters=3, random_state=0).fit_predict(X)
labels_k4 = KMeans(n_clusters=4, random_state=0).fit_predict(X)現可以使用函數sklearn.metrics.silhouette_score()來計算每輪廓分數。
from sklearn.metrics import silhouette_score
print(f'SI(2 clusters): {silhouette_score(X, labels_k2):.3f}')
print(f'SI(3 clusters): {silhouette_score(X, labels_k3):.3f}')
print(f'SI(4 clusters): {silhouette_score(X, labels_k4):.3f}')結果如下:
SI(2 clusters): 0.569
SI(3 clusters): 0.659
SI(4 clusters): 0.539可以看到當k = 3時,得分最高,并且低于1,這表明簇之間沒有完全分離。
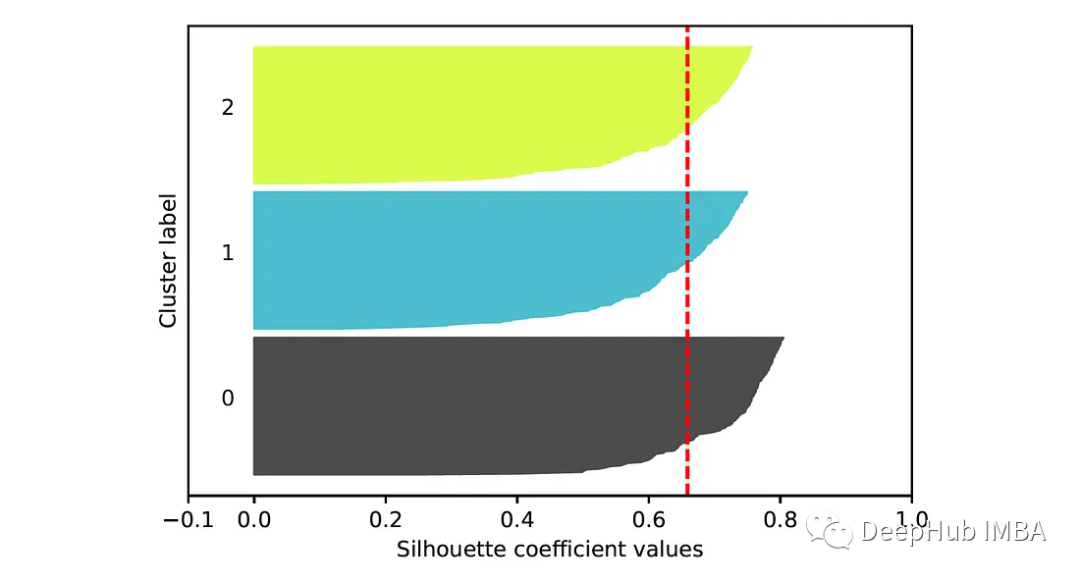
為了計算每個樣本的輪廓系數,我們可以使用函數sklearn.metrics.silhouette_samples。基于這些系數,可以建立一個輪廓圖,它提供了一種評估每個對象在其簇中的位置的方法。在這張圖中,每個點的輪廓系數用一條水平線表示(更長的條形表示更好的聚類)。這些條按簇排列和分組。每個聚類部分的高度表示該聚類中的點的數量。
import matplotlib.cm as cm
from sklearn.metrics import silhouette_samples
def silhouette_plot(X, cluster_labels):
n_clusters = len(np.unique(cluster_labels))
silhouette_avg = silhouette_score(X, cluster_labels)
# Compute the silhouette coefficient for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Get the silhouette coefficients for samples in cluster i and sort them
cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
cluster_silhouette_values.sort()
# Compute the height of the cluster section
cluster_size = len(cluster_silhouette_values)
y_upper = y_lower + cluster_size
# Plot the coefficients for cluster i using horizontal bars
color = cm.nipy_spectral(float(i) / n_clusters)
plt.fill_betweenx(np.arange(y_lower, y_upper), 0, cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Show the cluster numbers at the middle
plt.text(-0.05, y_lower + 0.5 * cluster_size, str(i))
# Compute the new y_lower for the next cluster
y_lower = y_upper + 10
# Draw a vertical line for the average silhouette score
plt.axvline(x=silhouette_avg, color='red', linestyle='--')
plt.yticks([]) # Clear the yaxis labels / ticks
plt.xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
plt.xlabel('Silhouette coefficient values')
plt.ylabel('Cluster label')k = 3的k-means聚類輪廓圖為:
k = 4:
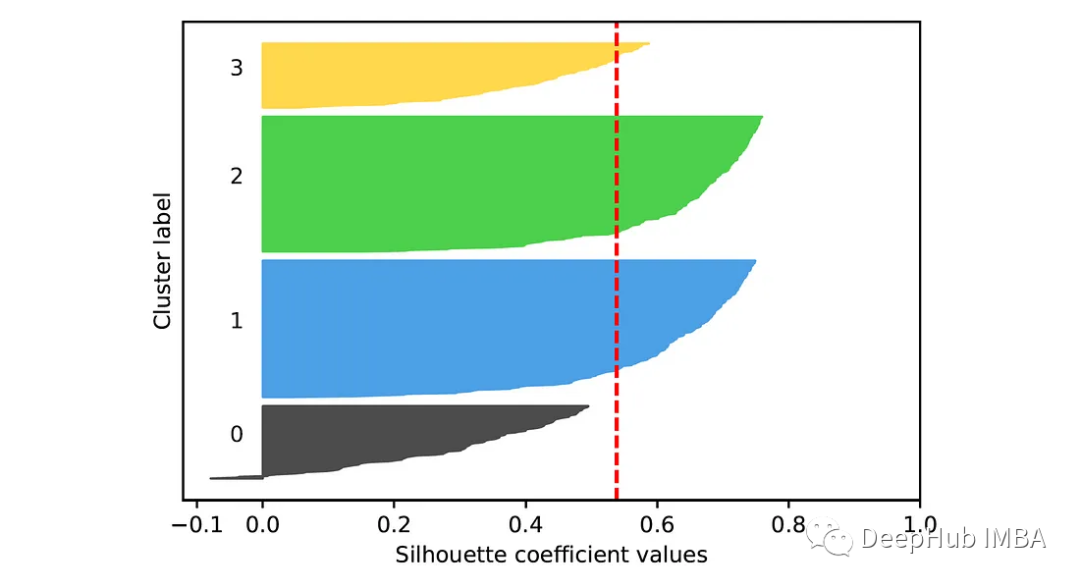
在第二張圖中,我們可以看到類0和類3中的大多數點的輪廓分數低于平均分數。這表明這些聚類可能不代表數據集中的自然分組。
讓我們總結一下輪廓分數的利弊。
優點:
- 很容易解讀。它的取值范圍是-1到1,接近1的值表示分離良好的簇,接近-1的值表示聚類較差。
- 它不僅提供了對整體簇質量的洞察,還提供了對單個簇質量的洞察。這通常使用一個輪廓圖來可視化,它顯示了簇中的每個點對總體得分的貢獻。
- 它可以通過比較不同k值的分數并取最大值來確定k-means等算法中的最優簇數。這種方法往往比肘部法更精確,因為肘部法往往需要主觀判斷。
缺點:
- 傾向于支持凸簇,而非凸或不規則形狀的簇可能表現不佳。
- 不考慮簇的密度,這對于評估基于密度的算法(如DBSCAN)很重要。
- 當簇之間存在重疊時,輪廓評分可能提供模糊的結果。
- 可能難以識別較大簇中的子簇。
- 計算量很大,因為它需要計算所有O(n2)個點之間的成對距離。這可能會使評估過程比聚類本身更昂貴(例如,當使用k-means時)。
- 對噪聲和異常值敏感,因為它依賴于可能受異常值影響的最小成對距離。
2、方差比準則(Calinski-Harabasz Index)
由于Calinski-Harabasz指數的本質是簇間距離與簇內距離的比值,且整體計算過程與方差計算方式類似,所以又將其稱之為方差比準則。
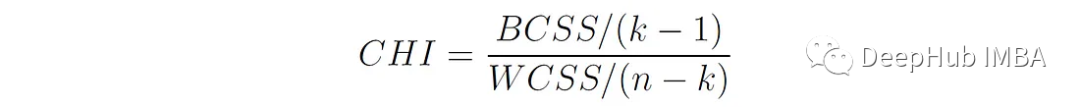
K是簇的數量,N是數據點的總數BCSS (between - cluster Sum of Squares)是每個聚類質心(mean)與整體數據質心(mean)之間歐氏距離的加權平方和:
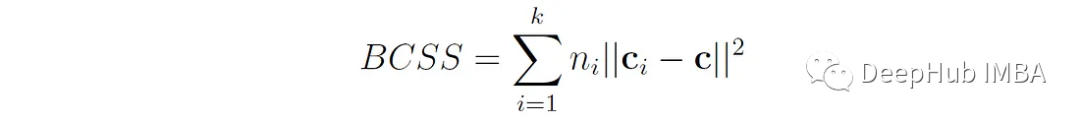
其中n′′是簇i中數據點的個數,c′′是簇i的質心(均值),c是所有數據點的總體質心(均值)。BCSS衡量簇之間的分離程度(越高越好)。
WCSS (Within-Cluster Sum of Squares)是數據點與其各自的聚類質心之間的歐氏距離的平方和:
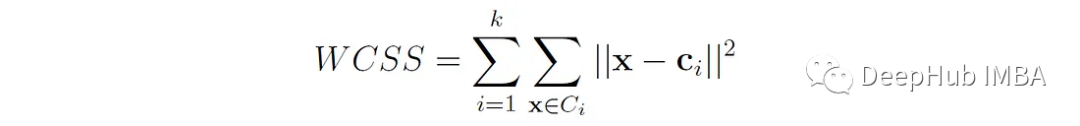
WCSS度量簇的緊湊性或內聚性(越小越好)。最小化WCSS(也稱為慣性)是基于質心的聚類(如k-means)的目標。
CHI的分子表示由其自由度k - 1歸一化的簇間分離(固定k - 1個簇的質心也決定了第k個質心,因為它的值使所有質心的加權和與整個數據質心匹配)。CHI的分母表示由其自由度n- k歸一化的簇內離散度(固定每個簇的質心會使每個簇的自由度減少1)。
將BCSS和WCSS按其自由度劃分有助于使值規范化,使它們在不同數量的簇之間具有可比性。如果沒有這種歸一化,CH指數可能會因k值較高而被人為夸大,從而很難確定指標值的增加是由于真正更好的聚類還是僅僅由于簇數量的增加。
CHI值越高,表示聚類效果越好,因為這意味著數據點在聚類之間的分布比在聚類內部的分布更分散。
在Scikit-Learn中,我們可以使用函數sklearn.metrics.calinski_harabasz_score()來計算這個值。
from sklearn.metrics import calinski_harabasz_score
print(f'CH(2 clusters): {calinski_harabasz_score(X, labels_k2):.3f}')
print(f'CH(3 clusters): {calinski_harabasz_score(X, labels_k3):.3f}')
print(f'CH(4 clusters): {calinski_harabasz_score(X, labels_k4):.3f}')結果如下:
CH(2 clusters): 734.120
CH(3 clusters): 1545.857
CH(4 clusters): 1212.066當k = 3時,CHI得分最高,這也跟上面的輪廓系數得到的結果一樣。
Calinski-Harabasz指數的優缺點如下:
優點:
- 計算簡單,計算效率高。
- 很容易理解。數值越高通常表示聚類效果越好。
- 像輪廓系數一樣,它可以用來找到最優的簇數。
- 有一定的理論依據(它類似于單變量分析中的f檢驗統計量,它比較組間方差和組內方差)。
缺點:
- 傾向于支持凸簇,對于不規則形狀的簇可能表現不佳。
- 可能在不同大小的簇中表現不佳,因為大型簇內的方差會不成比例地影響BCSS和WCSS之間的平衡。
- 不適合評估像DBSCAN這樣基于密度的簇。
- 對噪聲和異常值敏感,因為這些會顯著影響簇內和簇間的分散。
3、Davies-Bouldin指數(DB值)
戴維斯-博爾丁指數(Davies-Bouldin index, DBI)[3]衡量每個聚類與其最相似的聚類之間的平均相似度,其中相似度定義為聚類內距離(聚類中點到聚類中心的距離)與聚類間距離(聚類中心之間的距離)之比。
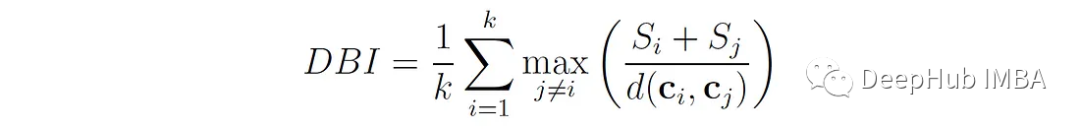
S ? 是簇i中所有點到簇c ? 質心的平均距離
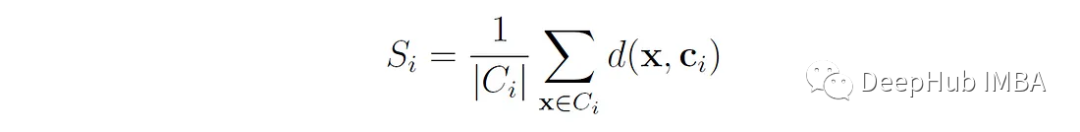
S?衡量簇的“擴散”或“大小”。D (c?,c?)是簇I和j的質心之間的距離。
比值(S?+ S?)/ d(c?,c?)表示聚類i和聚類j之間的相似度,即聚類之間的距離和重疊程度。當兩個簇都“大”(即具有較大的內部距離)時,分子(即兩個簇的擴散之和)就很高。當簇彼此靠近時,表示簇質心之間距離的分母較低。因此,如果分子和分母之間的比例較大,則兩個簇可能重疊或分離不好。相反如果比例很小,則表明簇相對于它們的大小是分開的。
對于每一個聚類i,DB值確定最大這個比率的聚類j,即與聚類i最相似的聚類。最終的DB值是所有聚類的這些最壞情況相似度的平均值。
因此,DB值越低,表明簇越緊湊且分離良好,其中0是可能的最低值。
在Scikit-Learn中可以使用函數sklearn.metrics.davies_bouldin_score()來計算。
from sklearn.metrics import davies_bouldin_score
print(f'BD(2 clusters): {davies_bouldin_score(X, labels_k2):.3f}')
print(f'BD(3 clusters): {davies_bouldin_score(X, labels_k3):.3f}')
print(f'BD(4 clusters): {davies_bouldin_score(X, labels_k4):.3f}')結果如下:
BD(2 clusters): 0.633
BD(3 clusters): 0.480
BD(4 clusters): 0.800當k = 3時,DBI得分最低。
優點:
- 易于快速計算。
- 很容易理解。該數值越小表示聚類越好,值為0表示聚類比較理想。
- 和前兩個分數一樣,它可以用來找到最優的簇數。
缺點:
- 傾向于支持凸簇,對于不同大小或不規則形狀的簇可能表現不佳。
- 對于評估基于密度的聚類算法(如DBSCAN)效率較低。
- 噪聲和異常值會顯著影響指數。
其他內部指標
還有許多其他內部聚類評價方法。參見[2],詳細研究了11種內部度量(包括上面提到的那些)及其在驗證不同類型數據集聚類方面的有效性。
外部指標
當數據點的真實標簽已知時,則可以使用外部評價指標。這些度量將聚類算法的結果與真值標簽進行比較。
1、列聯矩陣(contingency matrix)
與分類問題中的混淆矩陣類似,列聯矩陣(或表)描述了基本真值標簽和聚類標簽之間的關系。
矩陣的行表示真類,列表示簇。矩陣中的每個單元格,用n∈?表示,包含了類標號為i并分配給聚類j的數據點的個數。
我們可以通過sklearn.metrics.cluster.contingency_matrix()構建列聯矩陣。該函數以真值標簽和聚類標簽作為參數進行評估。
from sklearn.metrics.cluster import contingency_matrix
true_labels = [0, 0, 0, 1, 1, 1]
cluster_labels = [0, 0, 1, 1, 2, 2]
contingency_matrix(true_labels, cluster_labels)結果如下:
array([[2, 1, 0],
[0, 1, 2]], dtype=int64)矩陣表示將兩個0類的數據點放置在簇0中,一個點放置在簇1中。將類1中的兩個數據點放置在簇2中,將一個數據點放置在簇1中。
很多的外部評價指標,都使用列聯矩陣作為其計算的基礎,了解了列聯矩陣我們開始介紹一些外部指標。
2、Adjusted Rand Index(ARI)
Rand Index (RI)[4]以William Rand命名,通過兩兩比較來衡量聚類分配與真實類標簽之間的相似性。計算簇分配和類標簽之間的一致數與總數據點對數的比值:
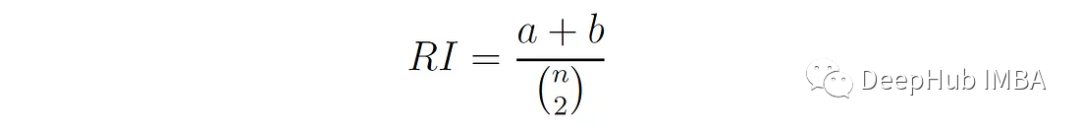
A是具有相同類標簽且屬于同一聚類的點對的數目,B是具有不同類標簽且屬于不同聚類的點對的個數。N是總點數。
RI的范圍從0到1,其中1表示簇分配和類標簽完全相同。
可以使用sklearn.metrics.rand_score()進行計算。
from sklearn.metrics import rand_score
true_labels = [0, 0, 0, 1, 1, 1]
cluster_labels = [0, 0, 1, 1, 2, 2]
print(f'RI = {rand_score(true_labels, cluster_labels):.3f}')得到:
RI = 0.667在我們的這個例子中a = 2, b = 8,因此
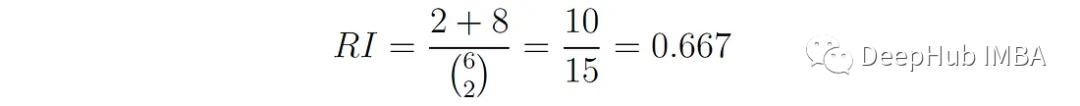
Rand Index的問題是,即使對于隨機的簇分配,它也可以得到很高的值,特別是當簇數量很大時。這是因為當聚類數量增加時,隨機將不同標簽的點分配給不同聚類的概率增加。因此特定的RI值可能是模糊的,因為不清楚分數中有多少是偶然的,多少是實際一致的。
而ARI通過將RI分數標準化來糾正這一點,考慮到隨機分配簇時的預期RI分數。計算公式如下:
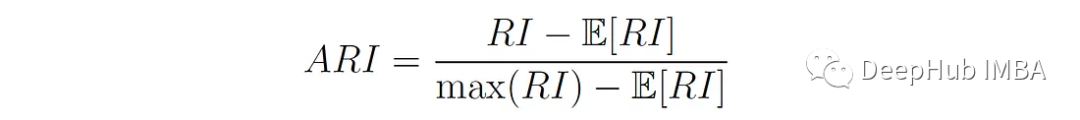
其中E[RI]為隨機聚類分配下Rand指數的期望值。該值是使用上面描述的列聯表計算的。我們首先計算表中每行和每列的和:
A?是屬于第i類的點的總數:
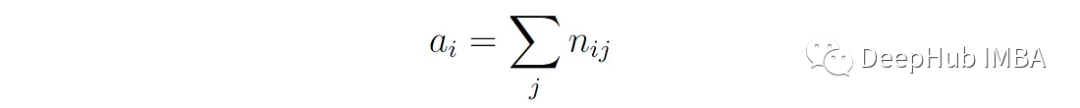
B?是分配給聚類j的總點數:
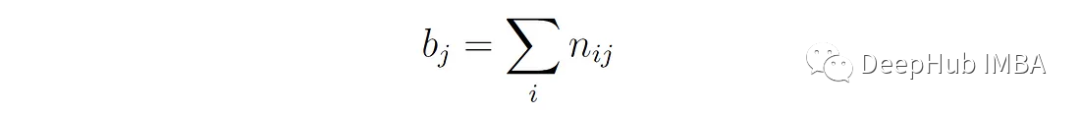
然后使用以下公式計算ARI:
分子表示如果簇分配是隨機的(E[RI]),則實際配對Rand指數與預期配對數之間的差值。分母表示最大可能的配對數(最大Rand指數)與隨機情況下的期望配對數(E[RI])之差。
規范化此值,調整數據集的大小和元素跨簇的分布。
ARI值的范圍從-1到1,其中1表示簇分配和類標簽之間完全一致,0表示隨機一致,負值表示一致性低于偶然預期。
from sklearn.metrics import adjusted_rand_score
print(f'ARI = {adjusted_rand_score(true_labels, cluster_labels):.3f}')結果如下:
ARI = 0.242獨立于類標簽的聚類賦值會得到ARI比如負值或接近0:
true_labels = [0, 0, 0, 1, 1, 1]
cluster_labels = [0, 1, 2, 0, 1, 2]
print(f'RI = {rand_score(true_labels, cluster_labels):.3f}')
print(f'ARI = {adjusted_rand_score(true_labels, cluster_labels):.3f}')結果如下:
RI = 0.400
ARI = -0.364使用我們上面創建的數據集,我們數據點有真實標簽(存儲在y變量中),所以可以使用外部評估指標來評估我們之前獲得的三個k-means聚類。這些聚類的ARI評分如下:
print(f'ARI(2 clusters): {adjusted_rand_score(y, labels_k2):.3f}')
print(f'ARI(3 clusters): {adjusted_rand_score(y, labels_k3):.3f}')
print(f'ARI(4 clusters): {adjusted_rand_score(y, labels_k4):.3f}')結果如下:
ARI(2 clusters): 0.565
ARI(3 clusters): 1.000
ARI(4 clusters): 0.864當k = 3時,得到一個完美的ARI分數,這意味著在這種情況下,簇分配和真實標簽之間存在完美匹配。
優點:
- RI分數的取值范圍是0到1,ARI分數的取值范圍是-1到1。有界范圍使得比較不同算法之間的分數變得容易。
- 對于任意數量的樣本和簇,隨機(均勻)簇分配的ARI分數都接近于0。
- ARI對機會的調整使其更加可靠和可解釋性。
- 沒有對聚類結構做任何假設,這使得這些指標對于比較不同的聚類算法非常有用,而不依賴于聚類形狀。
缺點:
- 需要有真實的標簽來確定結果
3、同質性、完整性和v測度
這些方法通過檢查聚類分配與真實類標簽的一致性來評估聚類的質量。
同質性 Homogeneity 度量每個簇是否只包含單個類的成員。
定義如下:
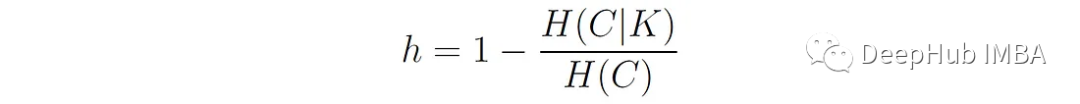
這里:
C代表真值類標簽。K表示算法分配的聚類標簽。H(C|K)是給定聚類分配的類分布的條件熵的加權平均值:
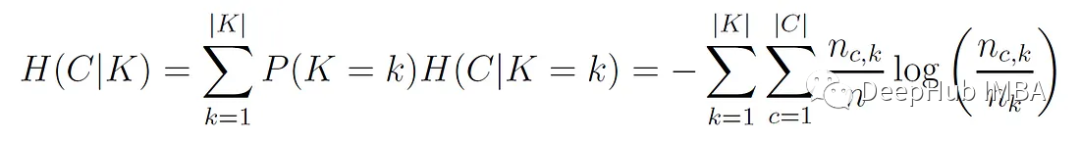
其中nc,?為分配給k簇的c類樣本數,n?為k簇的樣本數,n為總樣本數。H(C)為類分布的熵:
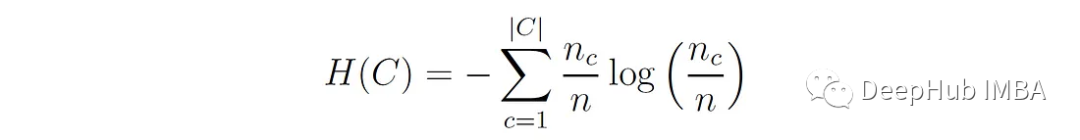
同質性評分范圍為0 ~ 1,其中1表示完全同質性,即每個簇只包含單個類的成員。
完整性 Completeness 度量給定類的所有成員是否被分配到同一個簇。
定義如下:
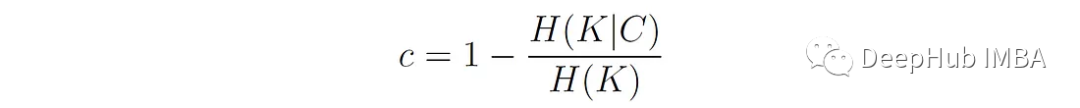
H(K|C)是給定類標簽的聚類分布條件熵的加權平均值:
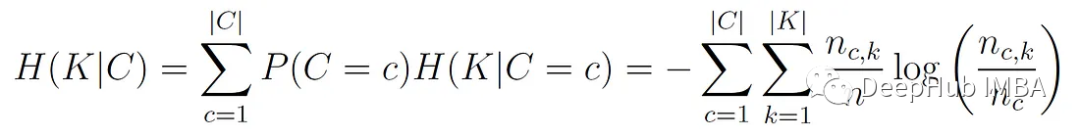
其中nc為c類的樣本數。
H(K)為聚類分布的熵:
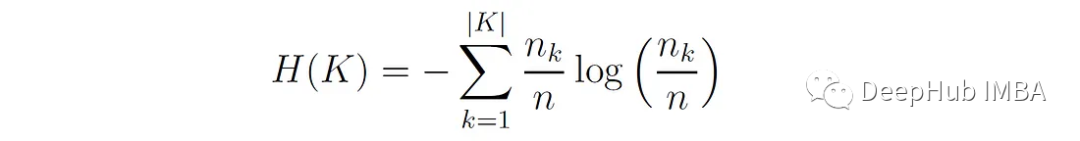
與同質性一樣,完整性的范圍從0到1,其中1表示完全完整,即每個類成員被分配到單個簇。
V-measure是同質性和完備性的調和平均值,它可以提供一個單一的分數來評估聚類性能:
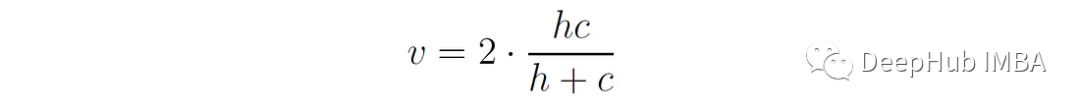
通過使用調和均值,V-measure懲罰同質性和完整性之間的不平衡,鼓勵更均勻的聚類性能。
在Scikit-Learn中可以使用sklearn.metrics中的函數homogeneity_score、completeness_score和v_measure_score來計算
from sklearn.metrics import homogeneity_score, completeness_score, v_measure_score
true_labels = [0, 0, 0, 1, 1, 1]
cluster_labels = [0, 0, 1, 1, 2, 2]
print(f'Homogeneity = {homogeneity_score(true_labels, cluster_labels):.3f}')
print(f'Completeness = {completeness_score(true_labels, cluster_labels):.3f}')
print(f'V-measure = {v_measure_score(true_labels, cluster_labels):.3f}')結果如下:
Homogeneity = 0.667
Completeness = 0.421
V-measure = 0.516將其應用在我們的示例上:
print(f'V-measure(2 clusters): {v_measure_score(y, labels_k2):.3f}')
print(f'V-measure(3 clusters): {v_measure_score(y, labels_k3):.3f}')
print(f'V-measure(4 clusters): {v_measure_score(y, labels_k4):.3f}')結果如下:
V-measure(2 clusters): 0.711
V-measure(3 clusters): 1.000
V-measure(4 clusters): 0.895當k = 3時,我們得到一個完美的V-measure分數1.0,這意味著聚類標簽與基本真值標簽完全一致。
優點:
- 提供簇分配和類標簽之間匹配的直接評估。
- 比分在0到1之間,有直觀的解釋。
- 沒有對簇結構做任何假設。
缺點:
- 不要考慮數據點在每個簇中的分布情況。
- 不針對隨機分組進行規范化(不像ARI)。這意味著取決于樣本、簇和類的數量,樣本的完全隨機分組并不總是產生相同的同質性、完備性和v度量值。因此,對于小數據集(樣本數量< 1000)或大量簇(> 10),使用ARI更安全。
4、Fowlkes-Mallows Index(FMI)
Fowlkes-Mallows Index (FMI)[5]定義為對精度(分組點對的準確性)和召回率(正確分組在一起的對的完整性)的幾何平均值:
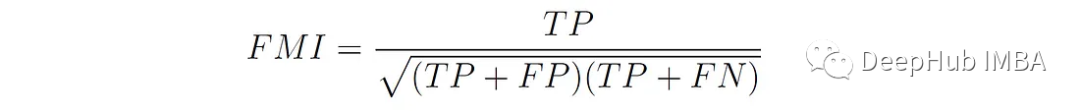
TP(True Positive)是具有相同類標簽并屬于同一簇的點對的數量。FP (False Positive)是具有不同類標簽但被分配到同一聚類的點對的數量。FN(False Negative)是具有相同類標簽但分配給不同簇的點對的數量。
FMI評分范圍為0 ~ 1,其中0表示聚類結果與真實標簽不相關,1表示完全相關。
Scikit-Learn中可以使用函數sklearn.metrics. fowlkes_malallows_score()來計算這個分數
from sklearn.metrics import fowlkes_mallows_score
true_labels = [0, 0, 0, 1, 1, 1]
cluster_labels = [0, 0, 1, 1, 2, 2]
print(f'FMI = {fowlkes_mallows_score(true_labels, cluster_labels):.3f}')結果:FMI = 0.471,在本例中,TP = 2, FP = 1, FN = 4,則:
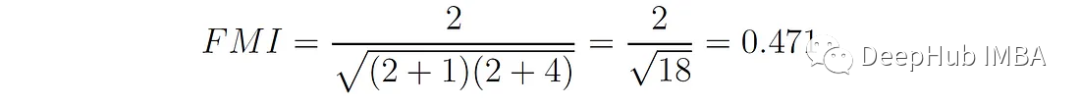
將其應用到我們的示例:
print(f'FMI(2 clusters): {v_measure_score(y, labels_k2):.3f}')
print(f'FMI(3 clusters): {v_measure_score(y, labels_k3):.3f}')
print(f'FMI(4 clusters): {v_measure_score(y, labels_k4):.3f}')結果如下:
FMI(2 clusters): 0.711
FMI(3 clusters): 1.000
FMI(4 clusters): 0.895當k = 3時,得到了一個完美的FMI分數,這表明聚類分配與基本真值標簽完全一致。
優點:
- 同時考慮準確率和召回率,提供一個平衡的聚類性能視圖。
- 比分在0到1之間。
- 對于任意數量的樣本和簇,隨機(均勻)標簽分配的FMI得分接近于0。
- 不對簇結構做假設。
缺點:
- 它是基于對元素的分析,這可能無法捕捉到簇更廣泛的結構特性,比如它們的形狀或分布。
- 當數據集高度不平衡(即一個類主導數據集)時,FMI可能無法準確反映聚類的有效性。
總結
下表總結了本文討論的不同指標和特點: