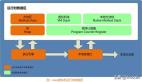
內(nèi)存模型為何要同時設(shè)計“棧區(qū)”與“堆區(qū)”?
如題,還有為啥是棧和堆,而不是隊列或者其他什么數(shù)據(jù)結(jié)構(gòu)?這就是本文要說的。
一、棧與堆簡介
在回答上述問題前,先要明確什么是“棧”,什么又是“堆”。所謂棧就是一種一維的“線性表”,而“堆”則是二維的完全二叉樹。不難看出棧相比于堆是一種更簡單的數(shù)據(jù)結(jié)構(gòu),這也是其被用于內(nèi)存模型的原因之一,夠簡單,所以其創(chuàng)建成本就很低,進而內(nèi)存的使用性能就可以提升上去。而堆作為一種完全二叉樹,同時具有“順序結(jié)構(gòu)”的特點,這就讓其在處理大量數(shù)據(jù)的排序時擁有更好的性能。
 圖片
圖片
二、棧相比隊列的優(yōu)勢
前面說棧結(jié)構(gòu)簡單,難免不讓人想到隊列,相比較起來,隊列結(jié)構(gòu)似乎更簡單一點,就算沒有更簡單也絕不比棧復(fù)雜,那憑什么不用隊列而用棧呢?
隊列無法取代棧用作內(nèi)存模型就是因為它太簡單了,“先進先出”的數(shù)據(jù)結(jié)構(gòu),就只能先進先出。而棧雖然常被描述為“先進后出”型數(shù)據(jù)結(jié)構(gòu),但實際卻并非看上去那么簡單,而是可以讓多個元素在入棧順序相同的情況下,根據(jù)需求產(chǎn)生各種不同的出棧順序。
 圖片
圖片
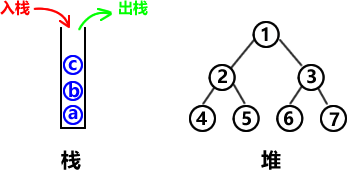
比如有a、b、c三個元素依次進棧,問出棧順序是怎樣的?依據(jù)先進后出的原則,很多人應(yīng)該馬上會想到c、b、a的出棧順序,其實還可以仍舊是a、b、c的順序出棧,和入棧順序是一樣的。這是不是違背了“先進后出”原則呢?其實沒有。
認為a、b、c的進棧順序和出棧順序一樣是違背了“先進后出”原則是因為把三個元素捆綁在一起去看了,但是分別去看就會發(fā)現(xiàn)并沒有違背先進后出。我們可以讓a進棧之后立刻出棧,然后b進棧再出棧,最后讓c進棧然后出棧,基于此種操作,你就會發(fā)現(xiàn)a、b、c的進棧順序和出棧順序一樣,同時每個元素單獨來看仍舊是“先進后出”的。
想得簡單一點,棧就是一個口袋,往里面放東西和取東西的順序自由度是很高的,這就讓棧在擁有與隊列差不多的簡單結(jié)構(gòu)易于被創(chuàng)建的同時,擁有更強大的可操作性。而隊列則像是一個垂直懸空放置且沒有封堵出口的管道,第一個進去的必然第一個出來,沒有其他的可能性,這種過于簡單的結(jié)構(gòu)缺乏可操作性,所以落選內(nèi)存模型的數(shù)據(jù)結(jié)構(gòu)設(shè)計。
三、堆的優(yōu)勢
如果只是管理非常小的內(nèi)存,棧已經(jīng)是個足夠好的數(shù)據(jù)結(jié)構(gòu)了,這里說的“小”指的是1M到2M這種規(guī)模,而這種規(guī)模顯然與實際不符,實際的主流內(nèi)存已經(jīng)達到8G以上了,那剩下的那些內(nèi)存如何管理的呢?它們則主要依靠堆結(jié)構(gòu)管理(是主要不是全部)。前面說了堆是一種完全二叉樹,也就是除了最后一層外其他層全是滿結(jié)點的二叉樹,而且更重要的是它還是“順序結(jié)構(gòu)”的。
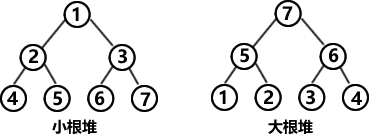
說堆是一種“順序結(jié)構(gòu)”的完全二叉樹,意思就是說,假如用“中序遍歷”對其進行從根到葉子的遍歷,將會得到“整體有序”的隊列。再說得通俗一點就是,我們知道一棵大的二叉樹往往是由若干小的二叉樹組合而成的,然后在這樣一種結(jié)構(gòu)中,我們會看到里面所有的父結(jié)點的值一定都是大于其左、右子結(jié)點的,這被稱為大根堆。還有一種情況是所有父結(jié)點都是小于其左、右子結(jié)點的,這被稱為小根堆。
 圖片
圖片
這時我們會看到堆不光因為其完全二叉樹的結(jié)構(gòu)像一個金字塔,其每層的值也是如金字塔一樣,從底部開始一層比一層大,直到根節(jié)點是最大值,即大根堆。或者從底層開始一層比一層小,直到根節(jié)點是最小值,即小根堆。
因為堆的這種順序結(jié)構(gòu),導(dǎo)致其在處理龐大的數(shù)據(jù)排序時具有更好的性能,“堆排序”本身就是一種典型的處理大量數(shù)據(jù)的選擇排序算法。而高效的排序則意味著可以更快地基于有序隊列進行高效的查找,進而從整體上提升查找的效率。這就彌補了棧結(jié)構(gòu)在大規(guī)模使用,管理過大內(nèi)存后的性能短板。
四、棧與堆的取長補短
但是堆作為一種相對復(fù)雜的數(shù)據(jù)結(jié)構(gòu),其創(chuàng)建過程明顯比棧復(fù)雜,這導(dǎo)致它在處理少量的簡單類型數(shù)據(jù)時,其性能反而不如棧,這里的短板則由棧來彌補。于是內(nèi)存模型就同時設(shè)計了棧與堆,二者配合使用取長補短。