四種SVM主要核函數及相關參數的比較
本文將用數據可視化的方法解釋4種支持向量機核函數和參數的區別
簡單地說,支持向量機(SVM)是一種用于分類的監督機器學習技術。它的工作原理是計算一個最好地分隔類的最大邊距的超平面。

支持向量機除了提供簡單的線性分離之外,還可以通過應用不同的核方法進行非線性分類。參數設置也是SVM更好地工作的另一個重要因素。通過適當的選擇,我們可以使用支持向量機來處理高維數據。
本文旨將使用Scikit-learn庫來展示每個核函數以及如何使用不同的參數設置。并且通過數據可視化進行解釋和比較。
如果你正在尋找常見數據集(如Iris Flowers或Titanic)之外的另一個數據集,那么poksammon數據集可以是另一個選擇。盡管你可能不是這些口袋怪物的粉絲,但它們的屬性很容易理解,并且有各種各樣的特征可供使用。
Pokemon的屬性,如hp,攻擊和速度,可以作為連續變量使用。對于分類變量,有類型(草、火、水等)、等級(普通、傳奇)等。此外,如果有新一代或Pokemon出現,數據集將在未來進行更新。
免責聲明:Pokemon和所有相關名稱均為任天堂公司的版權和商標。
導入數據和庫
為了直觀地展示每個SVM的內核是如何分離分類的的,我們將只選擇baby, legendary, mythical。我們先從導入數據和庫開始。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('pokemons.csv', index_col=0)
df.reset_index(drop=True, inplace=True)
df = df[df['rank'].isin(['baby', 'legendary'])]
df.reset_index(drop=True, inplace=True)
df.head()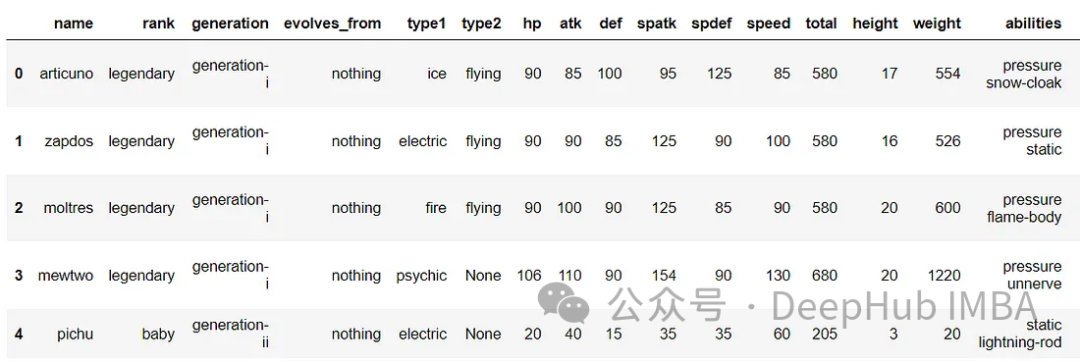
EDA
Pokemon有7種基本的屬性- hp,攻擊,防御,特殊攻擊,特殊防御,速度和高度。下面的步驟是使用我們選擇的統計數據執行一個快速EDA。
select_col = ['hp','atk', 'def', 'spatk', 'spdef', 'speed', 'height']
df_s = df[select_col]
df_s.info()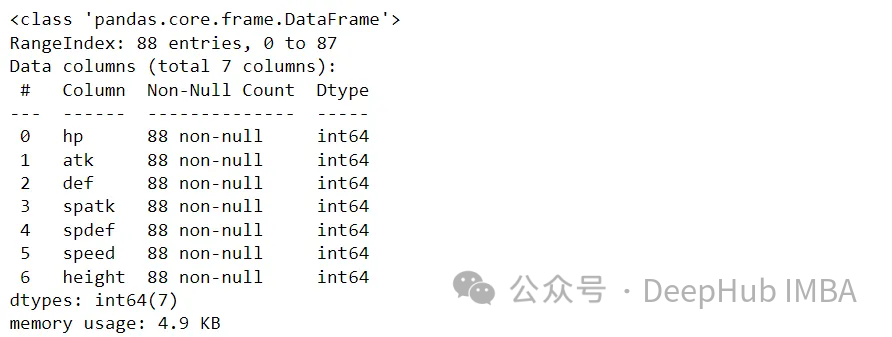
幸運的是,沒有空值。接下來,讓我們繪制Box和Whisker圖,以查看這些變量的分布。
sns.set_style('darkgrid')
df_s.iloc[:,].boxplot(figsize=(11,5))
plt.show()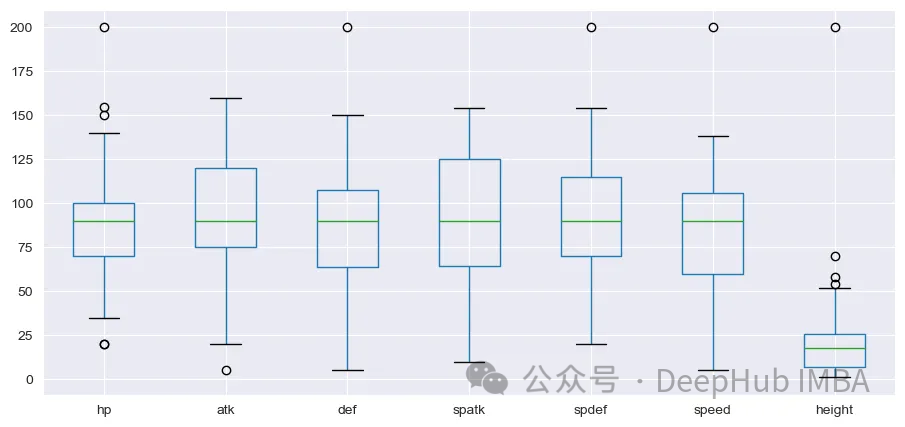
height變量的分布與其他變量有很大的不同。在繼續之前應該執行標準化。我們將使用來自sklearn的StandardScaler來進行處理
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
array_s = scaler.fit_transform(df_s)
df_scal = pd.DataFrame(array_s, columns=[i+'_std' for i in select_col])
df_scal.boxplot(figsize=(11,5))
plt.show()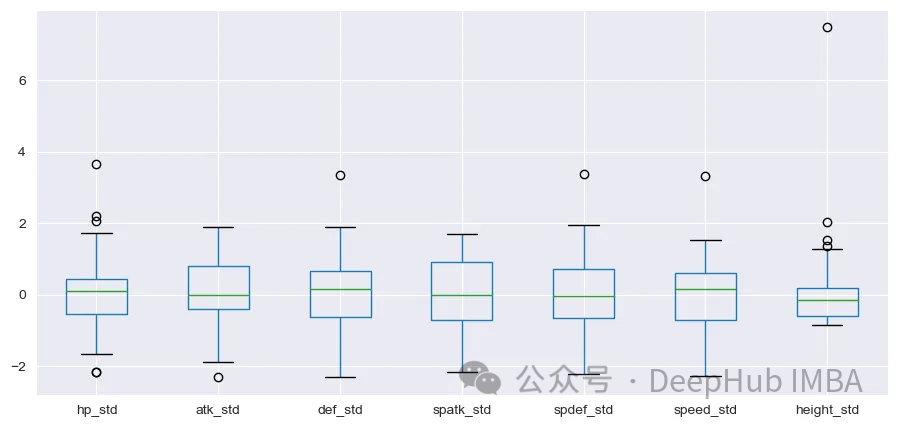
標準化之后,分布看起來更好。
由于我們的數據集有多個特征,我們需要進行降維繪圖。使用來自sklearn.decomposition的類PCA將維數減少到兩個。結果將使用Plotly的散點圖顯示。
from sklearn.decomposition import PCA
import plotly.express as px
#encoding
dict_y = {'baby':1, 'legendary':2}
df['s_code'] = [dict_y.get(i) for i in df['rank']]
df.head()
pca = PCA(n_compnotallow=2)
pca_result = pca.fit_transform(array_s)
df_pca = pd.DataFrame(pca_result, columns=['PCA_1','PCA_2'])
df = pd.concat([df, df_pca], axis=1)
fig = px.scatter(df, x='PCA_1', y='PCA_2', hover_name='name',
color='rank', opacity=0.9,
color_discrete_sequence=['red', 'blue'])
fig.update_xaxes(showgrid=False)
fig.update_yaxes(showgrid=False)
fig.show()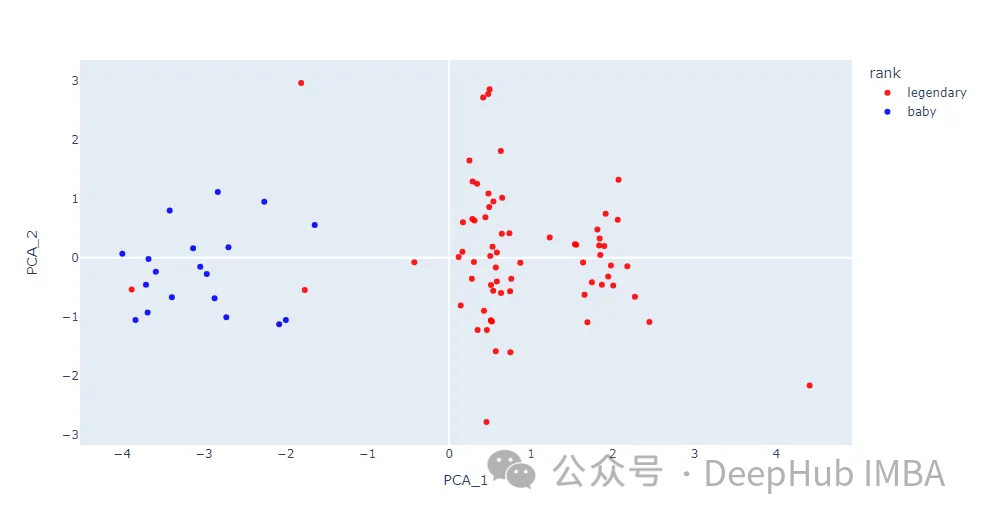
我們把Pokemon圖片帶入散點圖。

再次免責聲明:Pokemon和所有相關名稱均為任天堂公司的版權和商標。
baby和legendary這兩個類別之間的大多數數據點是分開的。盡管這兩個類并沒有完全分離,但在本文中對每個內核函數進行實驗還是很有用的。
下一步是在三維空間中獲得更多細節。讓我們將PCA組件的數量更改為三個。這是3D散點圖可以顯示的最大數字。
pcaz = PCA(n_compnotallow=3)
pcaz_result = pcaz.fit_transform(array_s)
df_pcaz = pd.DataFrame(pcaz_result, columns=['PCAz_1', 'PCAz_2', 'PCAz_3'])
df = pd.concat([df, df_pcaz], axis=1)
fig = px.scatter_3d(df, x='PCAz_1', y='PCAz_2', z='PCAz_3', hover_name='name',
color='rank', opacity=0.9,
color_discrete_sequence=['red', 'blue'])
fig.update_traces(marker=dict(size=4))
fig.update_layout(margin=dict(l=0, r=0, t=0, b=0))
fig.show()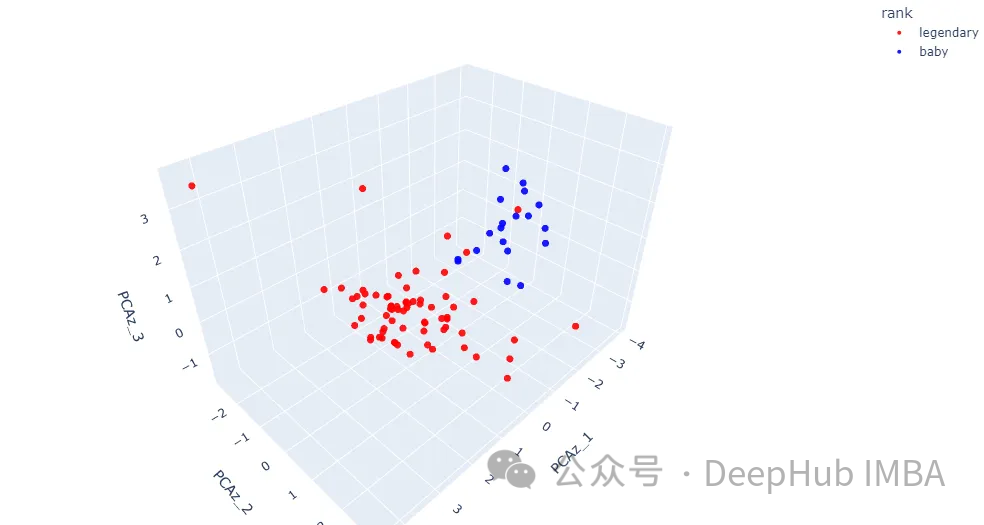
結果顯示了更多關于數據點如何在三維空間中定位的細節。在一些區域兩個類仍然混合在一起。下面我們討論核方法。
核方法
支持向量機可以簡單地使用Scikit-learn庫中的sklearn.svm.SVC類執行。可以通過修改核參數來選擇核函數。總共有五種方法可用:
Linear
Poly
RBF (Radial Basis Function)
Sigmoid
Precomputed本文將主要關注前四種核方法,因為最后一種方法是預計算的,它要求輸入矩陣是方陣,不適合我們的數據集
除了核函數之外,我們還將調整三個主要參數,以便稍后比較結果。
C:正則化參數
Gamma(γ): rbf、poly和sigmoid函數的核系數
Coef0:核函數中的獨立項,只在poly和s型函數中有意義
在下面的代碼中,predict_proba()將計算網格上可能結果的概率。最終結果將顯示為等高線圖。
from sklearn import svm
import plotly.graph_objects as go
y = df['s_code'] # y values
h = 0.2 # step in meshgrid
x_min, x_max = df_pca.iloc[:, 0].min(), df_pca.iloc[:, 0].max()
y_min, y_max = df_pca.iloc[:, 1].min(), df_pca.iloc[:, 1].max()
xx, yy = np.meshgrid(np.arange(x_min-0.5, x_max+0.5, h), #create meshgrid
np.arange(y_min-0.5, y_max+0.5, h))
def plot_svm(kernel, df_input, y, C, gamma, coef):
svc_model = svm.SVC(kernel=kernel, C=C, gamma=gamma, coef0=coef,
random_state=11, probability=True).fit(df_input, y)
Z = svc_model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 0]
Z = Z.reshape(xx.shape)
fig = px.scatter_3d(df, x='PCAz_1', y='PCAz_2', z='PCAz_3', #3D Scatter plot
hover_name='name',
color='rank', opacity=0.9,
color_discrete_sequence=['red', 'blue'])
fig.update_traces(marker=dict(size=4))
fig.add_traces(go.Surface(x=xx, y=yy, # prediction probability contour plot
z=Z+round(df.PCAz_3.min(),3), # adjust the contour plot position
name='SVM Prediction',
colorscale='viridis', showscale=False,
contours = {"z": {"show": True, "start": x_min, "end": x_max,
"size": 0.1}}))
title = kernel.capitalize() + ' C=' + str(i) + ', γ=' + str(j) + ', coef0=' + str(coef)
fig.update_layout(margin=dict(l=0, r=0, t=0, b=0), showlegend=False,
title={'text': title,
'font':dict(size=39),
'y':0.95,'x':0.5,'xanchor': 'center','yanchor': 'top'})
return fig.show()最后,創建三個參數的列表以進行比較,這里將比較0.01和100之間的值。如果您想嘗試不同的值,可以調整該數字。
from itertools import product
C_list = [0.01, 100]
gamma_list = [0.01, 100]
coef_list = [0.01, 100]
param = [(r) for r in product(C_list, gamma_list, coef_list)]
print(param)
現在一切都準備好了,讓我們用不同類型的核函數繪制結果。
1、線性核
這是最常見、最簡單的SVM的核函數。這個核函數返回一個線性超平面,它被用作分離類的決策邊界。通過計算特征空間中兩個輸入向量的點積得到超平面。
for i,j,k in param:
plot_svm('linear', df_pca, y, i, j, k)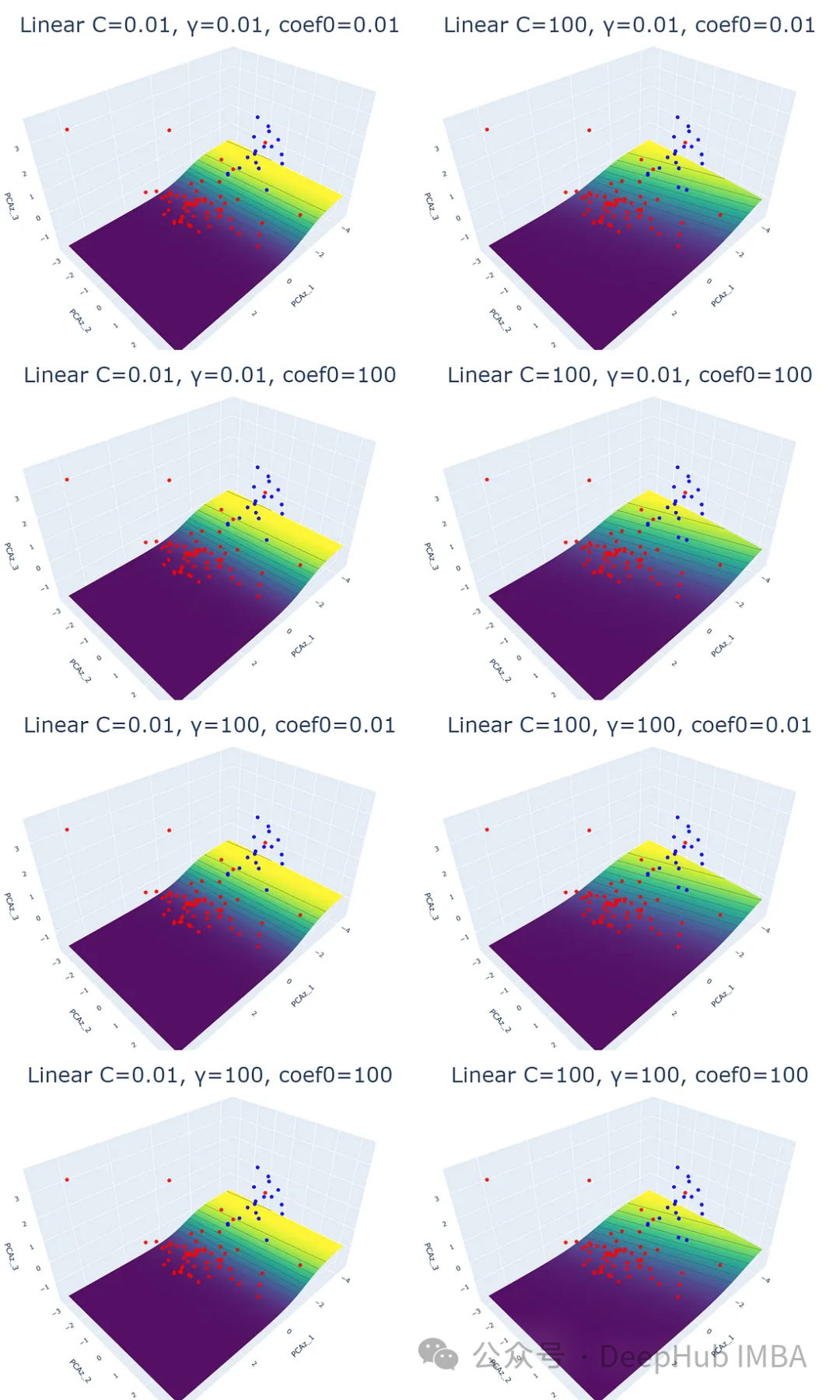
結果中的平面(等高線圖)不是超平面。它們是predict_proba()的預測概率的結果,其值在0到1之間。
概率平面表示數據點被分類的概率。黃色區域意味著成為Baby可能性很大,而藍色區域則表示成為Legend的可能性很大。
改變SVM結果的唯一參數是正則化參數(C)。理論上,當C的數量增加時,超平面的裕度會變小。當來自不同類別的數據點混合在一起時,使用高C可能會很好。過高的正則化會導致過擬合。
2、徑向基函數(RBF)核
RBF(徑向基函數)。該核函數計算歐幾里得距離的平方來度量兩個特征向量之間的相似性。
只需更改內核名稱,就可以使用相同的for循環進程。
for i,j,k in param:
plot_svm('rbf', df_pca, y, i, j, k)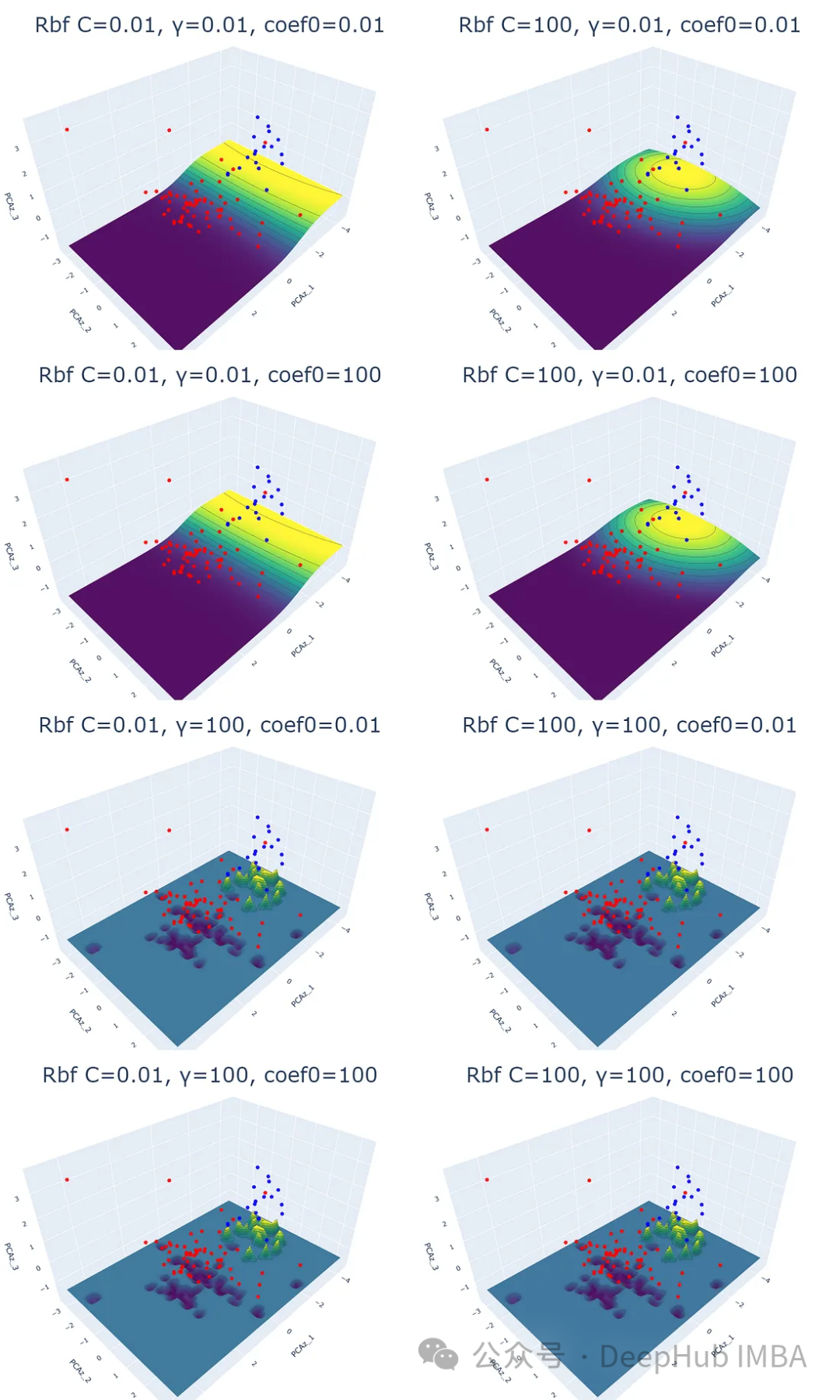
結果表明,除了正則化參數(C)外,γ (γ)也會影響RBF核的結果,coef0對RBF核函數沒有影響。
伽馬參數決定了數據點對超平面的影響。對于高伽馬值,靠近超平面的數據點將比更遠的數據點有更大的影響。
低伽馬值的概率平面比高伽馬值的概率平面平滑。結果在高伽馬值的后4個散點圖中更為明顯;每個數據點對預測概率影響很大。
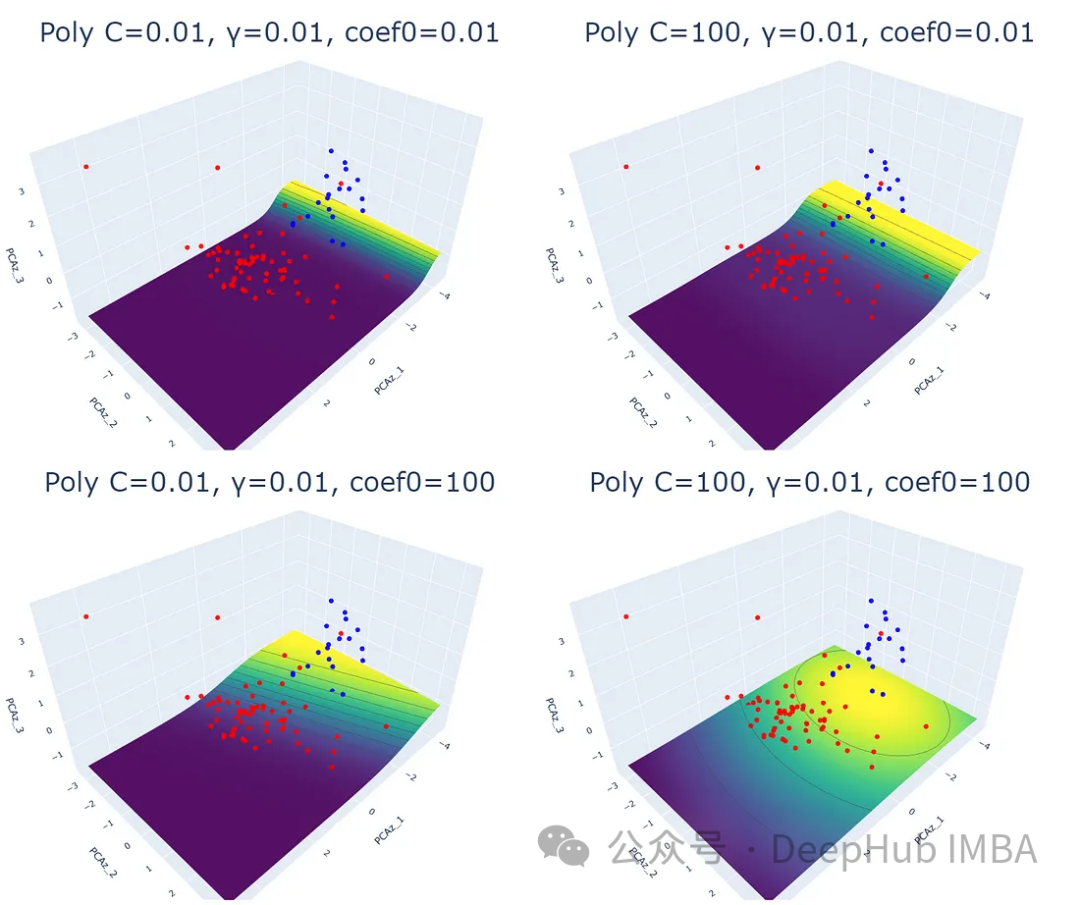
3、多項式核
多項式核通過將數據映射到高維空間來工作。取變換后的高維空間中數據點與原始空間的點積。由于它處理高維數據的能力,這個內核被推薦用于執行非線性分離。
多項式核與其他核相比,處理時間是最長的。這可能是將數據映射到高維空間的結果。
for i,j,k in param:
plot_svm('poly', df_pca, y, i, j, k)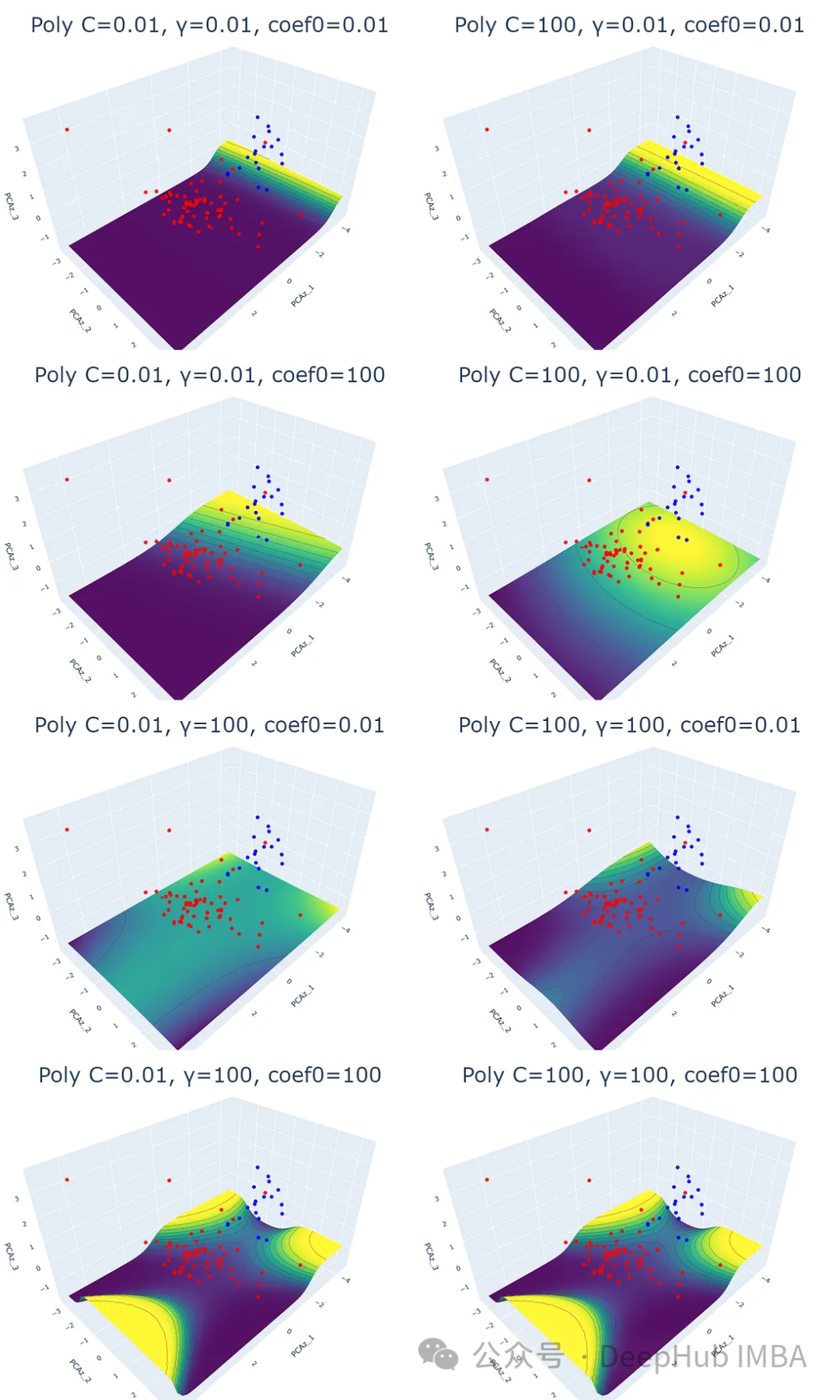
可以看出,這三個參數都會影響SVM的分類效果。除正則化參數(C)和γ (γ)外,coef0參數控制高次多項式對模型的影響程度。coef0值越高,預測概率等高線越趨于彎曲。
4、Sigmoid核
理論上,sigmoid函數擅長映射輸入值并返回0到1之間的值。該函數通常用于神經網絡中,其中s形函數作為分類的激活函數。
盡管它可以應用于SVM任務并且看起來很有用,但一些文章說結果可能太復雜而無法解釋。我們這里使用數據可視化來查看這個問題。
for i,j,k in param:
plot_svm('sigmoid', df_pca, y, i, j, k)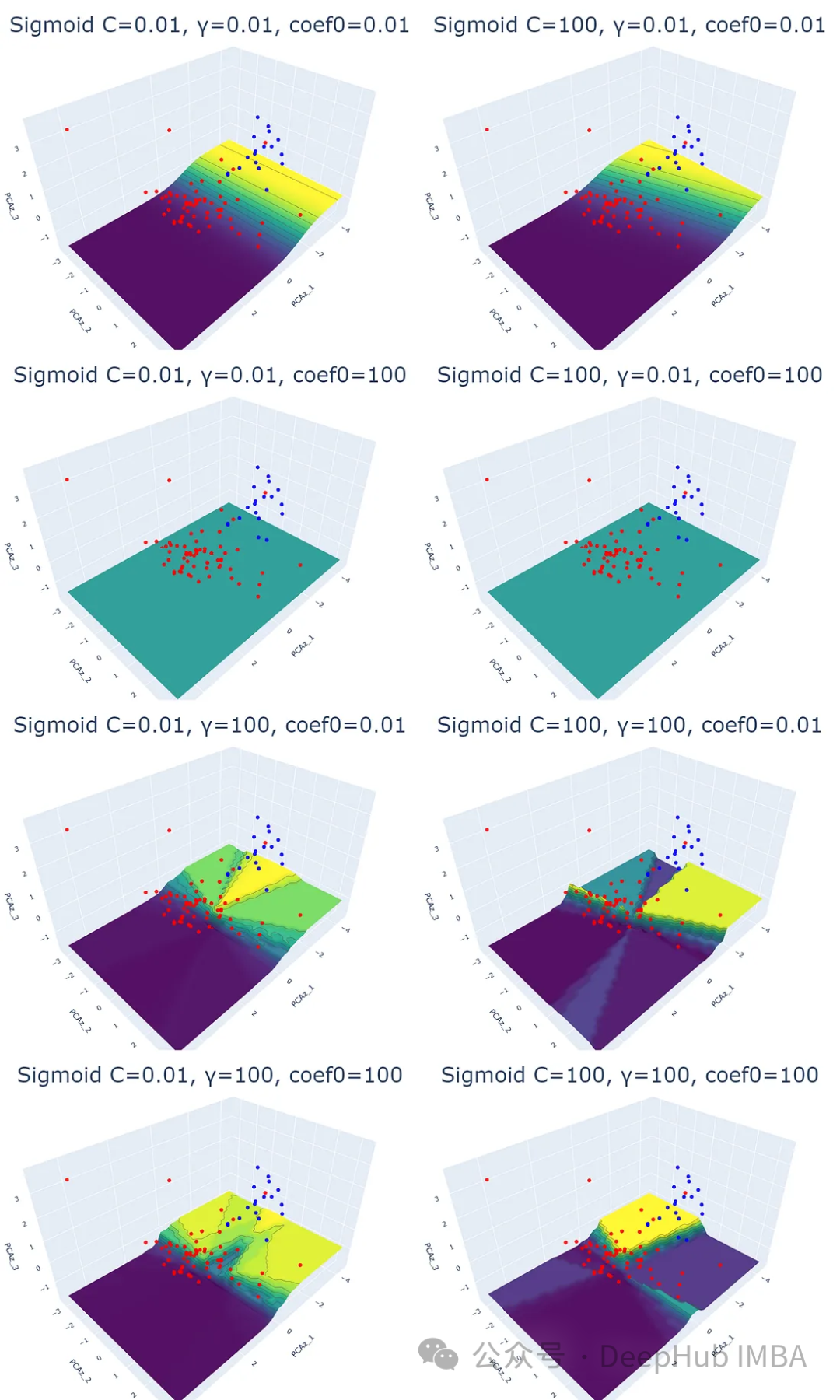
可以看到從Sigmoid核得到的圖很復雜,也無法解釋。預測概率等值線圖與其他核的預測概率等值線圖完全不同。并且等高線圖的顏色不在它對應的數據點下面。最主要的是當改變參數值時,結果沒有模式可循。
但是我個人認為,這并不意味著這個內核很糟糕或者應該避免使用。也許他找到了我們未察覺的數據特征,所以可能會有一些分類任務,sigmoid將適合使用。
總結
支持向量機是一種有效的機器學習分類技術,因為它能夠提供簡單的線性和非線性分類。
因為每個數據集都有不同的特征,所以不存在銀彈。為了使支持向量機有效,必須選擇好核和參數,同時還要注意避免過擬合,我們以上的總結希望對你的選擇有所幫助。