一文帶您了解偽對數(Pseudo-Log):可視化傾斜數據的黃金方法
偏斜數據是指分布高度不均勻的數據:當變量數據顯示為直方圖時,大部分數據點要么聚集在分布的左側,長尾向右延伸(右偏斜),要么反之(左偏斜),或呈現更復雜的偏斜模式。偏斜數據對可視化,特別是熱力圖的繪制,提出了很大的挑戰。通常情況下,人們會使用對數變換來處理這些數據。然而,經典對數變換無法處理零或負數,而偽對數變換則能夠更好地處理和可視化這些數據。
為什么使用偽對數?
經典對數對零和負值無定義,這限制了其在許多應用中的使用。相比之下,偽對數(Pseudo-Logarithm)修正了經典對數的這一限制:它對所有實數都有定義,對于大絕對值使用帶符號的對數,并在底數趨近于零時平滑過渡到零。
以10為底的偽對數(pseudo-log10)的定義是:
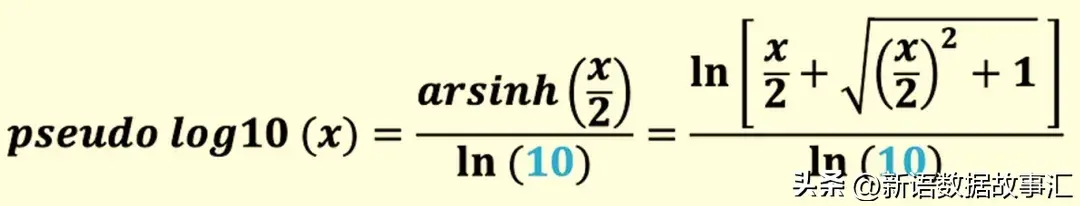
在下面的代碼和圖中,x軸上的值通過偽對數10變換映射到y軸上,用藍線表示。相比之下,經典的對數10變換則用黑線繪制。
import numpy as np
import matplotlib.pyplot as plt
# 偽對數10變換函數
def pseudo_log10(x):
return np.log(x/2+np.sqrt(x*x/4+1))/np.log(10)
# 定義數據
x = np.linspace(-15, 15, 400)
y_pseudo_log10 = pseudo_log10(x)
y_log10 = np.log10(x[200:])
# 創建圖形
plt.figure(figsize=(10, 6))
# 繪制偽對數10變換的曲線,繪制經典對數10變換的曲線
plt.plot(x, y_pseudo_log10, label='Pseudo-log10 Transformation', color='blue')
plt.plot(x[200:], y_log10, label='Classic log10 Transformation', color='black')
# 添加圖例
plt.legend()
# 添加標題和標簽
plt.title('Comparison of Pseudo-log10 and Classic log10 Transformations')
plt.xlabel('x')
plt.ylabel('Transformed value')
# 顯示圖形
plt.grid(True)
plt.show()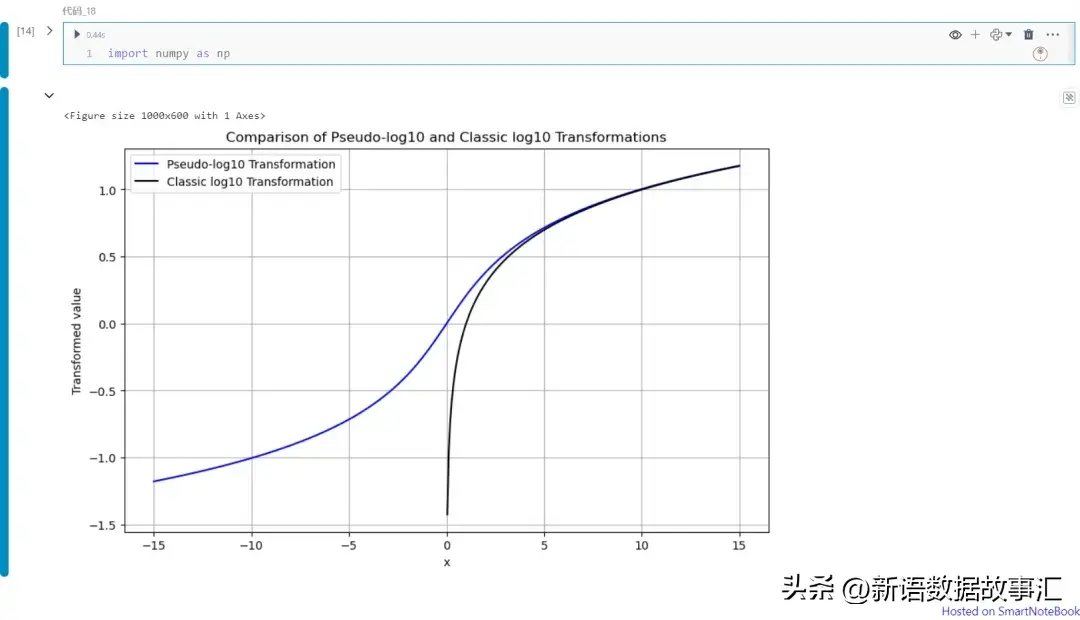
該圖展示了偽對數變換的一些良好特性:
- 偽 log10(x) 在所有實數上都有定義。
- 偽 log10(0) = 0
- 如果 x ? 0,則偽 log10(x) ≈ log10(x)
- 如果 x ? 0,則偽 log10(x) ≈ ?log10(|x|)
類似地,任何底數為b的偽對數(偽對數b)可定義如下:
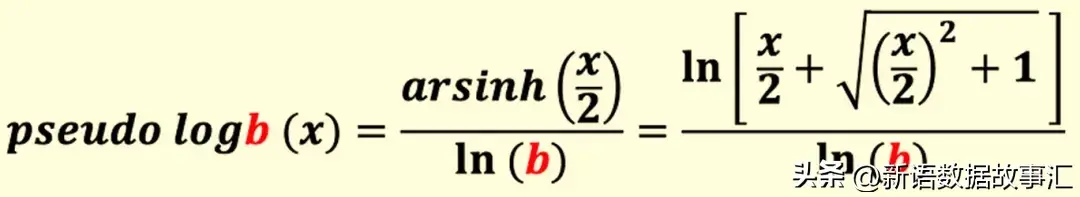
偽對數b (x) 具有以下性質:
- 偽對數b (0) = 0
- 如果 x ? 0,則偽對數b (x) ≈ log b (x)
- 如果 x ? 0,則偽對數b (x) ≈ ?log b (|x|)
數據可視化中的偽對數
對數變換是處理廣泛分布數據的常用方法。它將數據轉換為更規范的分布,從而更容易可視化。我們先看一下對數變換和偽對數變換對分布的影響(沒有找到合適的數據,下面數據是生成的):
import numpy as np
import matplotlib.pyplot as plt
# 生成1000個來自右偏分布的樣本
data = np.random.exponential(scale=2, size=1000)
# 定義偽對數變換函數
def pseudo_log(x):
return np.log(x/2+np.sqrt(x*x/4+1))/np.log(10)
# 對數據應用變換
log_data = np.log(data)
pseudo_log_data = pseudo_log(data)
# 繪制原始數據、對數變換數據和偽對數變換數據
plt.figure(figsize=(12, 8))
# 繪制原始數據
plt.subplot(3, 1, 1)
plt.hist(data, bins=50, color='blue', alpha=0.7, label='Original Data')
plt.legend()
plt.title('Original Data')
# 繪制對數變換數據
plt.subplot(3, 1, 2)
plt.hist(log_data, bins=50, color='green', alpha=0.7, label='Log-Transformed Data')
plt.legend()
plt.title('Log-Transformed Data')
# 繪制偽對數變換數據
plt.subplot(3, 1, 3)
plt.hist(pseudo_log_data, bins=50, color='red', alpha=0.7, label='Pseudo-Log-Transformed Data')
plt.legend()
plt.title('Pseudo-Log-Transformed Data')
plt.tight_layout()
plt.show()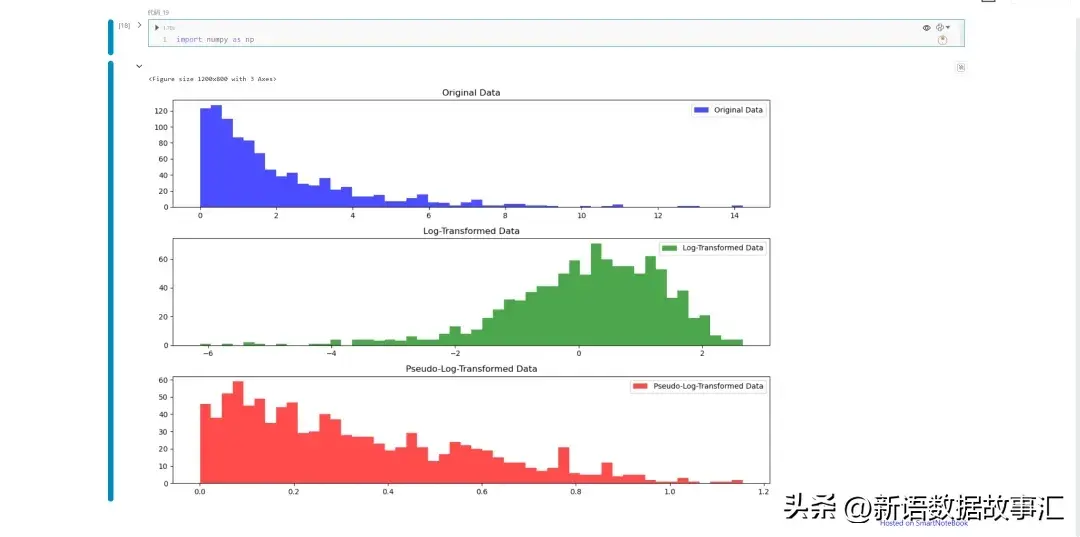
偽對數變換對熱力圖可視化的效果影響:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Simulate some population density data with a wider range
np.random.seed(42)
data = np.concatenate([np.random.lognormal(mean=0, sigma=2.0, size=(10, 20)),
0-np.random.lognormal(mean=0, sigma=2.0, size=(10, 20))])
# Function to plot the heatmaps
def plot_heatmaps(data):
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# Linear color scale
sns.heatmap(data, ax=axes[0], cmap='viridis', cbar_kws={'label': 'population density / km2'})
axes[0].set_title('Linear color scale')
# Log10 transformation
log_data = np.log10(data + 1)
sns.heatmap(log_data, ax=axes[1], cmap='viridis', cbar_kws={'label': 'log10(population density / km2)'})
axes[1].set_title('log10 transformation')
# Pseudo-log transformation (log + sqrt)
pseudo_log_data = np.log(data + np.sqrt(data**2 + 1))
sns.heatmap(pseudo_log_data, ax=axes[2], cmap='viridis', cbar_kws={'label': 'pseudo-log(population density / km2)'})
axes[2].set_title('pseudo-log transformation')
plt.tight_layout()
plt.show()
plot_heatmaps(data)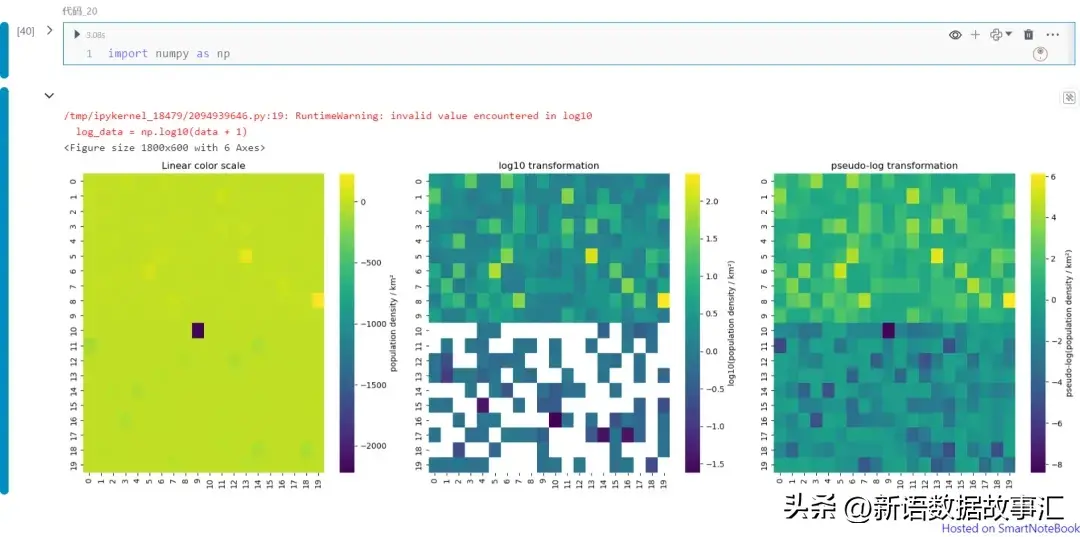
下圖是https://www.databrewer.co/blog/pseudo-log-transformation 上面的R語言生成的示例圖:
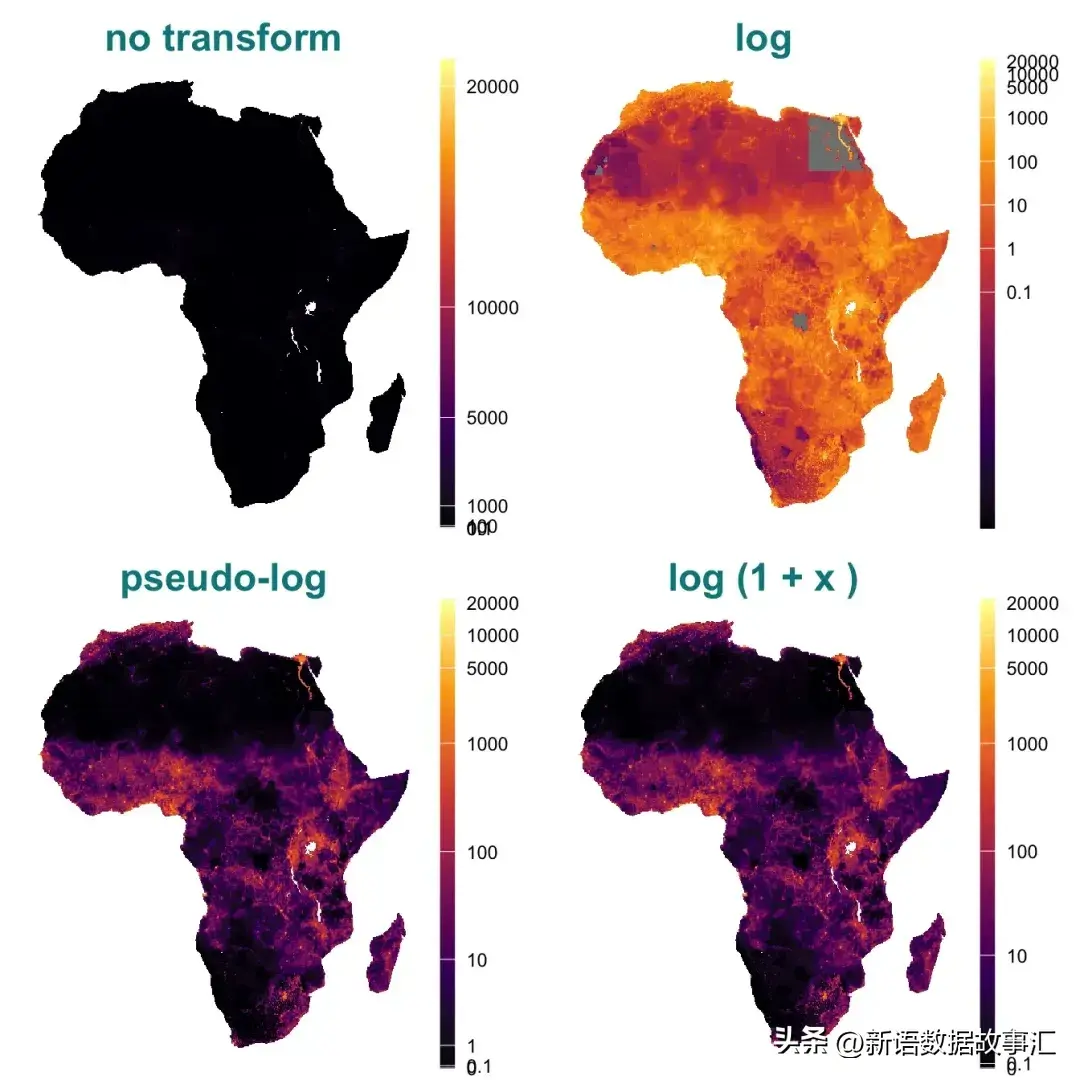
偏斜數據是分布不均的數據,對可視化,特別是熱力圖繪制提出了挑戰。經典對數變換不能處理零和負數,而偽對數變換可以應對這一問題。偽對數在所有實數上都有定義,并能平滑過渡。本文通過比較偽對數和經典對數變換,展示了偽對數在處理和可視化偏斜數據中的優越性。通過實例數據,顯示偽對數變換能夠有效地改善數據分布和可視化效果,使得數據展示更加清晰。