深度學習中常見的權重初始化方法
今天給大家分享常見的 7 種權重初始化方法
初始化深度學習模型的權重是影響模型訓練速度、穩定性以及最終性能的重要因素。
以下是常見的 7 種權重初始化方法,每種方法都有其適用的場景和特性。
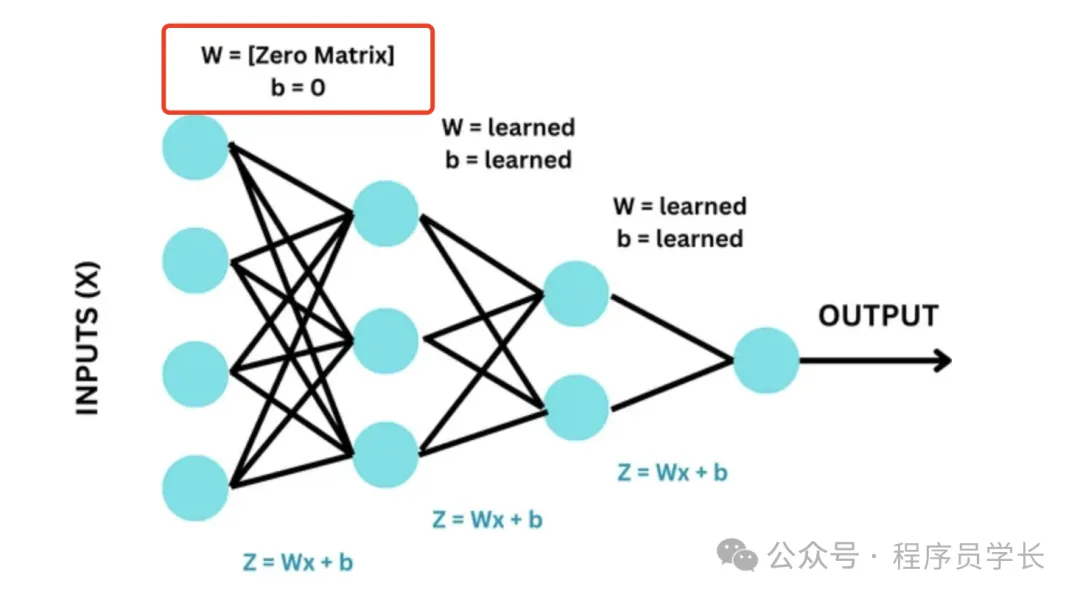
1. 零初始化(Zero Initialization)
將所有權重初始化為零。這是最簡單的初始化方法,但通常不適用于深度神經網絡。
優點
實現簡單,易于理解。
缺點
這種初始化方法的問題在于,會導致所有的神經元在每一層都學習到相同的特征。
因為對于對稱的權重,反向傳播更新時會導致相同的梯度,這使得所有的神經元在訓練過程中沒有差異化,從而喪失了模型的學習能力。
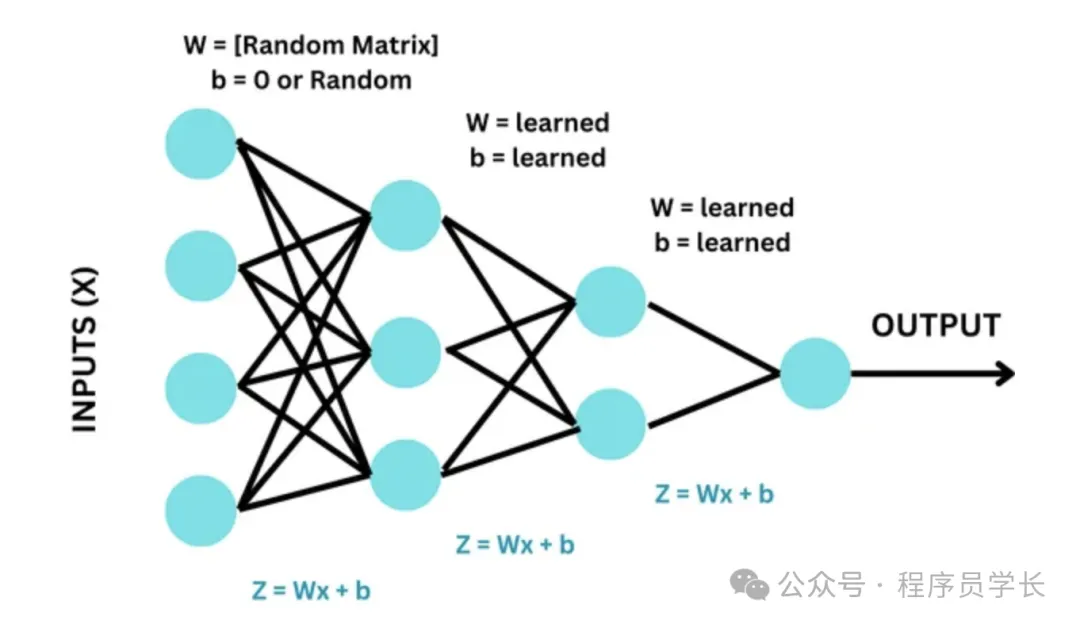
2.隨機初始化(Random Initialization)
權重隨機初始化為一個較小的隨機數。通常,這些隨機數從均勻分布或正態分布中采樣。
優點:
可以打破對稱性,避免零初始化帶來的問題。
缺點:
需要小心選擇隨機數的范圍,太大可能導致梯度爆炸,太小則可能導致梯度消失。
3.Xavier 初始化(Xavier Initialization)
Xavier 初始化方法根據輸入和輸出的節點數來選擇權重的初始值范圍,使得網絡中每一層的輸入和輸出的方差保持一致,避免梯度爆炸或消失。
公式
- 若使用均勻分布:
- 若使用正態分布:
優點
- 在深層網絡中,Xavier 初始化可以平衡前向和反向傳播中的信號,從而加速收斂。
- 適用于Sigmoid 和 tanh激活函數的網絡。
缺點
對于激活函數是ReLU的網絡,Xavier 初始化可能不夠有效。
4.He初始化(He Initialization)
He 初始化是專門為 ReLU 及其變體(如Leaky ReLU)激活函數設計的初始化方法。
它在Xavier初始化的基礎上,將方差放大,以適應ReLU激活函數。
公式
- 若使用正態分布:
- 若使用均勻分布:
優點
更適合ReLU激活函數,能有效避免梯度消失問題。
缺點
對于其他非ReLU激活函數,可能不如Xavier初始化效果好。
5.LeCun 初始化(LeCun Initialization)
LeCun 初始化是一種專門為特定激活函數(如 tanh 和 Leaky ReLU)設計的權重初始化方法。
它的目標是確保在前向傳播和反向傳播中,網絡中信號的方差能夠保持穩定,從而避免梯度消失或爆炸問題。
公式
LeCun 初始化的方法是基于正態分布對權重進行初始化,其標準差與輸入神經元的數量 相關
優點
能有效保持網絡中信號的方差一致,適用于特定的激活函數。
缺點
對于其他激活函數效果有限。
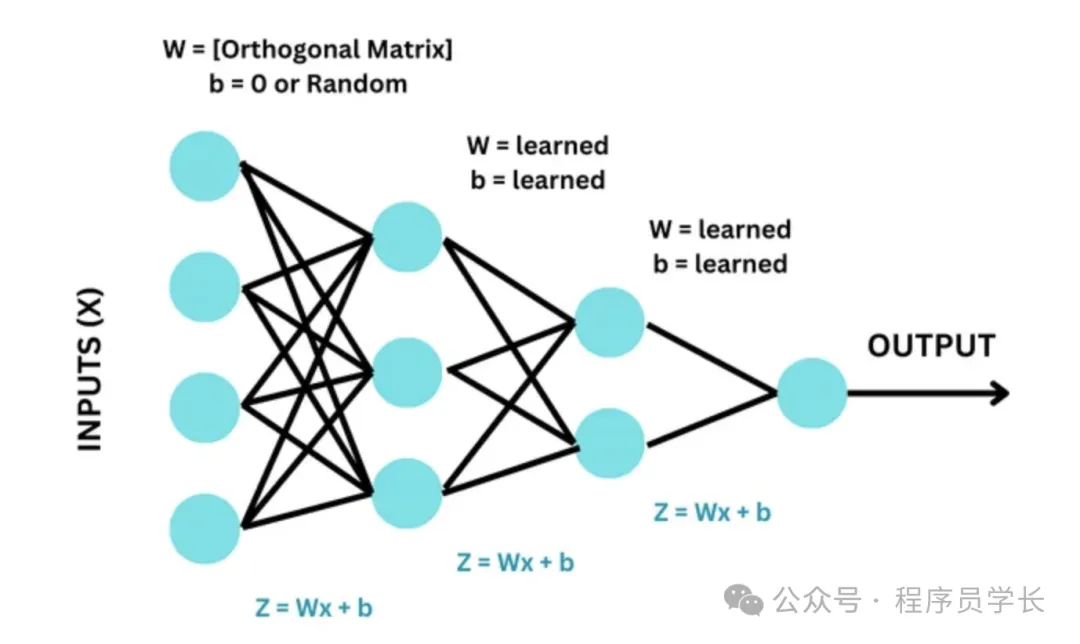
6.Orthogonal初始化(Orthogonal Initialization)
Orthogonal 初始化是將權重矩陣初始化為一個正交矩陣。
正交矩陣的特性使得其轉置矩陣也是其逆矩陣,從而在反向傳播中能夠很好地保持信號的流動。
優點
能有效避免梯度消失和梯度爆炸問題,特別適用于深度神經網絡。
缺點
計算復雜度較高,適用范圍有限。
7.Variance Scaling 初始化
Variance Scaling 初始化是一種基于方差縮放的權重初始化方法。
它是為了解決在深度網絡中,由于不當的權重初始化導致的梯度消失或梯度爆炸問題。
Variance Scaling 初始化通過縮放初始化權重的方差,使得每一層的輸出方差保持一致,從而穩定模型的訓練過程。
Variance Scaling 初始化通常使用以下公式定義:
其中:
- W 是初始化后的權重矩陣。
- 是當前層的輸入單元數(即輸入特征的數量)。
- 是一個可調參數,用于縮放權重的方差。常見的縮放參數有 1、2、 等。
- 表示均值為 0、方差為 的正態分布。
優點
- 通用性強,Variance Scaling 初始化是一種非常通用的初始化方法,可以適應不同的網絡結構和激活函數。
- 避免梯度消失/爆炸,通過合適的方差縮放,Variance Scaling 初始化能夠有效避免梯度消失或爆炸問題。
缺點
- 參數選擇復雜,需要根據具體的激活函數和網絡結構選擇合適的縮放因子,這增加了使用的復雜性。

























