譯者 | 劉濤

審校 | 重樓

控制理論是一門研究如何通過輸入信號使系統以期望方式運行的學科。

飛機、汽車、火車、電路及火箭等多種系統，都需要一個類似于大腦的核心控制單元或內部架構。

控制理論正是對這些復雜系統的控制架構進行深入研究的領域。

在本文中，我們提供了一個關于如何構建復雜系統架構的基礎指南，將探討如何運用控制理論，并借助Python編程語言來構建一個火箭控制系統。

你將深入了解以下內容：

• 火箭系統與烘焙蛋糕之間的趣味類比
• 簡化火箭控制原理：深入理解PID控制器
• 代碼示例：設計一個簡單的PID控制器
• 結論：非線性控制系統備注：本文假定火箭系統是時間不變的，即其運行軌跡不會隨時間發生改變。若要處理隨時間變化的動態特性，將不在本文的討論范圍之內。

一、火箭系統與烘焙蛋糕之間的趣味類比

什么是火箭控制系統

讓我們用一個烤蛋糕的比喻來解釋。設想你正在制作一個蛋糕，你的食譜提供了制作蛋糕所需的步驟和材料。

在這個類比中：

• 蛋糕代表火箭
• 食譜對應火箭的飛行計劃
• 烘焙師的操作則象征著火箭控制系統正如你通過調整烤箱溫度或攪拌時間來制作出最佳的蛋糕，火箭控制系統也會調整火箭的各項參數，確保其沿著預定軌道飛行并保持穩定。

為什么控制系統在編程中至關重要

理解控制系統可以幫助你在算法設計和系統思維方面變得更加熟練。

此外，它還允許你在反饋回路中調整過程，這在編程的眾多領域中都非常關鍵。

你主要會在以下軟件開發中應用控制理論和控制系統：

• 機器人與自動化領域：控制系統通過基于傳感器輸入的反饋回路，實現機器人的精確運動和自適應能力。
• 信號處理與通信領域：它們優化數據傳輸、錯誤校正和信號過濾，以確保通信的可靠性。
• 嵌入式系統與物聯網：控制系統負責管理設備與環境的交互，處理傳感器輸入，并高效地調整輸出。

如何創建一個火箭控制系統

以烤蛋糕的類比來闡述：

1. 選擇蛋糕與食譜：挑選一種簡單的控制策略，就如同選擇一份基礎的蛋糕食譜。PID控制器是常見的選擇，因其簡潔而高效。
2. 深入理解原料：對火箭的特性及其軌跡進行數學建模，這類似于深入研究食譜及其原料。這樣做可以幫助我們清晰地認識系統。
3. 準備初始原料：設定初始參數，這個過程類似于收集制作蛋糕所需的基本原料。
4. 混合與烘焙：對系統進行調整和測試，正如混合原料并進行烘焙的過程。這通常涉及到利用各種圖表來評估系統的穩定性和性能。
5. 添加后期修飾：對參數進行微調，以優化控制系統的效率，這就像為蛋糕添加后期的裝飾一樣。
6. 嚴格遵循食譜：將設計轉化為實際操作，這就像細致地遵循蛋糕食譜的每一步驟。

二、簡化火箭控制原理：深入理解PID控制器

一個簡單的控制系統：PID控制器

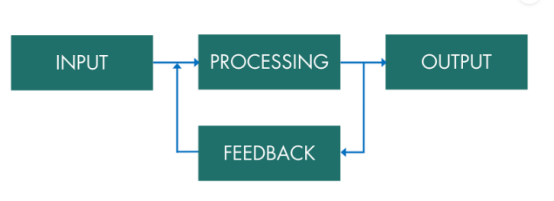控制系統圖示例（來源）

每個控制系統都配備有一個核心組件——控制器，以執行其運行指令。在眾多控制器中，PID控制器是最為常用的類型之一。它因其簡單性和高效性，在簡單控制系統中得到了廣泛的應用。

在以下代碼示例中，我們將采用PID控制器。選擇PID控制器的原因在于，它對于處理基礎控制任務來說，不僅易于實現，而且效果顯著。

在火箭控制系統中，PID控制器承擔著通過對比火箭的實際飛行位置與預定軌跡（即反饋環節）來不斷調整飛行路徑（即處理環節）的任務。

這一機制確保了火箭能夠精確地沿著預定軌道飛行，并最終準確抵達目的地。

PID控制器由三個關鍵部分組成，它們在系統的處理與反饋環節中協同作用：比例增益（Kp）、積分增益（Ki）以及微分增益（Kd）。

• 比例增益（Kp）：能夠對誤差進行即時反應，促使系統迅速響應，但有時會導致超調目標。
• 積分增益（Ki）：通過累積歷史誤差，逐漸進行修正，以消除系統中的任何殘余誤差。但是，若積分增益設置過高，可能會引發系統的不穩定性。
• 微分增益（Kd）：負責預測未來的誤差，有助于防止超調，并使得系統響應更加平緩。這三個環節的協同作用，生成一個精確的控制信號，進而調整火箭的飛行參數。這保證了系統的穩定運行、精確控制以及高效執行。
  通過PID控制器，我們能夠精確地操控推力和高度等輸入參數對火箭位置和速度的影響，確保火箭穩定飛行，并沿著預定的軌跡準確導航。

穩定性分析

設計PID控制器實質上是在設計一個穩定的控制系統。

將這種設計穩定控制系統的過程稱為穩定性分析。

穩定性分析的方法有很多，但在代碼示例中我們將主要使用以下三種：

• 根軌跡法：該方法可以直觀地展示系統的穩定性和響應性。
• 波德圖法：該方法可顯示系統的增益（gain）和相位裕度（phase margins）。
• 奈奎斯特圖法：該方法用于闡述系統的穩定性和潛在的振蕩情況。在這種情況下，增益和相位裕度這兩個概念表明了控制系統對變化的容忍度。
  增益裕度反映系統在不喪失穩定性前提下，增益可以增加到的最大程度。所謂增益，是指輸入信號被放大的程度，用以生成輸出信號。
  相位裕度則反映系統在不喪失穩定性的前提下，可以承受的最大延遲。在控制理論中，延遲指的是輸出響應對于輸入信號的滯后時間。
  這些分析為我們提供了如何調整Kp、Ki和Kd的參數，以確保PID控制器能夠有效地對火箭進行控制。

傳遞函數的需求：控制火箭和確定組件值

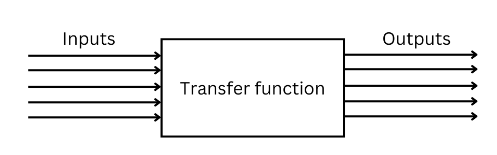
要實現對任何控制系統的精確控制，我們需要兩類傳遞函數：一類是理論傳遞函數，另一類是物理傳遞函數。

傳遞揭示了輸入信號如何通過數學關系轉換為輸出信號。

在當前的情境中，理論傳遞函數代表PID控制器的功能。

而物理系統傳遞函數則描述了系統中物理組件在實際工作環境中的動態特性和行為。

通過將這兩類傳遞函數相結合，我們能夠深入理解材料和組件值的實際表現，例如：

• 儲能電容器的參數值
• 用于精確數據測量和反饋的傳感器校準值
• 減震系統的彈簧剛度系數（Spring constants）
• 燃料和氧化劑儲存罐的額定工作壓力因此，PID控制器不僅是火箭控制系統的核心，還能夠指導我們確定火箭飛行所必需的各個組件的具體參數值。

工程師如何找到物理傳遞函數方程？

首先，我們必須明確火箭的用途和任務需求。

它是用于將衛星送入近地軌道或中地球軌道，還是用于執行月球探測等深空任務？

在明確了火箭的具體應用場景之后，我們可以通過數學建模和物理分析來推導出傳遞函數的物理方程。

實際上，存在一個專門的工程領域，稱為系統識別，其研究重點就是如何確定系統的傳遞函數。

接下來，讓我們探討如何針對控制系統，找到其物理傳遞函數的方法。

三、代碼示例：設計一個簡單的PID控制器

在接下來的代碼示例中，我們將構建一個用于火箭的簡易控制系統。

在深入代碼細節之前，我們先來討論一下分貝的概念。

分貝是一種采用對數尺度來衡量聲音強度的單位。在控制理論領域，分貝被用來以更直觀的方式在圖表上表示增益。

這樣，我們可以在可控范圍內看到更多大大小小的一系列增益值。

換句話說，通過對數尺度的增益，我們可以清晰地看到輸入信號在何種程度上被放大并轉化為輸出信號。

此外，我還將解釋根軌跡、波德圖和奈奎斯特圖如何輔助工程師進行系統的穩定性分析。

接下來，讓我們看看代碼—然后我們將逐塊對其進行詳細分析：

# Step 1: Import libraries
import matplotlib.pyplot as plt
import control as ctrl
# Step 2: Define a new rocket transfer function with poles closer to the imaginary axis

num = [10] 
den = [2, 2, 1] 
G = ctrl.TransferFunction(num, den)
# Step 3: Design a PID controller with new parameters
Kp = 5
Ki = 2
Kd = 1
C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0])
# Step 4: Applying the PID controller to the rocket transfer function
CL = ctrl.feedback(C * G, 1)
# Step 5: Plot Root Locus for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.root_locus(C * G, grid=True)
plt.title("Root Locus Plot (Closed-Loop)")
# Step 6: Plot Bode Plot for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.bode_plot(CL, dB=True, Hz=False, deg=True)
plt.suptitle("Bode Plot (Closed-Loop)", fnotallow=16)
# Step 7: Plot Nyquist Plot for Closed-Loop System
plt.figure(figsize=(10, 6))
ctrl.nyquist_plot(CL)
plt.title("Nyquist Plot (Closed-Loop)")
plt.show()

第1步：導入庫

import matplotlib.pyplot as plt
import control as ctrl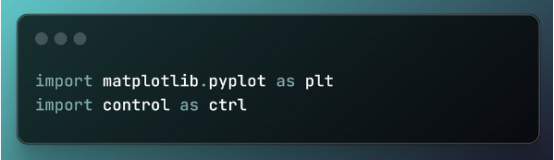

在這里我們導入兩個庫：

• matplotlib庫：用于創建各種類型可視化的繪圖庫
• 控制庫：用于分析和設計控制系統的庫

第2步：定義火箭系統的傳遞函數

num = [10] 
den = [2, 2, 1] 
G = ctrl.TransferFunction(num, den)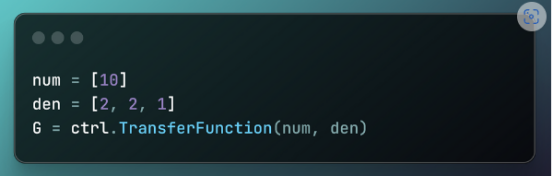

在這段代碼中，我們定義了物理系統的傳遞函數

1. num=[10]：將系統增益設置為10。
2. den=[2,2,1]：定義分母。
3. G = ctrl.transferFunction(num, cen)：構造傳遞函數。

以下是我們要用PID控制的傳遞函數：

<!DOCTYPE html>

Black-Scholes Equation
$$\frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} = rV - rS \frac{\partial V}{\partial S}$$

火箭傳遞函數

在本代碼示例中，所展示的火箭方程對應的傳遞函數被極大地簡化了。然而，在現實應用場景中，火箭的傳遞函數并非屬于時不變線性系統。實際上，它們往往表現出極高的復雜性，屬于典型的非線性系統。

第3步：設計具有新參數的PID控制器

Kp = 5
Ki = 2
Kd = 1
C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0])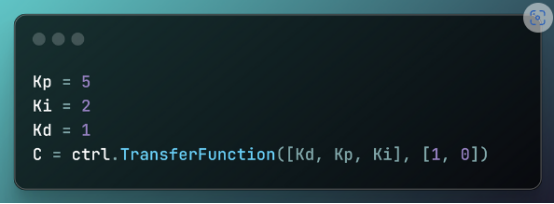

此代碼設置具有特定增益的PID控制器并創建傳遞函數：

• Kp = 5：將比例增益設置為5。
• Ki = 2：將積分增益設置為2。
• Kd = 1：將導數增益設置為1。
• C = ctrl.TransferFunction([Kd, Kp, Ki], [1, 0])：創建PID控制器的傳遞函數

第4步：將PID控制器應用于火箭傳遞函數

CL = ctrl.feedback(C * G, 1)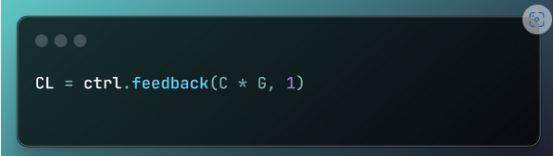

PID控制器在火箭傳遞函數中的應用

• C * G：表示將PID控制器C與系統G（即火箭）相乘，從而構成開環傳遞函數。該傳遞函數在沒有反饋機制介入的情況下，對系統的行為進行建模，其性能表現依賴于預先設定的參數配置。
• ctrl.feedback(C * G, 1)：此步驟通過施加反饋，并利用反饋信號來表征系統的行為，進而計算出閉環傳遞函數。這一過程使得系統能夠根據輸入信號自動調整，以實現誤差的自動糾正。
• CL：代表存儲生成的閉環系統模型，該模型通過反饋機制將控制器與火箭相結合，以維持所需的性能指標。該閉環系統模型可用于進一步的性能分析或仿真研究。

第5步：增益分析的根軌跡

在此代碼中：

plt.figure(figsize=(10, 6))
ctrl.root_locus(C * G, grid=True)
plt.title("Root Locus Plot (Closed-Loop)")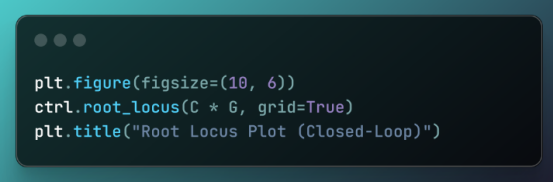

創建根軌跡圖

我們生成這個圖：

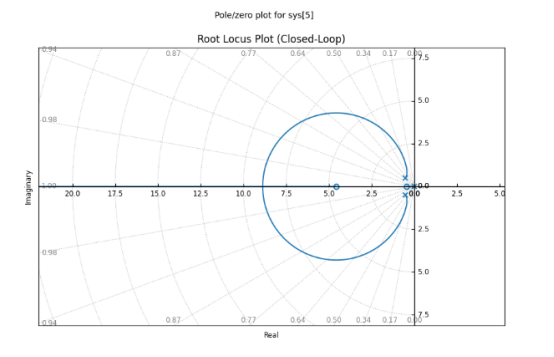簡單根軌跡圖

這是一幅根軌跡圖，它是工程師們為了研究控制系統穩定性而采用的一種分析工具。

圖中所示的十字標記，被稱作極點，其在根軌跡圖中的位置至關重要。

當極點位于圖的左側時，表明系統處于穩定狀態；反之，若極點位于右側，則意味著系統是不穩定的。

極點越偏向左側，系統在遭受干擾后恢復至正常狀態的速度越快，從而系統的穩定性越高。

然而，極點過度左移可能會導致系統產生過多的振蕩，其穩定性取決于極點的具體位置。

綜上所述，關鍵在于：

• 通過調整比例系數Kp、積分系數Ki和微分系數Kd，使極點盡可能地向左移動，而不會引發振蕩。然而，僅憑根軌跡圖并不能充分確保系統的穩定性。為此，我們還需借助波德圖和奈奎斯特圖進行分析。只有結合這些圖表，我們才能精確地確定火箭控制系統中PID控制器的最佳參數值。

第6步：穩定性分析的波德圖分析

在當前代碼中：

plt.figure(figsize=(10, 6))
ctrl.bode_plot(CL, dB=True, Hz=False, deg=True)
plt.suptitle("Bode Plot (Closed-Loop)", fnotallow=16)

創建波德圖

我們生成如下圖：

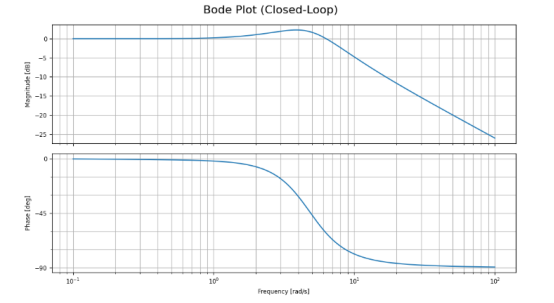簡單波德圖

波德圖的創制旨在輔助工程師深入掌握系統對變化的響應特性，以及其在不同工況下的穩定性能。

此外，波德圖亦能揭示系統的穩定狀態及其安全裕度（safety margins）。

以下，我們將探討波德圖的工作原理：

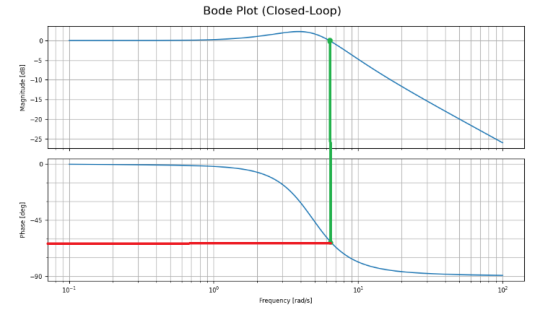波德圖細節

上述圖表中的上方圖像被稱為幅度圖，而下方圖像則稱為相位圖。

幅度圖用于衡量系統在各個頻率下的增益大小。較高的增益值表示系統具有更迅速且強烈的響應，這對于實現精確控制是有益的。

相位圖則用于測量系統在各個頻率下所引入的相位移。當增益降至零時，我們可以觀察到相位移的情況。

在此情形下，我們可以通過綠線確定增益為零的時刻，以及與紅線相對應的相位移，其數值大約為63度。

理想情況下，相位移的范圍應控制在30到60度之間，這一范圍能夠在系統的穩定性和響應速度之間取得平衡。

若相位移超過60度，系統將表現出極高的穩定性，但可能會降低系統對變化的響應速度。

綜上所述，通過對該圖表的分析，我們可以得出結論，該PID控制器是處于穩定狀態的。

第7步：用于穩定性分析的奈奎斯特圖

在以下代碼中：

plt.figure(figsize=(10, 6))
ctrl.nyquist_plot(CL)
plt.title("Nyquist Plot (Closed-Loop)")

創建奈奎斯特繪圖

我們生成如下圖：

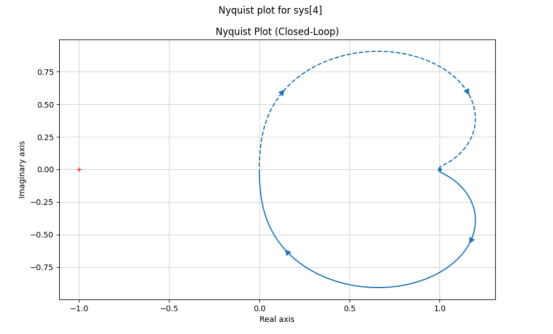奈奎斯特繪圖

奈奎斯特圖是一種輔助工程師迅速評估控制系統穩定性的工具。

其原理如下：

• 若在點（-1, 0）處不存在圍繞紅十字的封閉曲線，則表明系統是穩定的。
• 若在點（-1, 0）處存在圍繞紅十字的封閉曲線，且該曲線為順時針方向，則表明系統是不穩定的。從上圖來看，由于在紅十字周邊并沒有封閉曲線，因此可以判定該控制系統是穩定的。

火箭控制系統設計的最終階段

在完成PID控制系統的設計之后，我們可以利用諸如Simulink之類的工具來確定眾多組件所需的確切參數。

換句話說，在確定了最佳的PID控制器參數之后，便進入了確定火箭物理組件參數的階段。

這些參數包括：

• 控制電流的電阻器參數
• 儲能電容器的參數
• 管理電磁干擾的電感器參數
• 用于精確數據測量與反饋的傳感器校準參數
• 火箭機身及尾翼材料的強度與耐久性參數
• 伺服電機的扭矩與速度要求
• 減震系統的彈簧常數
• 燃料與氧化劑罐的額定壓力

得益于Simulink，我們能夠根據火箭的任務需求，獲得設計火箭所需的所有這些參數。

通過構建一個穩定的控制系統，并基于PID控制器來控制火箭的物理傳遞函數，我們能夠確定每個組件所需的所有關鍵參數。

結論：非線性控制系統

對于線性時不變系統(LTI)的優化，我們擁有多種方法：

1. 根軌跡法：通過調整系統極點來減少振蕩現象。
2. 波德圖分析：確保系統的相裕度和穩定性得以維持。
3. 奈奎斯特圖分析：確認系統的整體穩定性。

利用這些工具，我們可以構建出一個有效的控制系統。

然而，在這一過程中，最好采用諸如Ziegler-Nicholas方法類，以便更快速地確定最佳的PID控制器參數。

在本次研究中，我們以一個極為簡化的火箭系統作為對象進行探討。

在現實情況中，我們通常僅使用非線性工具，因為所有的火箭系統本質上都是非線性系統。

以自適應控制為例，控制系統會實時調整自身以應對不斷變化的環境條件。

另一個例子是Lyapunov方法。還是在以上情況下，它卻被用于穩定性分析，而非上述三種圖形分析。

盡管如此，構建這些控制系統的過程始終保持一致。本文詳細闡述了這一過程的工作原理，以及它是如何應用于線性時不變系統的。

https://github.com/tiagomonteiro0715/freecodecamp-my-articles-source-code

譯者介紹

劉濤，51CTO社區編輯，某大型央企系統上線檢測管控負責人。

原文標題：How to Build a Rocket Control System: Basic Control Theory with Python，作者：Tiago Monteiro