我們一起聊聊 C# 檢查曲線拐點與斜率變化
在數(shù)據(jù)分析和可視化過程中,識別曲線的拐點(或趾點)是非常重要的。這些點標(biāo)志著趨勢的變化,可以提供關(guān)于數(shù)據(jù)行為和模式的信息。在這篇文章中,我們將探索如何在C#中實現(xiàn)拐點檢測,使用簡單的斜率(或?qū)?shù))計算進(jìn)行基礎(chǔ)分析。
什么是拐點?
拐點是函數(shù)或曲線圖中,曲線的凹凸性改變的位置。例如,從上升轉(zhuǎn)為下降或從下降轉(zhuǎn)為上升時,通常會出現(xiàn)拐點。在數(shù)學(xué)上,這可以通過分析函數(shù)導(dǎo)數(shù)的符號變化來識別。
應(yīng)用場景
市場分析
在股票市場或其他金融市場中,價格走勢往往會在拐點處發(fā)生趨勢改變。通過檢測這些拐點,交易員可以更好地預(yù)測市場方向,制定買入或賣出的決策。此外,價格指數(shù)的數(shù)據(jù)分析可以幫助識別經(jīng)濟(jì)周期中的重要轉(zhuǎn)折點。
醫(yī)療診斷
在醫(yī)療數(shù)據(jù)分析中,拐點檢測可以用于分析生理曲線,如心電圖、腦電圖或其他生物信號。識別拐點有助于檢測異常模式,例如心律不齊或突發(fā)波形的識別,從而為醫(yī)生提供診斷支持。
產(chǎn)品性能分析
在產(chǎn)品測試和性能評估中,數(shù)據(jù)中出現(xiàn)的拐點可以指示產(chǎn)品特性的變化,例如壓力測試中材料性質(zhì)的改變。識別這些拐點有助于在質(zhì)量控制過程中進(jìn)行早期故障檢測,并指導(dǎo)產(chǎn)品改進(jìn)。
氣候變化研究
在氣象數(shù)據(jù)或氣候模型中,識別長期趨勢中的拐點可以幫助研究人員了解氣候變化的模式,如溫度上升或下降的起始點。這對制定應(yīng)對氣候變化的政策和措施具有重要意義。
使用C#進(jìn)行拐點檢測
準(zhǔn)備工作
- 引用 ScottPlot (或任何其他必要的繪圖庫),以便可視化分析結(jié)果。如果使用ScottPlot,可以通過NuGet安裝。
- 例子中安裝的是ScottPlot.Winform 5.0以上版本
示例
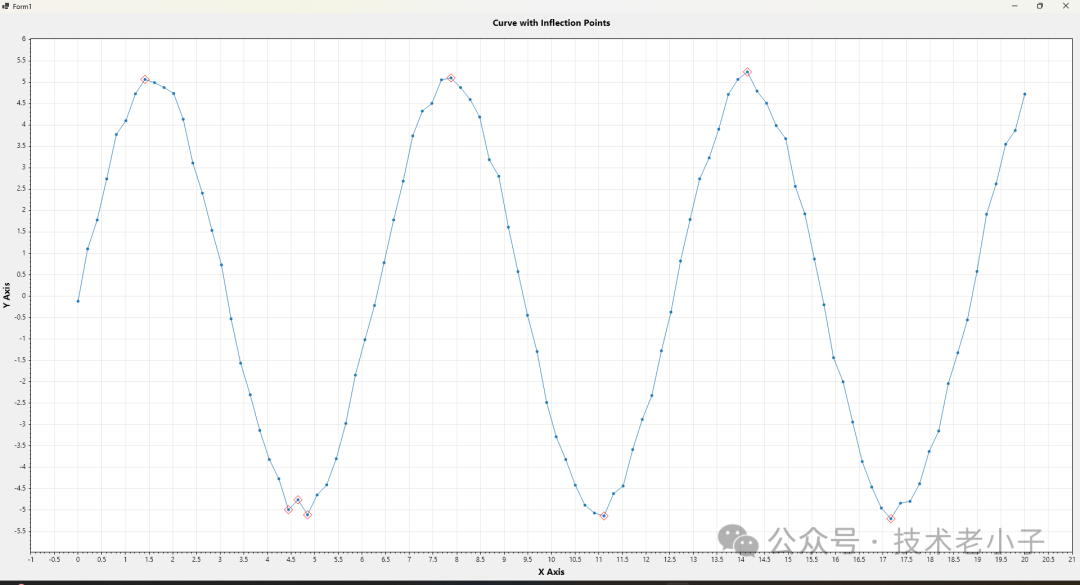 圖片
圖片
我們將通過計算相鄰數(shù)據(jù)點間的差值來近似曲線的導(dǎo)數(shù),當(dāng)這些差值(斜率)發(fā)生符號變化時,就標(biāo)記為一個拐點。
Random rand = new Random();
double RandomNoise()
{
return rand.NextDouble() * 0.5 - 0.25; // 生成 -0.25 到 0.25 之間的噪聲
}
private void Form1_Load(object sender, EventArgs e)
{
// 設(shè)置數(shù)據(jù)點數(shù)量和范圍
int pointCount = 100; // 數(shù)據(jù)點的數(shù)量
double xStart = 0;
double xEnd = 20;
// 生成x和y數(shù)據(jù)
double[] xs = Enumerable.Range(0, pointCount).Select(i => xStart + (xEnd - xStart) * i / (pointCount - 1)).ToArray();
double[] ys = xs.Select(x => Math.Sin(x) * 5 + RandomNoise()).ToArray();
// 檢測拐點
List<int> inflectionPointIndices = DetectInflectionPoints(ys.ToList());
formsPlot1.Plot.Add.Scatter(xs, ys);
// 標(biāo)記拐點
float inflectionPointMarkerSize = 15.0f; // 設(shè)置拐點的標(biāo)記大小
foreach (var idx in inflectionPointIndices)
{
formsPlot1.Plot.Add.Markers(
new double[] { xs[idx] },
new double[] { ys[idx] },
color: Colors.Red,
shape: MarkerShape.OpenDiamond,
size: inflectionPointMarkerSize
);
}
// 添加圖例
formsPlot1.Plot.Legend.FontSize = 12;
// 顯示圖表
formsPlot1.Plot.Title("Curve with Inflection Points");
formsPlot1.Plot.YLabel("Y Axis");
formsPlot1.Plot.XLabel("X Axis");
formsPlot1.Refresh();
}
List<int> DetectInflectionPoints(List<double> data)
{
List<int> inflectionPoints = new List<int>();
List<double> firstDerivatives = new List<double>();
for (int i = 1; i < data.Count; i++)
{
firstDerivatives.Add(data[i] - data[i - 1]);
}
for (int i = 1; i < firstDerivatives.Count; i++)
{
if (firstDerivatives[i] * firstDerivatives[i - 1] < 0)
{
inflectionPoints.Add(i);
}
}
return inflectionPoints;
}- if (firstDerivatives[i] * firstDerivatives[i - 1] < 0):
- 檢查當(dāng)前差分值與前一個差分值的乘積是否小于0。
- 如果是,這意味著由上一個點到當(dāng)前點的斜率發(fā)生了符號變化,意味著經(jīng)過了一個拐點。
拐點檢測背后原理
- 一階差分:
這是一個簡單的近似導(dǎo)數(shù),用于估算函數(shù)在離散點上的斜率變化。
- 乘積符號變化:
如果相鄰兩個一階差分的乘積小于零,說明這兩個差分之間發(fā)生了正負(fù)變化,這通常是一個拐點的特征。
總結(jié)
識別曲線的拐點對于分析數(shù)據(jù)中的趨勢變化極為重要。在C#中,通過計算數(shù)據(jù)點之間的差異,我們能夠有效地識別這些拐點,并幫助我們更好地理解數(shù)據(jù)的變化模式。通過可視化結(jié)果,我們不僅可以驗證計算的準(zhǔn)確性,還能更直觀地展示數(shù)據(jù)中的關(guān)鍵點。
這種方法非常基礎(chǔ),適合簡單的數(shù)據(jù)集和初步分析。復(fù)雜數(shù)據(jù)或更精確的分析可能需要采用更高級的數(shù)學(xué)工具和算法。











































