使用Python實(shí)現(xiàn)基于矩陣分解的長期事件(MFLEs)時間序列分析
在現(xiàn)代數(shù)據(jù)分析領(lǐng)域,時間序列數(shù)據(jù)的處理和預(yù)測一直是一個具有挑戰(zhàn)性的問題。隨著物聯(lián)網(wǎng)設(shè)備、金融交易系統(tǒng)和工業(yè)傳感器的普及,我們面臨著越來越多的高維時間序列數(shù)據(jù)。這些數(shù)據(jù)不僅維度高,而且往往包含復(fù)雜的時間依賴關(guān)系和潛在模式。傳統(tǒng)的時間序列分析方法如移動平均等,在處理此類數(shù)據(jù)時往往顯得力不從心。

基于矩陣分解的長期事件(Matrix Factorization for Long-term Events, MFLEs)分析技術(shù)應(yīng)運(yùn)而生。這種方法結(jié)合了矩陣分解的降維能力和時間序列分析的特性,為處理大規(guī)模時間序列數(shù)據(jù)提供了一個有效的解決方案。
核心概念
矩陣分解
矩陣分解(Matrix Factorization)是將一個矩陣分解為多個基礎(chǔ)矩陣的乘積的過程。在時間序列分析中,最常用的是奇異值分解(Singular Value Decomposition, SVD)。SVD可以將原始矩陣 A 分解為:
A = USV^T
其中:
- U 和 V 是正交矩陣
- S 是對角矩陣,對角線上的元素稱為奇異值
潛在變量與潛在特征
- 潛在變量(Latent Variables):指數(shù)據(jù)中無法直接觀測但實(shí)際存在的變量,它們往往是多個可觀測變量的綜合表現(xiàn)。
- 潛在特征(Latent Features):通過矩陣分解得到的低維表示,它們是潛在變量在數(shù)學(xué)上的具體體現(xiàn)。每個潛在特征可能代表多個原始特征的組合。
維度降低在時間序列分析中的意義
維度降低(Dimensionality Reduction)在時間序列分析中具有多重意義:
計(jì)算效率:
- 原始維度下的計(jì)算復(fù)雜度:O(n^3),其中n為特征數(shù)量
- 降維后的計(jì)算復(fù)雜度:O(k^3),其中k為降低后的維度數(shù),通常k << n
噪聲過濾:
- 較小的奇異值通常對應(yīng)噪聲分量
- 保留主要奇異值可以實(shí)現(xiàn)數(shù)據(jù)去噪
模式提取:
- 幫助發(fā)現(xiàn)時間序列中的主要趨勢和季節(jié)性模式
- 便于識別多個時間序列之間的相關(guān)性
主成分分析(PCA)與MFLE的關(guān)系
主成分分析(Principal Component Analysis, PCA)是一種經(jīng)典的降維方法,而MFLE可以看作是PCA在時間序列領(lǐng)域的擴(kuò)展應(yīng)用。與PCA相比,MFLE具有以下特點(diǎn):
- 時間敏感性:考慮數(shù)據(jù)點(diǎn)之間的時間依賴關(guān)系
- 預(yù)測能力:能夠基于歷史模式進(jìn)行預(yù)測
- 多序列建模:可以同時處理多個相關(guān)的時間序列
MFLE的數(shù)學(xué)基礎(chǔ)
MFLE的核心思想是將時間序列數(shù)據(jù)矩陣 X ∈ ?^(m×n) 分解為兩個低維矩陣的乘積:
X ≈ WH
其中:
- W ∈ ?^(m×k) 表示基矩陣(basis matrix)
- H ∈ ?^(k×n) 表示編碼矩陣(encoding matrix)
- k 是潛在特征的數(shù)量,通常 k << min(m,n)
這種分解通過最小化以下目標(biāo)函數(shù)來實(shí)現(xiàn):
min ||X - WH||F^2 + λ(||W||F^2 + ||H||_F^2)
其中:
- ||·||_F 表示Frobenius范數(shù)
- λ 是正則化參數(shù),用于防止過擬合
長期事件(MFLEs)技術(shù)實(shí)現(xiàn)
數(shù)據(jù)準(zhǔn)備與預(yù)處理
import numpy as np
import pandas as pd
from sklearn.decomposition import TruncatedSVD
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 生成合成數(shù)據(jù)
np.random.seed(42)
n_series = 100 # 時間序列的數(shù)量
n_timepoints = 50 # 時間點(diǎn)的數(shù)量
# 模擬數(shù)據(jù)矩陣(行:時間序列,列:時間點(diǎn))
data_matrix = np.random.rand(n_series, n_timepoints)
df = pd.DataFrame(data_matrix)
print(df.head())在這個實(shí)現(xiàn)中,我們選擇了100個時間序列,每個序列包含50個時間點(diǎn)。這些參數(shù)的選擇基于以下考慮:
- n_series = 100:提供足夠的樣本量以捕獲不同的模式
- n_timepoints = 50:足夠長以體現(xiàn)時間序列的特性,又不會造成過大的計(jì)算負(fù)擔(dān)
矩陣分解實(shí)現(xiàn)
svd = TruncatedSVD(n_components=10) # 降至10個潛在特征
latent_features = svd.fit_transform(data_matrix)
# 重構(gòu)時間序列
reconstructed_matrix = svd.inverse_transform(latent_features)關(guān)鍵參數(shù)說明:
n_components = 10
- 選擇理由:通常選擇能解釋80-90%方差的特征數(shù)量
- 計(jì)算成本:與特征數(shù)量的三次方成正比
- 最佳實(shí)踐:可以通過explained_variance_ratio_確定
截斷SVD(TruncatedSVD)
- 優(yōu)勢:內(nèi)存效率高,計(jì)算速度快
- 適用場景:大規(guī)模稀疏矩陣
- 數(shù)學(xué)原理:只計(jì)算前k個最大奇異值
預(yù)測模型構(gòu)建
# 準(zhǔn)備訓(xùn)練和測試數(shù)據(jù)集
X = latent_features[:, :-1]
y = latent_features[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 訓(xùn)練回歸模型
model = LinearRegression()
model.fit(X_train, y_train)
# 進(jìn)行預(yù)測
y_pred = model.predict(X_test)模型選擇考慮:
線性回歸
- 優(yōu)勢:計(jì)算效率高,可解釋性強(qiáng)
- 局限:僅能捕獲線性關(guān)系
- 適用場景:潛在特征間的關(guān)系較為簡單時
數(shù)據(jù)分割(test_size=0.2)
- 標(biāo)準(zhǔn)做法:留出20%作為測試集
- 注意事項(xiàng):需要考慮時間序列的連續(xù)性
可視化分析
單序列重構(gòu)效果分析
"""
原始與重構(gòu)時間序列的對比
"""
import matplotlib.pyplot as plt
# 繪制原始與重構(gòu)時間序列的對比圖
series_idx = 0 # 選擇特定的時間序列
plt.figure(figsize=(10, 6))
plt.plot(data_matrix[series_idx, :], label="Original", marker="o")
plt.plot(reconstructed_matrix[series_idx, :], label="Reconstructed", linestyle="--")
plt.title("MFLE: Original vs Reconstructed Time Series")
plt.xlabel("Time")
plt.ylabel("Values")
plt.legend()
plt.grid()
plt.show()
可視化結(jié)果解讀:
重構(gòu)質(zhì)量評估
- 曲線吻合度反映了模型捕獲主要模式的能力
- 偏差主要出現(xiàn)在局部波動處
- 整體趨勢被很好地保留
噪聲過濾效果
- 重構(gòu)序列更平滑
- 去除了高頻波動
- 保留了主要趨勢
綜合性能評估
import matplotlib.pyplot as plt
import seaborn as sns
# 設(shè)置繪圖
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Time Series Analysis and Prediction', fontsize=16)
# 1. 原始數(shù)據(jù)與重構(gòu)數(shù)據(jù)對比(第一個時間序列)
axes[0, 0].plot(data_matrix[:1].T, 'b-', alpha=0.5, label='Original')
axes[0, 0].plot(reconstructed_matrix[:1].T, color="Red", label='Reconstructed')
axes[0, 0].set_title('Original vs. Reconstructed Data')
axes[0, 0].set_xlabel('Time Points')
axes[0, 0].set_ylabel('Value')
axes[0, 0].legend()
# 2. 解釋方差比
explained_variance_ratio = svd.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
axes[0, 1].plot(range(1, len(explained_variance_ratio) + 1), cumulative_variance_ratio, 'bo-')
axes[0, 1].set_title('Cumulative Explained Variance Ratio')
axes[0, 1].set_xlabel('Number of Components')
axes[0, 1].set_ylabel('Cumulative Explained Variance Ratio')
axes[0, 1].set_ylim([0, 1])
# 3. 實(shí)際值與預(yù)測值對比
axes[1, 0].scatter(y_test, y_pred)
axes[1, 0].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
axes[1, 0].set_title('Actual vs. Predicted Values')
axes[1, 0].set_xlabel('Actual Values')
axes[1, 0].set_ylabel('Predicted Values')
# 4. 殘差圖
residuals = y_test - y_pred
axes[1, 1].scatter(y_pred, residuals)
axes[1, 1].axhline(y=0, color='r', linestyle='--')
axes[1, 1].set_title('Residual Plot')
axes[1, 1].set_xlabel('Predicted Values')
axes[1, 1].set_ylabel('Residuals')
plt.tight_layout()
plt.show()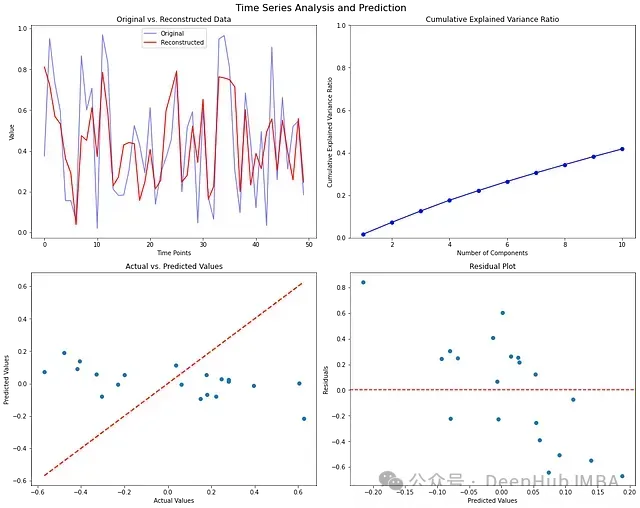
多圖表分析:
解釋方差比分析
- 累積方差比反映了信息保留程度
- 拐點(diǎn)可用于確定最優(yōu)特征數(shù)量
- 通常在90%處截斷較為合理
預(yù)測性能評估
- 散點(diǎn)圖集中在對角線附近表示預(yù)測準(zhǔn)確
- 殘差圖用于檢測系統(tǒng)性偏差
- 殘差的分布特征反映了模型假設(shè)的合理性
與其他時間序列分析方法對比
傳統(tǒng)統(tǒng)計(jì)方法對比
ARIMA模型
- 優(yōu)勢:適合單變量時間序列,模型解釋性強(qiáng)
- 局限:難以處理高維數(shù)據(jù),計(jì)算復(fù)雜度高
- 對比:MFLE在處理多變量時更有效率
指數(shù)平滑法
- 優(yōu)勢:計(jì)算簡單,適合短期預(yù)測
- 局限:無法捕獲復(fù)雜的時間依賴關(guān)系
- 對比:MFLE能夠發(fā)現(xiàn)更深層的數(shù)據(jù)結(jié)構(gòu)
深度學(xué)習(xí)方法對比
LSTM網(wǎng)絡(luò)
- 優(yōu)勢:能夠?qū)W習(xí)復(fù)雜的時序依賴
- 局限:需要大量訓(xùn)練數(shù)據(jù),計(jì)算資源消耗大
- 對比:MFLE在計(jì)算效率和可解釋性方面更具優(yōu)勢
時序自編碼器
- 優(yōu)勢:能夠?qū)W習(xí)非線性特征
- 局限:模型復(fù)雜,訓(xùn)練不穩(wěn)定
- 對比:MFLE提供了更簡單且可解釋的解決方案
總結(jié)
時間序列數(shù)據(jù)的高維特性和復(fù)雜的時間依賴關(guān)系使其分析具有挑戰(zhàn)性。MFLE通過結(jié)合矩陣分解和時間序列分析的優(yōu)勢,為這類問題提供了一個有效的解決方案。
通過對MFLE的深入理解和合理應(yīng)用,可以在眾多實(shí)際場景中獲得良好的分析效果。未來隨著算法的改進(jìn)和計(jì)算能力的提升,MFLE的應(yīng)用范圍將進(jìn)一步擴(kuò)大。