金融波動率的多模型建模研究:GARCH族與HAR模型的Python實現與對比分析
金融資產波動率建模在現代金融工程中具有重要地位,其應用涵蓋風險管理、衍生品定價和投資組合優化等核心領域。本文著重探討三種主流波動率建模方法:廣義自回歸條件異方差模型(GARCH)、Glosten-Jagannathan-Runkle-GARCH模型(GJR-GARCH)以及異質自回歸模型(HAR)。本文將系統闡述這些模型的理論基礎,并基于標準普爾500指數ETF(SPY)的實際交易數據進行實證分析。
理論基礎
1、 GARCH模型
GARCH(1,1)模型由Bollerslev于1986年提出,該模型有效捕捉了金融時間序列中的波動率聚類特征。模型的數學表達式為:
r_t = μ + εtεt = σt * z_tσ2t = ω + α * ε2(t-1) + β * σ2(t-1)
其中各參數定義如下:
- r_t 表示t時刻的資產收益率
- μ 表示條件均值
- εt_ 表示隨機擾動項
- σt_ 表示條件波動率
- z_t 表示服從標準正態分布的隨機變量
- ω, α, β 為待估計參數集
該模型的核心特征在于:當前條件方差依賴于前期的隨機擾動項平方(α項)和前期條件方差(β項)。模型的波動率持續性由α + β之和度量,該值通常接近但嚴格小于1,以確保過程的平穩性。
2、GJR-GARCH模型
GJR-GARCH模型由Glosten、Jagannathan和Runkle于1993年提出,是對標準GARCH模型的重要擴展。該模型通過引入杠桿效應項,刻畫了金融市場中負向沖擊對波動率的非對稱影響。模型表達式為:
σ2t = ω + α * ε2(t-1) + γ * I(t-1) * ε2(t-1) + β * σ2_(t-1)
其中:
- I(t-1)_ 為示性函數,當ε_(t-1) < 0時取值為1,其他情況為0
- γ 為杠桿效應系數,用于捕捉負向收益率沖擊的額外影響
通過引入γ參數,模型能夠有效區分正負向市場信息對波動率的差異化影響,這一特性使其在股票市場波動率建模中表現出較強的實證效果,因為市場下跌通常會引發比上漲更顯著的波動率反應。
3、HAR模型
HAR(異質自回歸)模型由Corsi于2009年提出,該模型采用創新性的方法,通過整合不同時間尺度的波動率信息直接對已實現波動率進行建模。模型的基本形式為:
RV_t+1 = β? + βd * RV_t + βw * RV_t^w + βm * RV_t^m + εt+1
其中各變量定義如下:
- RV_t 代表日度已實現波動率
- RV_t^w 代表周度已實現波動率的算術平均值
- RV_t^m 代表月度已實現波動率的算術平均值
- β 系數集合反映了不同時間尺度波動率的邊際貢獻
實證分析與代碼實現
本節詳細闡述三種波動率模型的Python實現過程:
數據預處理
def get_spy_data():
"""獲取SPY指數近五年交易數據"""
end_date = datetime.now()
start_date = end_date - timedelta(days=5*365)
spy = yf.download('SPY', start=start_date, end=end_date)
return spy
def calculate_returns(prices):
"""計算連續復利收益率"""
return 100 * np.log(prices / prices.shift(1))本文采用對數收益率進行建模,這種處理方式具有兩個主要優勢:對數收益率具有可加性;對數收益率的分布通常更接近正態分布,這有利于后續的統計推斷。
GARCH模型估計
def fit_garch(returns):
"""估計GARCH(1,1)模型參數"""
model = arch_model(returns, vol='Garch', p=1, q=1)
results = model.fit(disp='off')
return resultsGARCH模型的參數估計采用arch計量經濟學庫實現,該庫基于最大似然估計方法提供了高效的參數估計功能。在實證研究中,GARCH(1,1)規范通常能夠充分捕捉金融時間序列的波動率動態特征。
GJR-GARCH模型估計
def fit_gjr_garch(returns):
"""估計GJR-GARCH(1,1)模型參數"""
model = arch_model(returns, p=1, o=1, q=1, dist='studentst')
results = model.fit(disp='off')
return resultsGJR-GARCH模型的實現引入了非對稱項參數(o=1),并采用學生t分布來更好地擬合金融收益率分布的尾部特征。模型自動包含了負向收益的示性函數處理機制。
HAR模型
def calculate_har_volatility(returns, lookback=22):
"""構建HAR模型并估計已實現波動率"""
rv = returns**2 # 計算日度已實現方差
# 構造不同時間尺度的HAR組件
rv_d = pd.Series(rv)
rv_w = rv.rolling(window=5).mean() # 構造周度波動率分量
rv_m = rv.rolling(window=22).mean() # 構造月度波動率分量
# 生成預測變量矩陣
X = pd.DataFrame({
'rv_d': rv_d.shift(1),
'rv_w': rv_w.shift(1),
'rv_m': rv_m.shift(1)
})
# 處理缺失值
y = rv[lookback:]
X = X[lookback:]
# 應用OLS方法進行參數估計
X = X.fillna(0)
beta = np.linalg.pinv(X) @ y
# 計算波動率預測值
har_vol = np.sqrt(252 * (X @ beta)) # 轉換為年化波動率
return har_volHAR模型的實現過程包含以下關鍵步驟:
- 基于收益率平方計算日度已實現方差
- 構造周度(5個交易日)和月度(22個交易日)波動率分量
- 構建滯后預測變量矩陣
- 采用普通最小二乘法進行參數估計
- 生成波動率預測序列
模型性能比較與可視化
我們還開發了專門的可視化模塊用于模型性能對比分析:
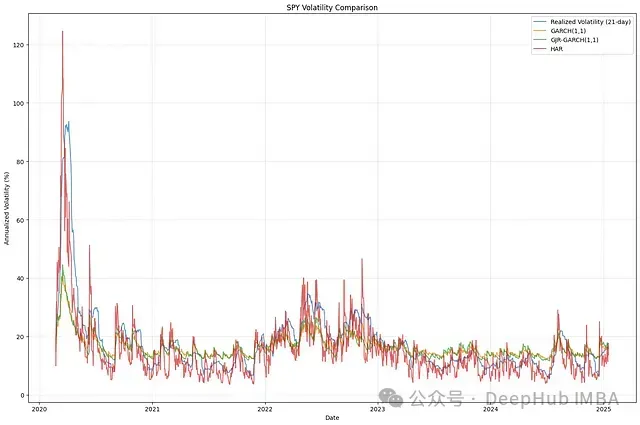
def plot_volatility_comparison(spy_data, garch_vol, gjr_vol, har_vol):
"""構建波動率模型比較圖"""
plt.figure(figsize=(15, 10))
# 計算歷史已實現波動率(21日滾動)
realized_vol = np.sqrt(252) * spy_data['Returns'].rolling(window=21).std()
# 統一時間序列索引
common_index = realized_vol.index.intersection(har_vol.index)
realized_vol = realized_vol[common_index]
garch_vol = garch_vol[common_index]
gjr_vol = gjr_vol[common_index]
har_vol = har_vol[common_index]
# 繪制各模型波動率序列
plt.plot(common_index, realized_vol, label='Realized Volatility (21-day)', alpha=0.7)
plt.plot(common_index, garch_vol, label='GARCH(1,1)', alpha=0.7)
plt.plot(common_index, gjr_vol, label='GJR-GARCH(1,1)', alpha=0.7)
plt.plot(common_index, har_vol, label='HAR', alpha=0.7)該可視化工具能夠直觀展示各模型對市場波動率的刻畫能力及其動態特征。
模型適用性分析
各模型在實證應用中表現出不同的優勢特征:
GARCH(1,1)模型:
- 模型結構簡潔,具有較強的穩健性
- 能夠有效捕捉波動率聚類現象
- 在金融業界獲得廣泛應用
GJR-GARCH模型:
- 較好地刻畫了波動率的非對稱響應特征
- 特別適用于股票市場波動率建模
- 在市場劇烈波動期間展現出較強的擬合優勢
HAR模型:
- 有效捕捉波動率的長期記憶特性
- 模型結構具有清晰的經濟學解釋
- 在高頻數據建模中表現突出
總結
波動率建模是金融風險管理中的關鍵環節。GARCH族模型基于嚴謹的統計理論基礎,能夠有效刻畫金融收益率的典型特征;而HAR模型則提供了一種直觀且實用的建模思路,在實證研究中展現出良好的預測性能。
本文通過Python實現展示了這些模型在實際市場數據中的應用方法,為更深入的金融計量分析和風險管理研究提供了實踐基礎。



































